2.3 函数奇偶性、周期性教学设计(表格式)——2026届高三数学一轮复习
文档属性
| 名称 | 2.3 函数奇偶性、周期性教学设计(表格式)——2026届高三数学一轮复习 | 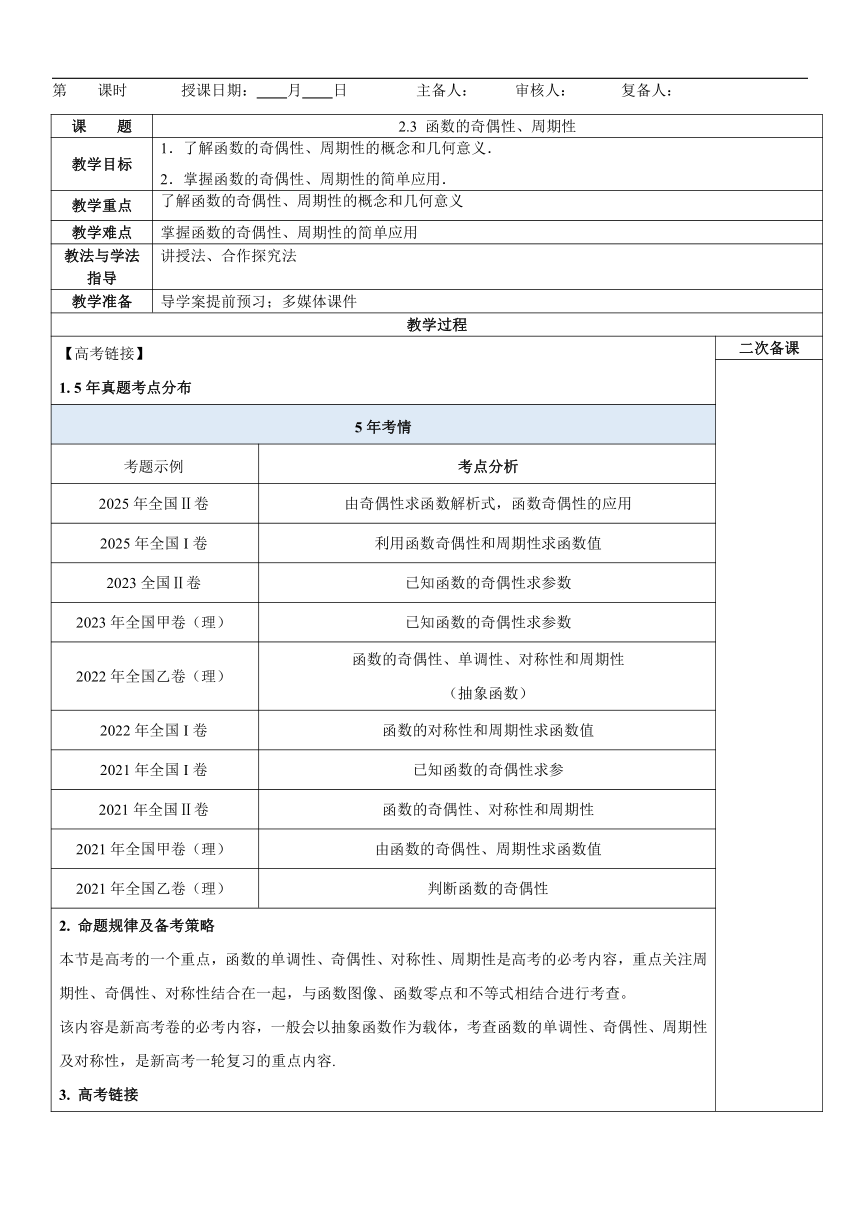 | |
| 格式 | docx | ||
| 文件大小 | 174.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-29 11:29:21 | ||
图片预览


文档简介
第 课时 授课日期: 月 日 主备人: 审核人: 复备人:
课 题 2.3 函数的奇偶性、周期性
教学目标 1.了解函数的奇偶性、周期性的概念和几何意义. 2.掌握函数的奇偶性、周期性的简单应用.
教学重点 了解函数的奇偶性、周期性的概念和几何意义
教学难点 掌握函数的奇偶性、周期性的简单应用
教法与学法指导 讲授法、合作探究法
教学准备 导学案提前预习;多媒体课件
教学过程
【高考链接】 1. 5年真题考点分布 5年考情考题示例考点分析2025年全国Ⅱ卷由奇偶性求函数解析式,函数奇偶性的应用2025年全国I卷利用函数奇偶性和周期性求函数值2023全国Ⅱ卷已知函数的奇偶性求参数2023年全国甲卷(理)已知函数的奇偶性求参数2022年全国乙卷(理)函数的奇偶性、单调性、对称性和周期性 (抽象函数)2022年全国I卷函数的对称性和周期性求函数值2021年全国I卷已知函数的奇偶性求参2021年全国Ⅱ卷函数的奇偶性、对称性和周期性2021年全国甲卷(理)由函数的奇偶性、周期性求函数值2021年全国乙卷(理)判断函数的奇偶性
命题规律及备考策略 本节是高考的一个重点,函数的单调性、奇偶性、对称性、周期性是高考的必考内容,重点关注周期性、奇偶性、对称性结合在一起,与函数图像、函数零点和不等式相结合进行考查。 该内容是新高考卷的必考内容,一般会以抽象函数作为载体,考查函数的单调性、奇偶性、周期性及对称性,是新高考一轮复习的重点内容. 高考链接 1.(2024·天津·高考真题)下列函数是偶函数的是( ) A. B. C. D. 2.(2024·上海·高考真题)已知,,且是奇函数,则 . 3.(2023·全国甲卷·高考真题)若为偶函数,则 . 4.(2023·全国乙卷·高考真题)已知是偶函数,则( ) A. B. C.1 D.2 5.(2023·全国新Ⅱ卷·高考真题)若为偶函数,则( ). A. B.0 C. D.1 6.(2022·全国乙卷·高考真题)若是奇函数,则 , . 7.(2021·全国甲卷·高考真题)设是定义域为R的奇函数,且.若,则( )A. B. C. D. 4.导入新课 1.函数的奇偶性 奇偶性定义图象特点偶函数一般地,设函数f(x)的定义域为D,如果 x∈D,都有-x∈D,且f(-x)=f(x),那么函数f(x)就叫做偶函数关于y轴对称奇函数一般地,设函数f(x)的定义域为D,如果 x∈D,都有-x∈D,且f(-x)=-f(x),那么函数f(x)就叫做奇函数关于原点对称
2.函数的周期性 (1)周期函数:一般地,设函数f(x)的定义域为D,如果存在一个非零常数T,使得对每一个x∈D都有x+T∈D,且f(x+T)=f(x),那么函数y=f(x)就叫做周期函数,非零常数T叫做这个函数的周期. (2)最小正周期:如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期. 重点结论 1.奇函数在关于原点对称的区间上具有相同的单调性;偶函数在关于原点对称的区间上具有相反的单调性. 2.函数周期性常用结论 对f(x)定义域内任意自变量的值x: (1)若f(x+a)=-f(x),则T=2a(a>0). (2)若f(x+a)=,则T=2a(a>0). 3.判断函数奇偶性的方法 (1)定义法 (2)图象法 (3)性质法 在公共定义域内有:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇. 注意:函数定义域关于原点对称是函数具有奇偶性的前提条件. 4.函数奇偶性的应用 (1)求函数值或参数的取值,求解的关键在于借助奇偶性转化为求已知区间上的函数值,或得到关于参数的恒等式,利用方程思想求参数的值. (2)比较大小,利用奇偶性把不在同一单调区间上的两个或多个自变量的函数值转化到同一单调区间上,进而利用其单调性比较大小. (3)解抽象函数不等式,先把不等式转化为f(g(x))>f(h(x))的形式,利用单调性把符号“f”脱掉,得到具体的不等式(组). 考点1 函数奇偶性的判断 【例1】 判断下列函数的奇偶性: (1)f(x)=+;(2)f(x)=(3)f(x)=log2(x+). 【对点训练1】 (1)(2024·天津卷)下列函数是偶函数的是( ) A.f(x)= B.f(x)= C.f(x)= D.f(x)= (2)已知f(x)为R上的奇函数,g(x)为R上的偶函数,且g(x)≠0,则下列说法正确的是( ) A.f(x)+g(x)为R上的奇函数 B.f(x)-g(x)为R上的偶函数 C.为R上的偶函数 D.|f(x)g(x)|为R上的偶函数 考点2 函数奇偶性的应用 命题角度1 利用函数的奇偶性求值(解析式) 【例2】 (1)若函数f(x)=是奇函数,则实数a=( ) A.0 B.-1 C.1 D.±1 (2)已知函数f(x)=是奇函数,则x>0时,g(x)的解析式为( ) A.g(x)=- B.g(x)= C.g(x)=-2x D.g(x)=2x 命题角度2 奇偶性与单调性 【例3】 (1)设偶函数f(x)的定义域为R,当x∈[0,+∞)时,f(x)是增函数,则f(-),f(π),f(-3)的大小关系是( ) A.f(π)>f(-3)>f(-) B.f(π)>f(-)>f(-3) C.f(π)0时,f(x)=log2x-1, 则f(-)=( ) A. B.- C. D.- (2)设函数f(x)=log2|x|-x-2,则不等式f(x-2)≥f(2x+2)的解集为( ) A.[-4,0] B.[-4,0) C.[-4,-1)∪(-1,0] D.[-4,-1)∪(-1,0) 考点3 函数的周期性及应用 【例4】 (1)若 x∈R,f(x)+f(x+3)=1-f(x)f(x+3),f(-1)=0,则f(2 024)的值为( ) A.2 B.1 C.0 D.-1 (2)设f(x)是定义在R上以2为周期的奇函数,当x∈[0,1)时,f(x)=log2(x+1),则函数f(x)在[4,6]上的解析式是____________. 【对点训练3】 (1)定义在R上的奇函数f(x),满足f(x+3)=f(1-x),x∈[0,2]时,f(x)=mex-1,则f(31)=( ) A.e+1 B.e-1 C.1-e D.-e 若定义在R上的函数f(x),满足2f(x+y)f(x-y)=f(2x)+f(2y),且f(1)=-1,则f(0)+f(1)+f(2)+…+f(2 024)=( )A.0 B.-1 C.2 D.1 二次备课
板书设计
作业设计
教学反思
课 题 2.3 函数的奇偶性、周期性
教学目标 1.了解函数的奇偶性、周期性的概念和几何意义. 2.掌握函数的奇偶性、周期性的简单应用.
教学重点 了解函数的奇偶性、周期性的概念和几何意义
教学难点 掌握函数的奇偶性、周期性的简单应用
教法与学法指导 讲授法、合作探究法
教学准备 导学案提前预习;多媒体课件
教学过程
【高考链接】 1. 5年真题考点分布 5年考情考题示例考点分析2025年全国Ⅱ卷由奇偶性求函数解析式,函数奇偶性的应用2025年全国I卷利用函数奇偶性和周期性求函数值2023全国Ⅱ卷已知函数的奇偶性求参数2023年全国甲卷(理)已知函数的奇偶性求参数2022年全国乙卷(理)函数的奇偶性、单调性、对称性和周期性 (抽象函数)2022年全国I卷函数的对称性和周期性求函数值2021年全国I卷已知函数的奇偶性求参2021年全国Ⅱ卷函数的奇偶性、对称性和周期性2021年全国甲卷(理)由函数的奇偶性、周期性求函数值2021年全国乙卷(理)判断函数的奇偶性
命题规律及备考策略 本节是高考的一个重点,函数的单调性、奇偶性、对称性、周期性是高考的必考内容,重点关注周期性、奇偶性、对称性结合在一起,与函数图像、函数零点和不等式相结合进行考查。 该内容是新高考卷的必考内容,一般会以抽象函数作为载体,考查函数的单调性、奇偶性、周期性及对称性,是新高考一轮复习的重点内容. 高考链接 1.(2024·天津·高考真题)下列函数是偶函数的是( ) A. B. C. D. 2.(2024·上海·高考真题)已知,,且是奇函数,则 . 3.(2023·全国甲卷·高考真题)若为偶函数,则 . 4.(2023·全国乙卷·高考真题)已知是偶函数,则( ) A. B. C.1 D.2 5.(2023·全国新Ⅱ卷·高考真题)若为偶函数,则( ). A. B.0 C. D.1 6.(2022·全国乙卷·高考真题)若是奇函数,则 , . 7.(2021·全国甲卷·高考真题)设是定义域为R的奇函数,且.若,则( )A. B. C. D. 4.导入新课 1.函数的奇偶性 奇偶性定义图象特点偶函数一般地,设函数f(x)的定义域为D,如果 x∈D,都有-x∈D,且f(-x)=f(x),那么函数f(x)就叫做偶函数关于y轴对称奇函数一般地,设函数f(x)的定义域为D,如果 x∈D,都有-x∈D,且f(-x)=-f(x),那么函数f(x)就叫做奇函数关于原点对称
2.函数的周期性 (1)周期函数:一般地,设函数f(x)的定义域为D,如果存在一个非零常数T,使得对每一个x∈D都有x+T∈D,且f(x+T)=f(x),那么函数y=f(x)就叫做周期函数,非零常数T叫做这个函数的周期. (2)最小正周期:如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期. 重点结论 1.奇函数在关于原点对称的区间上具有相同的单调性;偶函数在关于原点对称的区间上具有相反的单调性. 2.函数周期性常用结论 对f(x)定义域内任意自变量的值x: (1)若f(x+a)=-f(x),则T=2a(a>0). (2)若f(x+a)=,则T=2a(a>0). 3.判断函数奇偶性的方法 (1)定义法 (2)图象法 (3)性质法 在公共定义域内有:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇. 注意:函数定义域关于原点对称是函数具有奇偶性的前提条件. 4.函数奇偶性的应用 (1)求函数值或参数的取值,求解的关键在于借助奇偶性转化为求已知区间上的函数值,或得到关于参数的恒等式,利用方程思想求参数的值. (2)比较大小,利用奇偶性把不在同一单调区间上的两个或多个自变量的函数值转化到同一单调区间上,进而利用其单调性比较大小. (3)解抽象函数不等式,先把不等式转化为f(g(x))>f(h(x))的形式,利用单调性把符号“f”脱掉,得到具体的不等式(组). 考点1 函数奇偶性的判断 【例1】 判断下列函数的奇偶性: (1)f(x)=+;(2)f(x)=(3)f(x)=log2(x+). 【对点训练1】 (1)(2024·天津卷)下列函数是偶函数的是( ) A.f(x)= B.f(x)= C.f(x)= D.f(x)= (2)已知f(x)为R上的奇函数,g(x)为R上的偶函数,且g(x)≠0,则下列说法正确的是( ) A.f(x)+g(x)为R上的奇函数 B.f(x)-g(x)为R上的偶函数 C.为R上的偶函数 D.|f(x)g(x)|为R上的偶函数 考点2 函数奇偶性的应用 命题角度1 利用函数的奇偶性求值(解析式) 【例2】 (1)若函数f(x)=是奇函数,则实数a=( ) A.0 B.-1 C.1 D.±1 (2)已知函数f(x)=是奇函数,则x>0时,g(x)的解析式为( ) A.g(x)=- B.g(x)= C.g(x)=-2x D.g(x)=2x 命题角度2 奇偶性与单调性 【例3】 (1)设偶函数f(x)的定义域为R,当x∈[0,+∞)时,f(x)是增函数,则f(-),f(π),f(-3)的大小关系是( ) A.f(π)>f(-3)>f(-) B.f(π)>f(-)>f(-3) C.f(π)
板书设计
作业设计
教学反思
同课章节目录
