六年级数学下册课件 反比例的意义 1(苏教版)
文档属性
| 名称 | 六年级数学下册课件 反比例的意义 1(苏教版) |  | |
| 格式 | rar | ||
| 文件大小 | 129.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-05 19:13:00 | ||
图片预览




文档简介
课件11张PPT。反比例的意义苏教版六年级数学下册教学目标1.理解反比例的意义。能够正确判断两种量是不是成反比例。
2.进一步认识事物之间的相互联系和发展变化规律。 3.初步渗透函数思想。
(1)表中有哪两种量?它们相关联吗?(2)观察表中的数据,这两种量的数值分别是怎样变化?(3)这种变化有没有规律?有什么规律?例:用60元去购买笔记本,笔记本的单价和数量如下表: 上表中,单价和数量是两种相关联的量,单价变化数量也随着变化的。数量扩大,单价反而缩小。
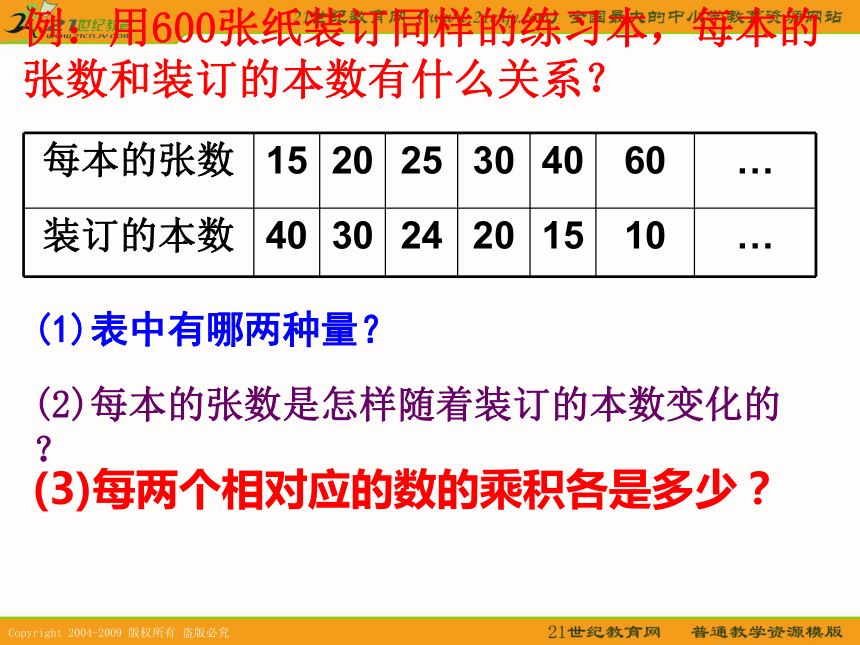
它们扩大、缩小的规律是:单价和数量的积总是一定的。例:用600张纸装订同样的练习本,每本的张数和装订的本数有什么关系?(1)表中有哪两种量?(2)每本的张数是怎样随着装订的本数变化的?(3)每两个相对应的数的乘积各是多少? 从上表看出,每本的张数和装订的本数也是两种相关联的量,装订本数是随着每本张数的变化而变化的。每本张数扩大,装订的本数反而缩小;每本的张数缩小,装订的本数反而扩大。它们扩大、缩小的规律是:
每本的张数和装订的本数的积总是一定的。 两种相关联的量,一种量变化,另一种量也随着变化。 如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量。它们的关系叫做反比例关系。 如果我们用字母x和y表示两种相关联的量,用k表示它们的积(一定),那么你能用字母将反比例关系表示出来吗?(一定)X×y=k1.判定两个量是否成反比例,主要看它们的( )是否一定。所以( )和( )是成反比例的量。 2.全班人数一定,每组的人数和组数。
( )和( )是相关联的量。每组的人数组数每组的人数×组数=全班人数(一定)每组的人数组数乘积帅莎步行从阁川到学校, 她每小时的速度与所用时间情况表:1.表中有哪两个有关联的量?每小时的速度、步行时间每小时的速度随着步行时间的扩大或缩小而同时缩小或扩大。3.相对应的速度与时间的乘积各是多少?2.每小时速度是怎样随着步行时间的变化而变化的?你能举出反比例的例子吗?这节课你学到了什么知识?
2.进一步认识事物之间的相互联系和发展变化规律。 3.初步渗透函数思想。
(1)表中有哪两种量?它们相关联吗?(2)观察表中的数据,这两种量的数值分别是怎样变化?(3)这种变化有没有规律?有什么规律?例:用60元去购买笔记本,笔记本的单价和数量如下表: 上表中,单价和数量是两种相关联的量,单价变化数量也随着变化的。数量扩大,单价反而缩小。
它们扩大、缩小的规律是:单价和数量的积总是一定的。例:用600张纸装订同样的练习本,每本的张数和装订的本数有什么关系?(1)表中有哪两种量?(2)每本的张数是怎样随着装订的本数变化的?(3)每两个相对应的数的乘积各是多少? 从上表看出,每本的张数和装订的本数也是两种相关联的量,装订本数是随着每本张数的变化而变化的。每本张数扩大,装订的本数反而缩小;每本的张数缩小,装订的本数反而扩大。它们扩大、缩小的规律是:
每本的张数和装订的本数的积总是一定的。 两种相关联的量,一种量变化,另一种量也随着变化。 如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量。它们的关系叫做反比例关系。 如果我们用字母x和y表示两种相关联的量,用k表示它们的积(一定),那么你能用字母将反比例关系表示出来吗?(一定)X×y=k1.判定两个量是否成反比例,主要看它们的( )是否一定。所以( )和( )是成反比例的量。 2.全班人数一定,每组的人数和组数。
( )和( )是相关联的量。每组的人数组数每组的人数×组数=全班人数(一定)每组的人数组数乘积帅莎步行从阁川到学校, 她每小时的速度与所用时间情况表:1.表中有哪两个有关联的量?每小时的速度、步行时间每小时的速度随着步行时间的扩大或缩小而同时缩小或扩大。3.相对应的速度与时间的乘积各是多少?2.每小时速度是怎样随着步行时间的变化而变化的?你能举出反比例的例子吗?这节课你学到了什么知识?
