1.3 第2课时 正方形的判定 课件(共38张PPT) 2025-2026学年北师大版九年级上册

(共38张PPT)
第一章 特殊平行四边形
1.3 正方形的性质与判定
第2课时 正方形的判定
第2课时 正方形的判定
情 境 导 入
两组对边分别平行
两组对边分别相等
一组对边平行且相等
两组对角分别相等
对角线互相平分
平行四边形
四边形
一组邻边相等
对角线互相垂直
菱形的判定
菱形
四边相等
两组对边分别平行
两组对边分别相等
一组对边平行且相等
两组对角分别相等
对角线互相平分
平行四边形
四边形
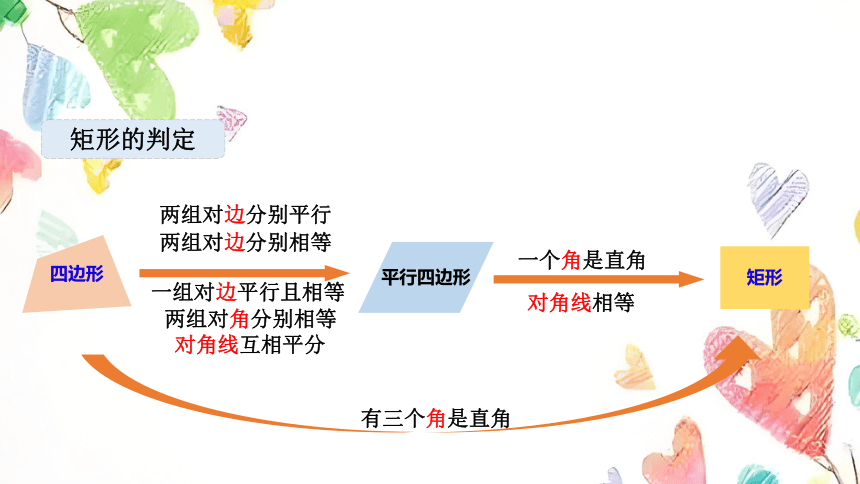
一个角是直角
对角线相等
矩形的判定
矩形
有三个角是直角
有一个角是直角
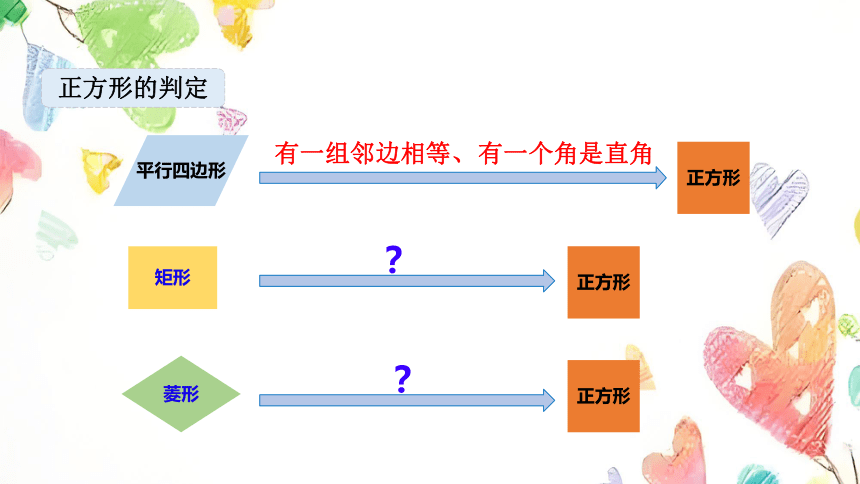
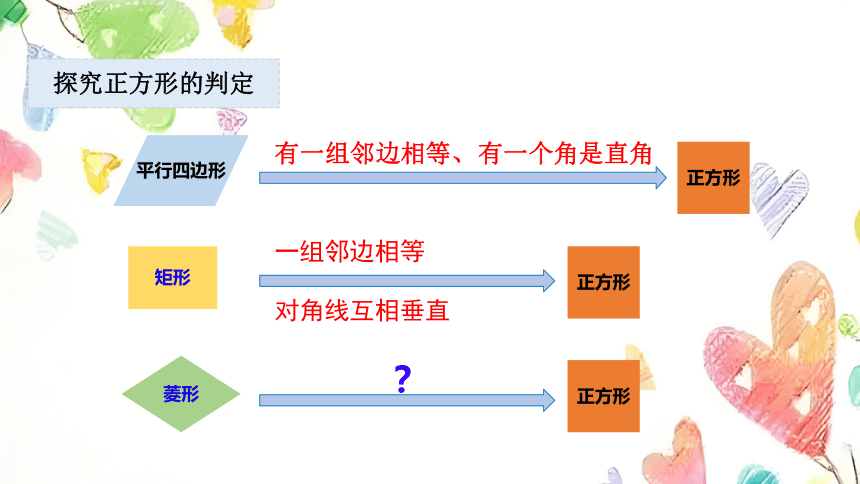
有一组邻边相等、
正方形
？
平行四边形
矩形
菱形
正方形
正方形
？
正方形的判定
探究正方形的判定
活动1：
如何将一张矩形纸片折叠剪出一个正方形？
满足怎样条件的矩形是正方形？
一组邻边
对角线
猜想
矩形
正方形
新 课 探 究
第2课时
正方形的判定
探究正方形的判定
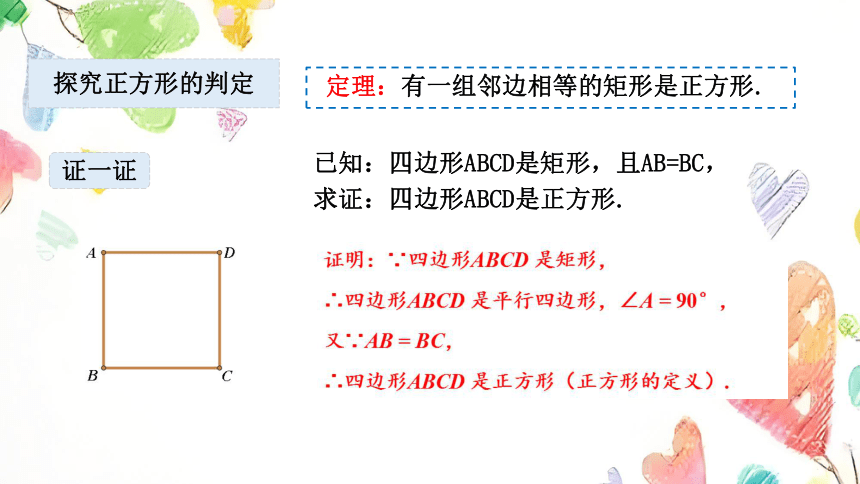
已知：四边形ABCD是矩形，且AB=BC，
求证：四边形ABCD是正方形.
证一证
定理：有一组邻边相等的矩形是正方形.
探究正方形的判定
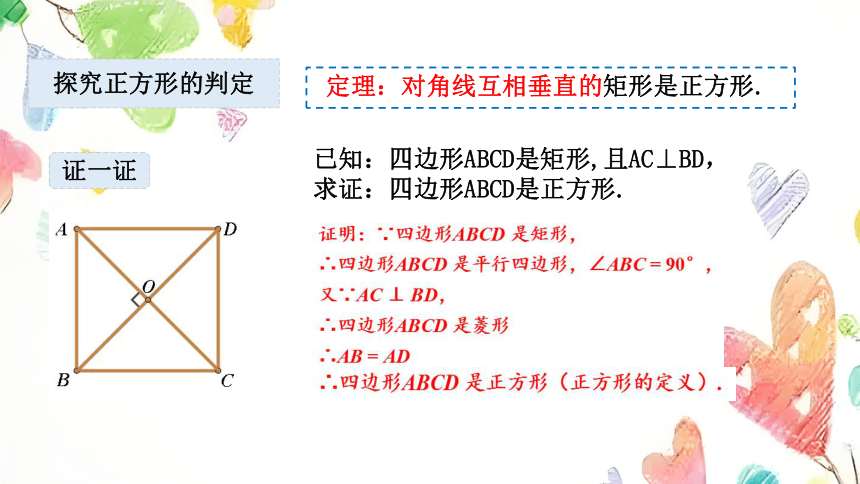
证一证
定理：对角线互相垂直的矩形是正方形.
已知：四边形ABCD是矩形,且AC⊥BD，
求证：四边形ABCD是正方形.
有一个角是直角
有一组邻边相等、
正方形
平行四边形
矩形
菱形
正方形
正方形
？
探究正方形的判定
一组邻边相等
对角线互相垂直
探究正方形的判定
证一证
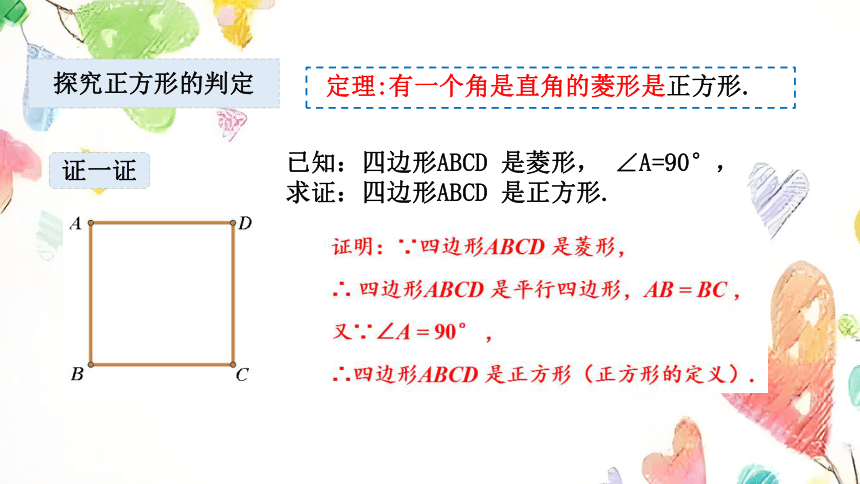
定理:有一个角是直角的菱形是正方形.
已知：四边形ABCD 是菱形， ∠A=90°，
求证：四边形ABCD 是正方形.
探究正方形的判定
证一证
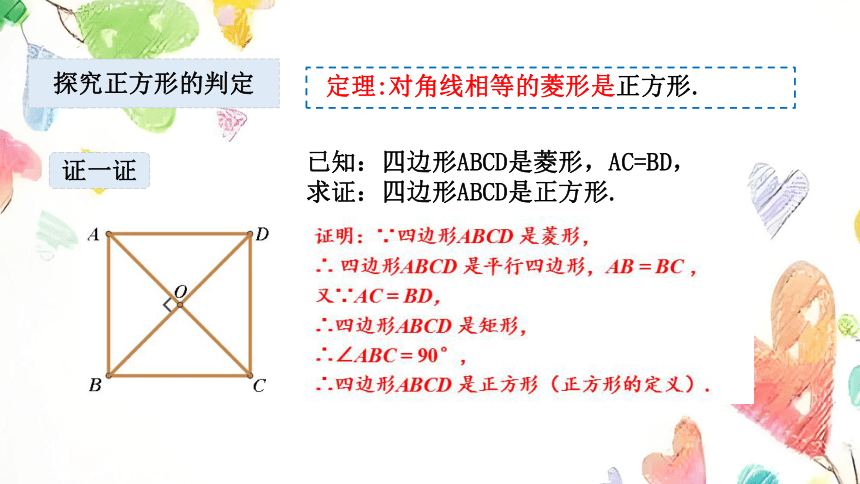
定理:对角线相等的菱形是正方形.
已知：四边形ABCD是菱形，AC=BD，
求证：四边形ABCD是正方形.
有一个角是直角
有一组邻边相等、
正方形
平行四边形
矩形
菱形
正方形
正方形
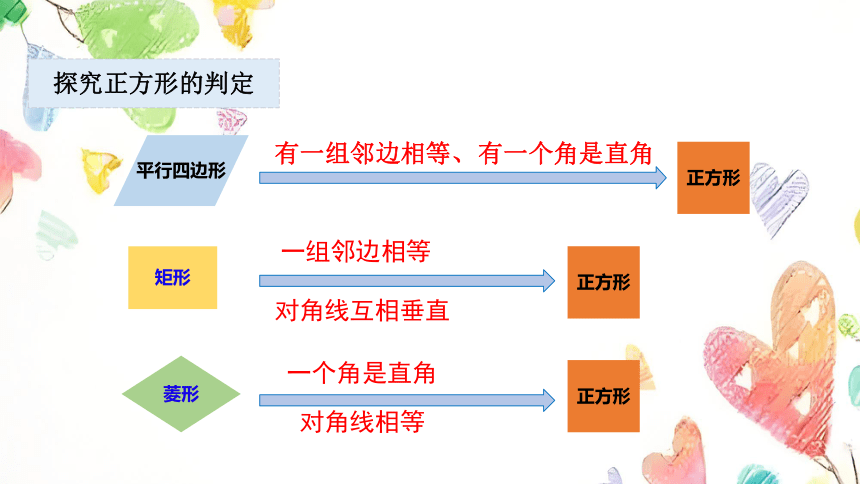
探究正方形的判定
一组邻边相等
对角线互相垂直
对角线相等
一个角是直角
探究正方形的判定
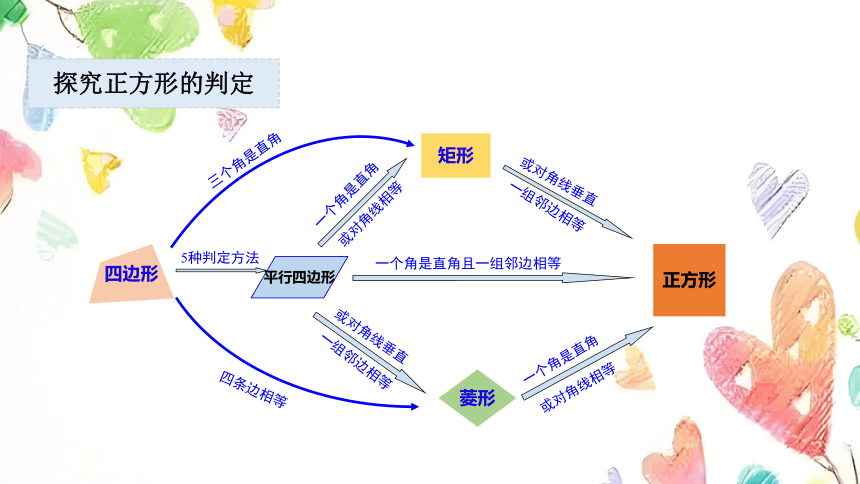
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形
矩形
菱形
正方形
四边形
已知：如图，在矩形ABCD中，BE 平分∠ABC，CE 平分∠DCB，
BF∥CE，CF∥BE，
求证：四边形BECF是正方形.
探究正方形的判定
证明：
探究四边形各边中点
顺次连接任意四边形各边中点所得的四边形是 .
任意画一个矩形、菱形、正方形，以四边的中点为顶点可以组成一个怎样的图形呢？先猜一猜，再证明。
任意四边形
平行四边形
顺次连接任意四边形各边中点所得的四边形是 .
任意画一个矩形、菱形、正方形，以四边的中点为顶点可以组成一个怎样的图形呢？先猜一猜，再证明。
菱形
矩形
探究四边形各边中点
顺次连接任意四边形各边中点所得的四边形是 .
任意画一个矩形、菱形、正方形，以四边的中点为顶点可以组成一个怎样的图形呢？先猜一猜，再证明。
菱形
矩形
探究四边形各边中点
顺次连接任意四边形各边中点所得的四边形是 .
任意画一个矩形、菱形、正方形，以四边的中点为顶点可以组成一个怎样的图形呢？先猜一猜，再证明。
正方形
正方形
探究四边形各边中点
以四边形各边中点为顶点所组成的新四边形的形状与哪些线段有关系？有怎样的关系？
新四边形的形状与原四边形两条对角线有关系.
新四边形的形状取决于原四边形两条对角线的位置关系和数量关系.
探究四边形各边中点
不垂直
不相等
不垂直
不相等
垂直
不相等
不垂直
相等
垂直
相等
平行四边形
平行四边形
矩形
菱形
正方形
探究四边形各边中点
1.对角线相等的四边形的中点四边形是 形。
2.对角线垂直的四边形的中点四边形是 形。
3.对角线相等且垂直的中点四边形是 形。
4.对角线既不相等也不垂直的中点四边形是 形。
菱
矩
正方
平行四边
探究四边形各边中点
巩固练习
1.下列命题正确的是（ ）
A.四个角都相等的四边形是正方形
B.四条边都相等的四边形是正方形
C.对角线相等的平行四边形是正方形
D.对角线互相垂直的矩形是正方形
D
巩固练习
2.如图，已知 ，其对角线的交点为，则下面说法正确的是( @13@ )
A
A. 当时，为矩形
B. 当时，为正方形
C. 当时，为菱形
D. 当时，为正方形
巩固练习
①②（答案不唯一）
3.小明在学习了正方形之后,给同桌小文出了一道题,从下列四个条件:① ,② ,③ ,④ 中选两个作为补充条件,使 为正方形（如图）,请填上一种你认为正确的选择：
巩固练习
4.如图,在 中,,平分 , ,.
求证:四边形 是正方形.
证明: ,
, ,
,
四边形 为矩形.
又 平分 , , ,
, 四边形 是正方形.
课 堂 小 结
1、这节课你都学会了什么？
2、将你的所学形成网络框架.
第2课时 正方形的判定
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形
矩形
菱形
正方形
四边形
1.如图，等边三角形AEF的顶点E，F在矩形ABCD的边BC，CD上，且∠CEF＝45°.求证：矩形ABCD是正方形.
证明：∵四边形ABCD是矩形，
∴∠B＝∠D＝∠C＝90°，
∵△AEF是等边三角形，
∴AE＝AF，∠AEF＝∠AFE＝60°，
∵∠CEF＝45°，∴∠CFE＝∠CEF＝45°，
∴∠AEB＝∠AFD＝180°－45°－60°＝75°，
∴△AEB≌△AFD(AAS)，∴AB＝AD，
∴矩形ABCD是正方形.
课后练习
2.(北师9上P25、人教8下P62)(2023梅州月考)如图，E，F，M，N分别是正方形ABCD四条边上的点，且AE＝BF＝CM＝DN.求证：四边形EFMN是正方形.

证明：∵AE＝BF＝CM＝DN，又∵AB＝BC＝CD＝AD，
∴AN＝BE＝CF＝DM.
∵∠A＝∠B＝∠C＝∠D＝90°，
∴△ANE≌△BEF≌△CFM≌△DMN.
∴EN＝EF＝MF＝NM，∠ENA＝∠DMN.
∴四边形EFMN是菱形.
∵∠ENA＝∠DMN，∠DMN＋∠DNM＝90°，
∴∠ENA＋∠DNM＝90°.∴∠ENM＝90°.
∴四边形EFMN是正方形.
小结：矩形+菱形→正方形.
3.已知在四边形ABCD中，AB＝BC＝CD＝AD，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是( )
A.AB∥CD B.∠A＝90°
C.AD∥BC　 D.∠A＝∠C
B
4.(2024佛山开学)从下列四个条件：①AB＝BC，②∠ABC＝90°，③AC＝BD，④AC⊥BD中选两个作为补充条件，使 ABCD成为正方形，你认为错误的是( )
A.①② B.①③ C.②③ D.③④
C
5. (北师9上P27)如图，在△ABC中，∠ABC＝90°，BD平分∠ABC，DE⊥BC，DF⊥AB.求证：四边形BEDF是正方形.
证明：∵∠ABC＝90°，DE⊥BC，DF⊥AB，
∴∠BFD＝∠BED＝∠ABC＝90°，
∴四边形BEDF是矩形.
又∵BD平分∠ABC，DE⊥BC，DF⊥AB，
∴DF＝DE，∴四边形BEDF是正方形.
小结：矩形+对角线垂直（或邻边相等）→正方形.
6.如图，AB是CD的垂直平分线，交CD于点M，过点M作ME⊥AC，MF⊥AD，垂足分别为E，F.

(1)求证：∠CAB＝∠DAB；
(2)若∠CAD＝90°，求证：四边形AEMF是正方形.
证明：(1)∵AB是CD的垂直平分线，∴AC＝AD，
又∵AB⊥CD，
∴∠CAB＝∠DAB(等腰三角形的三线合一).
(2)∵ME⊥AC，MF⊥AD，∠CAD＝90°，
即∠CAD＝∠AEM＝∠AFM＝90°，
∴四边形AEMF是矩形.
又∵∠CAB＝∠DAB，ME⊥AC，MF⊥AD，
∴ME＝MF，∴矩形AEMF是正方形.
解：四边形EFGH是正方形.证明如下：
由点E，F，G，H分别是正方形ABCD各边中点，
易得△AEH≌△BFE≌△CGF≌△DHG.
∴HE＝EF＝FG＝GH.∴四边形EFGH是菱形.
由题意可知△AEH和△BEF都是等腰直角三角形，
∴∠BEF＝∠AEH＝45°.
∴∠HEF＝90°.∴四边形EFGH是正方形.
7.(北师9上P23、人教8下P67)如图，顺次连接正方形ABCD的各边中点E，F，G，H，四边形EFGH是什么特殊四边形？先猜一猜，再证明.
小结：菱形+对角线相等（或有一个角为90°）→正方形.
★8. 0.50 (创新题)如图，在四边形ABCD中，AD∥BC，AD＝CD，E是对角线BD上一点，且EA＝EC.
(1)求证：四边形ABCD是菱形；
(2)如果BE＝BC，且∠CBE∶∠BCE＝2∶3，求证：四边形ABCD是正方形.
证明：(1)在△ADE和△CDE中， ，
∴△ADE≌△CDE，∴∠ADE＝∠CDE，
∵AD∥BC，∴∠ADE＝∠CBD，
∴∠CDE＝∠CBD，∴BC＝CD，
∵AD＝CD，∴BC＝AD，
又∵AD∥BC，∴四边形ABCD是平行四边形，
∵AD＝CD，∴四边形ABCD是菱形.
(2)∵BE＝BC，∴∠BCE＝∠BEC，
∵∠CBE∶∠BCE＝2 ∶3，
∴∠CBE＝180°＝45°，
∵四边形ABCD是菱形，∴∠ABE＝45°，
∴∠ABC＝90°，∴四边形ABCD是正方形.
THANK YOU