1.3正方形的性质与判定 同步练习(含答案)2025-2026学年北师大版九年级数学上册
文档属性
| 名称 | 1.3正方形的性质与判定 同步练习(含答案)2025-2026学年北师大版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 165.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-30 10:32:58 | ||
图片预览

文档简介
1.3正方形的性质与判定
一.选择题
1.正方形具有而矩形不一定具有的性质是( )
A.对角线相等
B.轴对称图形
C.对角线互相平分
D.对角线平分每一组对角
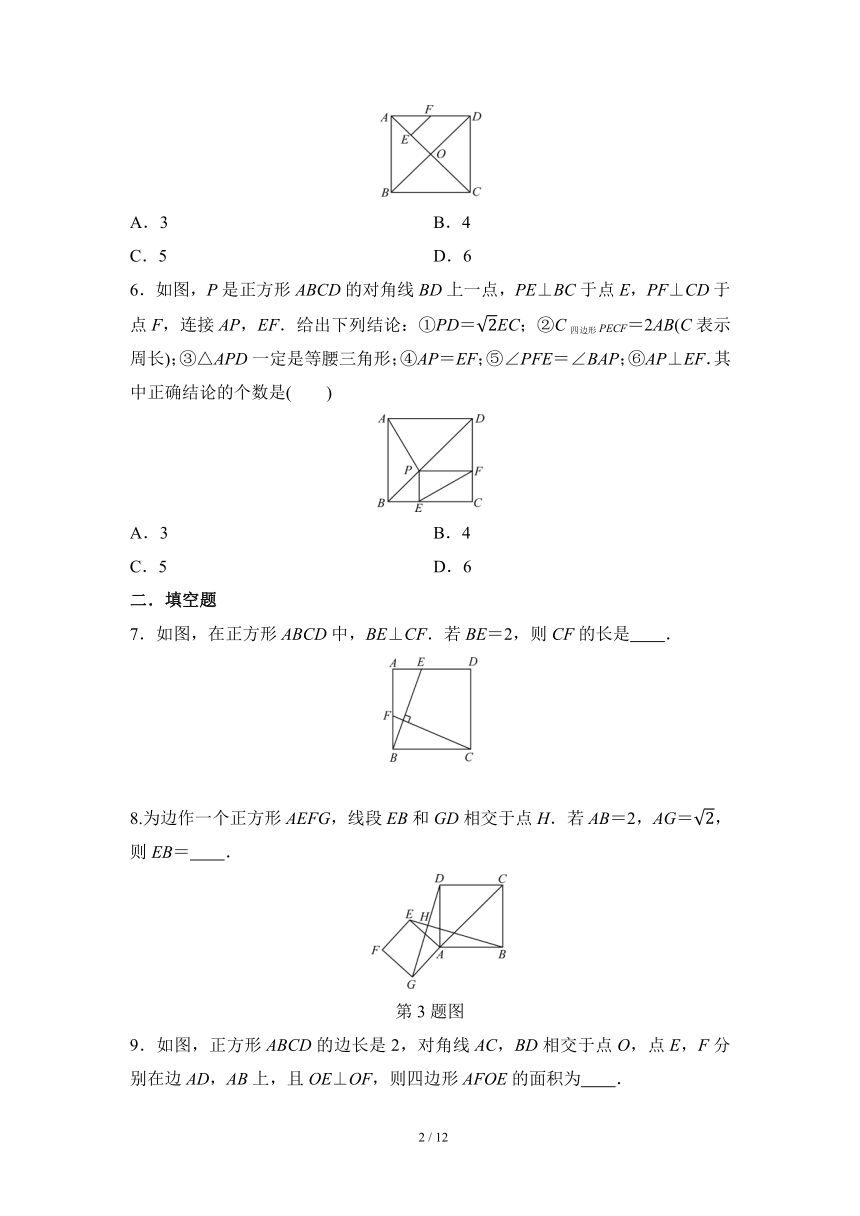
2.(2024·深圳龙岗区期中)如图,在正方形ABCD中,F为边AB上一点,CF与BD交于点E,连接AE.若∠BCF=25°,则∠AEF=( )
A.35° B.40°
C.45° D.50°
第2题图
3.如图,点G是正方形ABCD的对角线CA的延长线上任意一点,以线段AG 5.如图,在正方形OABC中,点A的坐标是(-3,1),则点C的坐标是( )
A.(1,3) B.(2,3)
C.(1,4) D.(3,1)
4.下列说法正确的是( )
A.对角线互相垂直的四边形是菱形
B.对角线互相垂直的四边形是矩形
C.对角线互相垂直的矩形是正方形
D.对角线互相垂直的菱形是正方形
5.如图,正方形ABCD的对角线AC,BD交于点O,E,F分别为AO,AD的中点.若EF=3,则OD的长是( )
A.3 B.4
C.5 D.6
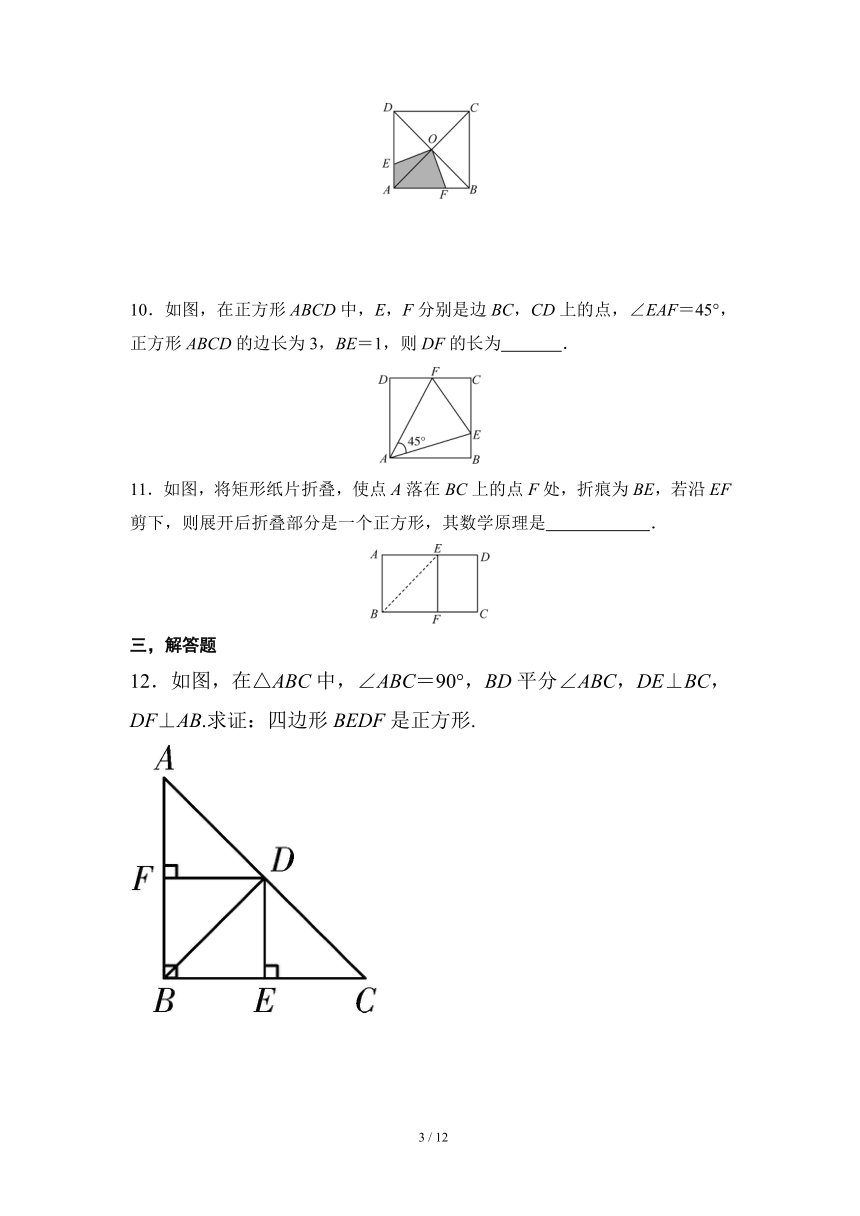
6.如图,P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②C四边形PECF=2AB(C表示周长);③△APD一定是等腰三角形;④AP=EF;⑤∠PFE=∠BAP;⑥AP⊥EF.其中正确结论的个数是( )
A.3 B.4
C.5 D.6
二.填空题
7.如图,在正方形ABCD中,BE⊥CF.若BE=2,则CF的长是 .
8.为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=2,AG=,则EB= .
第3题图
9.如图,正方形ABCD的边长是2,对角线AC,BD相交于点O,点E,F分别在边AD,AB上,且OE⊥OF,则四边形AFOE的面积为 .
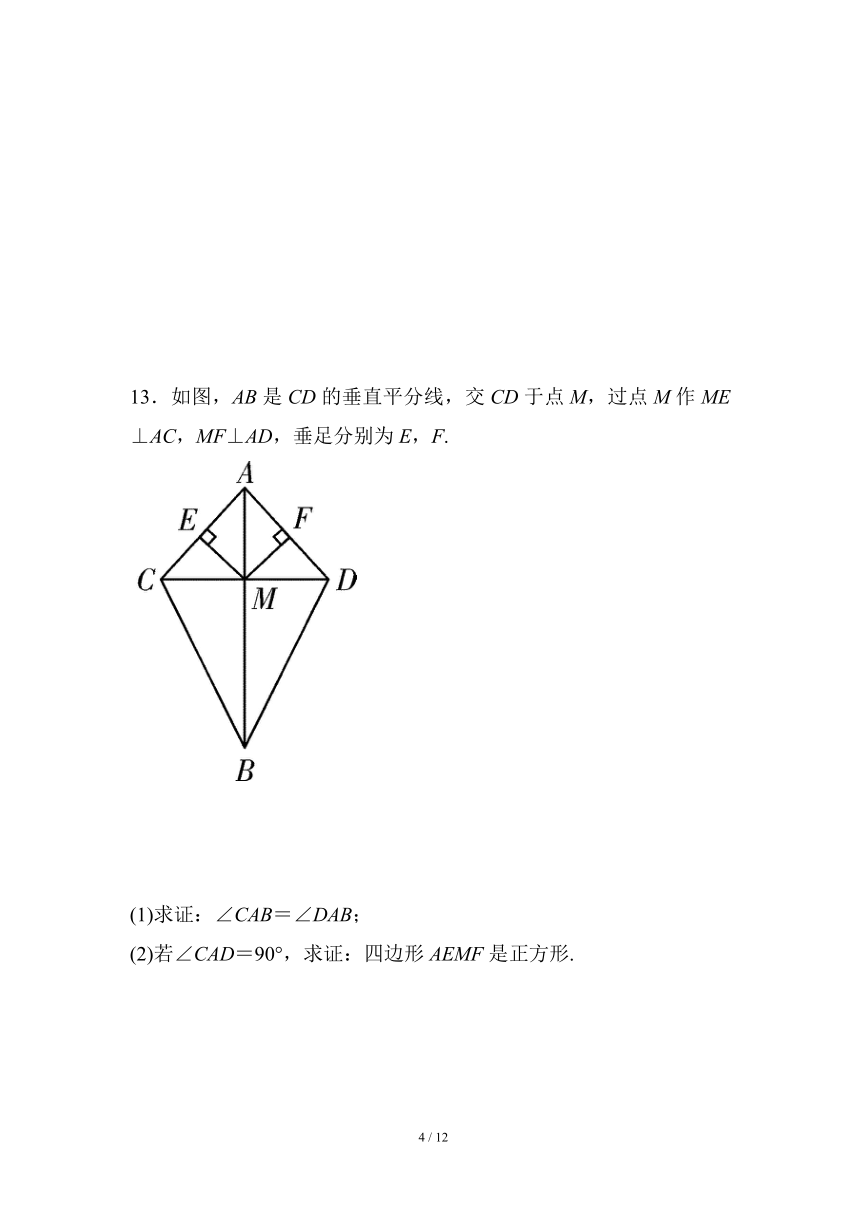
10.如图,在正方形ABCD中,E,F分别是边BC,CD上的点,∠EAF=45°,正方形ABCD的边长为3,BE=1,则DF的长为 .
11.如图,将矩形纸片折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则展开后折叠部分是一个正方形,其数学原理是 .
三,解答题
12.如图,在△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC,DF⊥AB.求证:四边形BEDF是正方形.
13.如图,AB是CD的垂直平分线,交CD于点M,过点M作ME⊥AC,MF⊥AD,垂足分别为E,F.
(1)求证:∠CAB=∠DAB;
(2)若∠CAD=90°,求证:四边形AEMF是正方形.
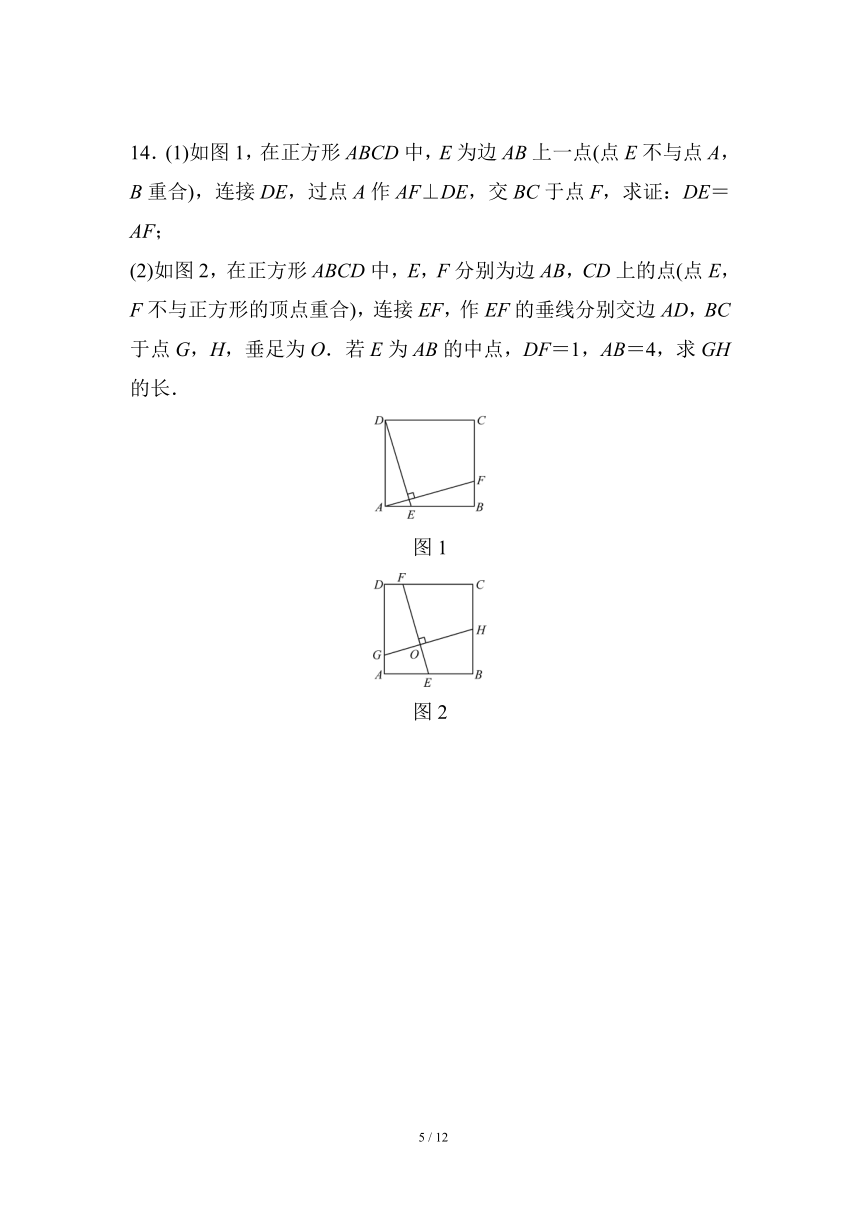
14.(1)如图1,在正方形ABCD中,E为边AB上一点(点E不与点A,B重合),连接DE,过点A作AF⊥DE,交BC于点F,求证:DE=AF;
(2)如图2,在正方形ABCD中,E,F分别为边AB,CD上的点(点E,F不与正方形的顶点重合),连接EF,作EF的垂线分别交边AD,BC于点G,H,垂足为O.若E为AB的中点,DF=1,AB=4,求GH的长.
图1
图2
1.3正方形的性质与判定
一.选择题
1.正方形具有而矩形不一定具有的性质是( D )
A.对角线相等
B.轴对称图形
C.对角线互相平分
D.对角线平分每一组对角
2.(2024·深圳龙岗区期中)如图,在正方形ABCD中,F为边AB上一点,CF与BD交于点E,连接AE.若∠BCF=25°,则∠AEF=( B )
A.35° B.40°
C.45° D.50°
第2题图
3.如图,点G是正方形ABCD的对角线CA的延长线上任意一点,以线段AG 5.如图,在正方形OABC中,点A的坐标是(-3,1),则点C的坐标是( A )
A.(1,3) B.(2,3)
C.(1,4) D.(3,1)
4.下列说法正确的是( C )
A.对角线互相垂直的四边形是菱形
B.对角线互相垂直的四边形是矩形
C.对角线互相垂直的矩形是正方形
D.对角线互相垂直的菱形是正方形
5.如图,正方形ABCD的对角线AC,BD交于点O,E,F分别为AO,AD的中点.若EF=3,则OD的长是( D )
A.3 B.4
C.5 D.6
6.如图,P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②C四边形PECF=2AB(C表示周长);③△APD一定是等腰三角形;④AP=EF;⑤∠PFE=∠BAP;⑥AP⊥EF.其中正确结论的个数是( C )
A.3 B.4
C.5 D.6
二.填空题
7.如图,在正方形ABCD中,BE⊥CF.若BE=2,则CF的长是 2 .
8.为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=2,AG=,则EB= .
第3题图
9.如图,正方形ABCD的边长是2,对角线AC,BD相交于点O,点E,F分别在边AD,AB上,且OE⊥OF,则四边形AFOE的面积为 1 .
10.如图,在正方形ABCD中,E,F分别是边BC,CD上的点,∠EAF=45°,正方形ABCD的边长为3,BE=1,则DF的长为 .
11.如图,将矩形纸片折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则展开后折叠部分是一个正方形,其数学原理是 邻边相等的矩形是正方形 .
三,解答题
12.如图,在△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC,DF⊥AB.求证:四边形BEDF是正方形.
证明:∵∠ABC=90°,DE⊥BC,DF⊥AB,
∴∠BFD=∠BED=∠ABC=90°,
∴四边形BEDF是矩形.
又∵BD平分∠ABC,DE⊥BC,DF⊥AB,
∴DF=DE,∴四边形BEDF是正方形.
13.如图,AB是CD的垂直平分线,交CD于点M,过点M作ME⊥AC,MF⊥AD,垂足分别为E,F.
(1)求证:∠CAB=∠DAB;
(2)若∠CAD=90°,求证:四边形AEMF是正方形.
证明:(1)∵AB是CD的垂直平分线,∴AC=AD,
又∵AB⊥CD,
∴∠CAB=∠DAB(等腰三角形的三线合一).
(2)∵ME⊥AC,MF⊥AD,∠CAD=90°,
即∠CAD=∠AEM=∠AFM=90°,
∴四边形AEMF是矩形.
又∵∠CAB=∠DAB,ME⊥AC,MF⊥AD,
∴ME=MF,∴矩形AEMF是正方形.
14.(1)如图1,在正方形ABCD中,E为边AB上一点(点E不与点A,B重合),连接DE,过点A作AF⊥DE,交BC于点F,求证:DE=AF;
(2)如图2,在正方形ABCD中,E,F分别为边AB,CD上的点(点E,F不与正方形的顶点重合),连接EF,作EF的垂线分别交边AD,BC于点G,H,垂足为O.若E为AB的中点,DF=1,AB=4,求GH的长.
图1
图2
(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠DAE=∠ABF=90°.
∴∠DAF+∠BAF=90°.
∵AF⊥DE,
∴∠DAF+∠ADE=90°.
∴∠ADE=∠BAF.
在△DAE和△ABF中,
∴△DAE≌△ABF(ASA).
∴DE=AF.
(2)解:如图,分别过点A,D作AN∥GH,DM∥EF,分别交BC,AB于点N,M.
∵四边形ABCD是正方形,
∴AB∥CD,AB=CD,∠DAB=∠B=90°.
∴四边形DMEF是平行四边形.
∴ME=DF=1,DM=EF.
∵DM∥EF,GH⊥EF,
∴DM⊥GH.
同理,四边形AGHN是平行四边形,
∴GH=AN.
∵AN∥GH,DM⊥GH,
∴AN⊥DM.
∴∠DAN+∠ADM=90°.
∵∠DAN+∠BAN=90°,
∴∠ADM=∠BAN.
在△ADM和△BAN中,
∴△ADM≌△BAN(ASA).
∴DM=AN.
∴DM=GH.
∵E为AB的中点,AB=4,
∴AE=AB=2.
∴AM=AE-ME=2-1=1.
在Rt△ADM中,AM=1,AD=4,
∴DM===.
∴GH=.
1 / 12
一.选择题
1.正方形具有而矩形不一定具有的性质是( )
A.对角线相等
B.轴对称图形
C.对角线互相平分
D.对角线平分每一组对角
2.(2024·深圳龙岗区期中)如图,在正方形ABCD中,F为边AB上一点,CF与BD交于点E,连接AE.若∠BCF=25°,则∠AEF=( )
A.35° B.40°
C.45° D.50°
第2题图
3.如图,点G是正方形ABCD的对角线CA的延长线上任意一点,以线段AG 5.如图,在正方形OABC中,点A的坐标是(-3,1),则点C的坐标是( )
A.(1,3) B.(2,3)
C.(1,4) D.(3,1)
4.下列说法正确的是( )
A.对角线互相垂直的四边形是菱形
B.对角线互相垂直的四边形是矩形
C.对角线互相垂直的矩形是正方形
D.对角线互相垂直的菱形是正方形
5.如图,正方形ABCD的对角线AC,BD交于点O,E,F分别为AO,AD的中点.若EF=3,则OD的长是( )
A.3 B.4
C.5 D.6
6.如图,P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②C四边形PECF=2AB(C表示周长);③△APD一定是等腰三角形;④AP=EF;⑤∠PFE=∠BAP;⑥AP⊥EF.其中正确结论的个数是( )
A.3 B.4
C.5 D.6
二.填空题
7.如图,在正方形ABCD中,BE⊥CF.若BE=2,则CF的长是 .
8.为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=2,AG=,则EB= .
第3题图
9.如图,正方形ABCD的边长是2,对角线AC,BD相交于点O,点E,F分别在边AD,AB上,且OE⊥OF,则四边形AFOE的面积为 .
10.如图,在正方形ABCD中,E,F分别是边BC,CD上的点,∠EAF=45°,正方形ABCD的边长为3,BE=1,则DF的长为 .
11.如图,将矩形纸片折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则展开后折叠部分是一个正方形,其数学原理是 .
三,解答题
12.如图,在△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC,DF⊥AB.求证:四边形BEDF是正方形.
13.如图,AB是CD的垂直平分线,交CD于点M,过点M作ME⊥AC,MF⊥AD,垂足分别为E,F.
(1)求证:∠CAB=∠DAB;
(2)若∠CAD=90°,求证:四边形AEMF是正方形.
14.(1)如图1,在正方形ABCD中,E为边AB上一点(点E不与点A,B重合),连接DE,过点A作AF⊥DE,交BC于点F,求证:DE=AF;
(2)如图2,在正方形ABCD中,E,F分别为边AB,CD上的点(点E,F不与正方形的顶点重合),连接EF,作EF的垂线分别交边AD,BC于点G,H,垂足为O.若E为AB的中点,DF=1,AB=4,求GH的长.
图1
图2
1.3正方形的性质与判定
一.选择题
1.正方形具有而矩形不一定具有的性质是( D )
A.对角线相等
B.轴对称图形
C.对角线互相平分
D.对角线平分每一组对角
2.(2024·深圳龙岗区期中)如图,在正方形ABCD中,F为边AB上一点,CF与BD交于点E,连接AE.若∠BCF=25°,则∠AEF=( B )
A.35° B.40°
C.45° D.50°
第2题图
3.如图,点G是正方形ABCD的对角线CA的延长线上任意一点,以线段AG 5.如图,在正方形OABC中,点A的坐标是(-3,1),则点C的坐标是( A )
A.(1,3) B.(2,3)
C.(1,4) D.(3,1)
4.下列说法正确的是( C )
A.对角线互相垂直的四边形是菱形
B.对角线互相垂直的四边形是矩形
C.对角线互相垂直的矩形是正方形
D.对角线互相垂直的菱形是正方形
5.如图,正方形ABCD的对角线AC,BD交于点O,E,F分别为AO,AD的中点.若EF=3,则OD的长是( D )
A.3 B.4
C.5 D.6
6.如图,P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD=EC;②C四边形PECF=2AB(C表示周长);③△APD一定是等腰三角形;④AP=EF;⑤∠PFE=∠BAP;⑥AP⊥EF.其中正确结论的个数是( C )
A.3 B.4
C.5 D.6
二.填空题
7.如图,在正方形ABCD中,BE⊥CF.若BE=2,则CF的长是 2 .
8.为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=2,AG=,则EB= .
第3题图
9.如图,正方形ABCD的边长是2,对角线AC,BD相交于点O,点E,F分别在边AD,AB上,且OE⊥OF,则四边形AFOE的面积为 1 .
10.如图,在正方形ABCD中,E,F分别是边BC,CD上的点,∠EAF=45°,正方形ABCD的边长为3,BE=1,则DF的长为 .
11.如图,将矩形纸片折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则展开后折叠部分是一个正方形,其数学原理是 邻边相等的矩形是正方形 .
三,解答题
12.如图,在△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC,DF⊥AB.求证:四边形BEDF是正方形.
证明:∵∠ABC=90°,DE⊥BC,DF⊥AB,
∴∠BFD=∠BED=∠ABC=90°,
∴四边形BEDF是矩形.
又∵BD平分∠ABC,DE⊥BC,DF⊥AB,
∴DF=DE,∴四边形BEDF是正方形.
13.如图,AB是CD的垂直平分线,交CD于点M,过点M作ME⊥AC,MF⊥AD,垂足分别为E,F.
(1)求证:∠CAB=∠DAB;
(2)若∠CAD=90°,求证:四边形AEMF是正方形.
证明:(1)∵AB是CD的垂直平分线,∴AC=AD,
又∵AB⊥CD,
∴∠CAB=∠DAB(等腰三角形的三线合一).
(2)∵ME⊥AC,MF⊥AD,∠CAD=90°,
即∠CAD=∠AEM=∠AFM=90°,
∴四边形AEMF是矩形.
又∵∠CAB=∠DAB,ME⊥AC,MF⊥AD,
∴ME=MF,∴矩形AEMF是正方形.
14.(1)如图1,在正方形ABCD中,E为边AB上一点(点E不与点A,B重合),连接DE,过点A作AF⊥DE,交BC于点F,求证:DE=AF;
(2)如图2,在正方形ABCD中,E,F分别为边AB,CD上的点(点E,F不与正方形的顶点重合),连接EF,作EF的垂线分别交边AD,BC于点G,H,垂足为O.若E为AB的中点,DF=1,AB=4,求GH的长.
图1
图2
(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠DAE=∠ABF=90°.
∴∠DAF+∠BAF=90°.
∵AF⊥DE,
∴∠DAF+∠ADE=90°.
∴∠ADE=∠BAF.
在△DAE和△ABF中,
∴△DAE≌△ABF(ASA).
∴DE=AF.
(2)解:如图,分别过点A,D作AN∥GH,DM∥EF,分别交BC,AB于点N,M.
∵四边形ABCD是正方形,
∴AB∥CD,AB=CD,∠DAB=∠B=90°.
∴四边形DMEF是平行四边形.
∴ME=DF=1,DM=EF.
∵DM∥EF,GH⊥EF,
∴DM⊥GH.
同理,四边形AGHN是平行四边形,
∴GH=AN.
∵AN∥GH,DM⊥GH,
∴AN⊥DM.
∴∠DAN+∠ADM=90°.
∵∠DAN+∠BAN=90°,
∴∠ADM=∠BAN.
在△ADM和△BAN中,
∴△ADM≌△BAN(ASA).
∴DM=AN.
∴DM=GH.
∵E为AB的中点,AB=4,
∴AE=AB=2.
∴AM=AE-ME=2-1=1.
在Rt△ADM中,AM=1,AD=4,
∴DM===.
∴GH=.
1 / 12
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
