贵州省黔南州2024-2025学年高一下学期期末考试数学试卷(含解析)
文档属性
| 名称 | 贵州省黔南州2024-2025学年高一下学期期末考试数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 00:00:00 | ||
图片预览




文档简介
贵州省黔南州 2024-2025 学年高一下学期期末质量监测
数学试卷
一、单选题
已知集合M x 1 x 4 , N x x 2 0 ,则 M ∩ N ( )
( 1, 4]
( 1, 4)
(2, 4) D. (2, 4]
样本数据 2,3,6,8,9,10 的中位数是( )
A.6 B.7 C.8 D.9
在V ABC 中,E 为边 BC 上的一点,且 BE 3EC ,则 AE ( )
1 –––→
AB
3 –––→
AC
3 –––→
AB
1 –––→
AC
4 4 4 4
3 –––→
AB
5 –––→
AC
1 –––→
AB
2 –––→
AC
8 8 3 3
从 0~9 这 10 个数中随机选择一个数,则事件“这个数平方的个位上的数字是 6”的概率为( )
A. 1
10
B. 1
5
C. 3
10
D. 2
5
已知圆台上底面半径为 1,下底面半径为 2,母线长为 2,则圆台的体积为( )
3 3π B. 8 3π
3
7 3π
3
2 3π
某校在校园科技节期间举办了“智能机器人挑战 ”,为了解高一年级 500 名学生观看比的情况,该校学生会用随机抽样的方式抽取了一个容量为 50 的样本进行调查,并将数据整理后,列表如下:
从表中可以得出正确的结论为( )
估计观看比场数的极差为 6 B.估计观看比场数的众数为 2
C.估计观看比不低于 4 场的学生约为 200 人 D.估计观看比不超过 2 场的学生概率为0.4
如图,某数学建模活动小组为了测量河对岸的塔高 AB ,选取与塔底 B 在同一平面的两个测量基点 C 与 D.现测量得 BCD 30 , BDC 120 , CD 10m ,在点 C 处测得塔顶 A 的仰角为 60°,则塔高 AB ( )
0m B. 20 3m C.30m D. 30 3m
函数 f (x) [x] 的函数值表示不超过 x 的最大整数,例如,[ 3.5] 4,[2.1] 2 ,则函数 g(x) x [x] 的
值域为( )
[0,1) B. (0,1] C. ( 1, 0)
D. ( 1,1]
二、多选题
已知复数 z 1 2i (i 是虚数单位),则下列说法正确的是( )
| z | B.z 的虚部是 2
复数 z 的共轭复数为z 1 2i
复数 z 在复平面内对应的点位于第四象限
已知事件 A,B 满足 P( A) 0.1, P(B) 0.6 ,则下列说法正确的是( )
事件 A 与事件 B 可能为对立事件
若事件 A 与事件 B 相互独立,则它们的对立事件也相互独立
若事件 A 与事件 B 互斥,则 P( A B) 0.7
若事件 A 与事件 B 相互独立,则 P( AB) 0.06
如图,在棱长为 2 的正方体 ABCD A1B1C1D1 中,M,N,P 分别是 BB1 , DD1, C1D1 的中点,Q 是侧面 BCC1B1
内的动点(含边界),则下列结论正确的是( )
A, B1 , P, N 四点共面
异面直线CD 与 BC 所成的角为 π
1 1 4
当点 Q 在线段 B1C 上运动时,三棱锥 A1 BDQ 的体积为定值
当 NQ 2
时,点 Q 的运动轨迹的长度为 2π
3
三、填空题
2
已知θ为锐角,且cosθ ,则tanθ .
3
在一次猜灯谜活动中,共有 10 道灯谜、甲、乙两名同学独立竞猜,甲同学猜对了 8 道,乙同学猜对了
4 道,假设猜对每道灯谜是等可能的.若任选一道灯谜,则恰有一人猜对的概率为 .
在《九章算术》中,底面是直角三角形的直三棱柱被称为“堑堵”.如图,三棱柱 ABC A1B1C1 为一“堑堵”,P 是 BB1 的中点, AA1 AC BC 4 ,则该“堑堵”的外接球的表面积为 ;在过点 P 且与直线 AC1
平行的截面中,当截面图形为等腰梯形时,该截面的面积为
四、解答题
已知函数 f (x) lg(1 x) lg(1 x) .
求函数 f (x) 的定义域 M;
判断函数 f (x) 的奇偶性,若 f (t) 2 ,求 f ( t) 的值.
已知平面向量 → (1, 2), b → (2, y) ,且 → → → .
求b 和c 的坐标;
求向量2a 与向量b → 的夹角的余弦值.
在V ABC 中, c ,再从下面两个条件中,选出一个作为已知条件,解答下面的问题.条件①:
c sin A 3a cos C ;条件②: (a b)2 c2 ab .
若b 2 ,求V ABC 的面积;
求a b 的取值范围.
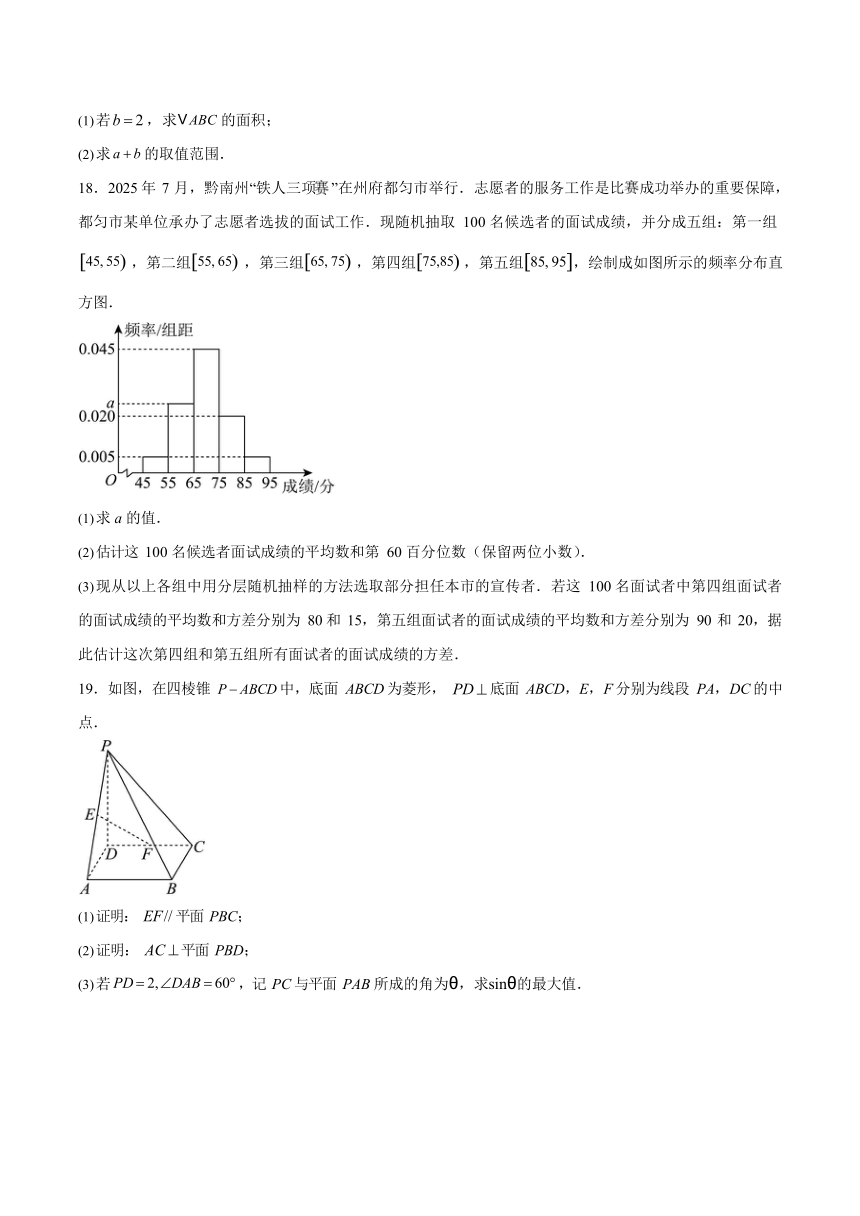
18.2025 年 7 月,黔南州“铁人三项 ”在州府都匀市举行.志愿者的服务工作是比成功举办的重要保障,都匀市某单位承办了志愿者选拔的面试工作.现随机抽取 100 名候选者的面试成绩,并分成五组:第一组
45, 55 ,第二组 55, 65 ,第三组 65, 75 ,第四组 75,85 ,第五组 85, 95 ,绘制成如图所示的频率分布直方图.
求 a 的值.
估计这 100 名候选者面试成绩的平均数和第 60 百分位数(保留两位小数).
现从以上各组中用分层随机抽样的方法选取部分担任本市的宣传者.若这 100 名面试者中第四组面试者的面试成绩的平均数和方差分别为 80 和 15,第五组面试者的面试成绩的平均数和方差分别为 90 和 20,据此估计这次第四组和第五组所有面试者的面试成绩的方差.
19.如图,在四棱锥 P ABCD 中,底面 ABCD 为菱形, PD 底面 ABCD,E,F 分别为线段 PA,DC 的中点.
证明: EF // 平面 PBC;
证明: AC 平面 PBD;
若 PD 2, DAB 60 ,记 PC 与平面 PAB 所成的角为θ,求sinθ的最大值.
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A B C D C A AB BCD
题号 11
答案 ACD
1.D
根据集合的交集运算求解.
【详解】M ∩ N {x∣ 1 x 4}∩{x∣x 2 0} {x∣ 1 x 4}∩{x∣x 2} {x∣2 x 4} (2, 4] .故选:D.
2.B
根据中位数的定义求解.
【详解】因为样本数据个数是偶数,所以这组数据的中位数是第 3 位数和第 4 位数的平均数,
即 6 8 7 .
2
故选:B.
3.A
利用向量的线性运算,结合线段的比例关系来推导 AE 的表达式.
–––→ –––→ –––→ –––→
【详解】由图形可知: AE AB BE AB
3 –––→
BC
1 –––→
AB
3 –––→
AC .
故选:A 4.B
利用列举法求解出古典概型的概率.
4 4 4
【详解】从 0~9 这 10 个数中随机选择一个数,共有 10 种可能,其样本空间可表示为
{0,1, 2, 3, 4, 5, 6, 7,8, 9},
若一个数平方的个位上的数字是 6,则该数是 4 或 6,共 2 种情况,故所求概率为 2 1 .故 B 正确.
10 5
故选:B.
5.C
利用圆台体积公式即可求得结果.
【详解】设上、下底面的半径分别为r1 , r2 ,高为 h,母线l 2 ,
则S πr 2 π, S
πr 2 4π , h
3 ,
1 1 2 2
所以V 1 S
S
h 1 π
π 4π 4π 7 3π .
3
故选:C.
1
2 3 3
6.D
A 选项,利用极差的定义得到答案;B 选项,先求出m 16 ,比较频率得到众数为 1;C 选项,求出观看比 不低于 4 场的学生所占百分比,进而求出学生约为 220 人;D 选项,计算出观看比不超过 2 场的学生频率,进而判断 D 选项.
【详解】A 选项,由表可知,估计观看比场数的极差为7 0 7 ,A 错误; B 选项,由频率分布表的性质,得m 100 7 18 15 10 14 15 5 16 . 由表知,出现频率最高的场数为 1,所以众数为 1,B 错误;
C 选项,因为观看比不低于 4 场的学生所占百分比为10% 14% 15% 5% 44% ,所以估计观看比不低于 4 场的学生约为500 44% 220 (人),C 错误;
D 选项,估计观看比不超过 2 场的学生概率为7% 18% 15% 40% 0.4 ,D 正确.故选:D.
7.C
在△BCD 中,由正弦定理求得 BC 10 3 ,在Rt△ABC 中,解直角三角形得解.
【详解】在△BCD 中,由三角形内角和定理,
得 CBD 180 BDC BCD 180 120 30 30 .
由正弦定理,得
BC
sin BDC
CD
sin CBD
,即 BC
sin120
10
sin 30
,解得 BC 10 3 .
在Rt△ABC 中, AB BC tan 60 10 3 30 ,即塔高 AB 30m .故选:C.
8.A
根据取整函数的定义求函数的值域.
【详解】设 x a b ,其中a x , b 为 x 的小数部分,则0 b 1 ,则 g(x) x [x] b 0,1 ,
所以函数 g(x) 的值域为: 0,1 .
故选:A
AB
对 A,利用复数模公式求解;对 B,根据复数虚部概念判断;对 C,根据共轭复数的定义判断;对 D,根据复数的几何意义判断.
【详解】对于 A, | z | 5 ,故 A 正确;
对于 B,复数 z 1 2i 的虚部为 2,故 B 正确;
对于 C,复数 z 1 2i 的共轭复数为 z 1 2i ,故 C 错误;
对于 D,因为复数 z 在复平面内对应的点的坐标为( 1, 2) ,则复数 z 在复平面内对应的点位于第二象限,故
D 错误.
故选:AB.
BCD
利用事件的对立可对 A 判断;由利用相互独立事件的定义,可对 B 判断;利用互斥事件的概率公式,即可对 C 判断;利用相互独立事件的概率公式即可对 D 判断.
【详解】对于 A,由对立事件的概率和为 1,但 P( A) P(B) 0.7 1,故 A 错误;
对于 B,根据相互独立事件的性质可得事件A 与事件 B 相互独立,则它们的对立事件也相互独立,故 B 正确;
对于 C,若事件A 与事件 B 互斥,则 P( A B) P( A) P(B) 0.7 ,故 C 正确;
对于 D,根据相互独立事件的定义, P( AB) P( A)P(B) 0.06 ,故 D 正确.故选:BCD.
ACD
对 A,由题可得 AB1 / / DC1 ,PN / / DC1 ,得 AB1 / / PN 得证;对 B,连接 AD1 , CD1 , AC, BC1 ,可得异面直线CD1
与 BC1 所成的角为 AD1C ,求解判断;对 C,由等体积法,可得VA BDQ VQ A BD ,求解判断;对 D,由题可得点 Q 的运动轨迹是在侧面 BCC1B1 内以CC1 的中点为圆心,半径r 2 的圆弧 H MG ,求解判断.
【详解】对于 A,如图 1,在正方体中,易知 AB1 / / DC1 .
又 P,N 分别是C1D1 , DD1 的中点,则 PN / / DC1 ,所以 AB1 / / PN ,即 A, B1 , P, N 四点共面,故 A 正确;对于 B,如图 2,分别连接 AD1 , CD1 , AC, BC1 ,由题意,易知 BC1 / / AD1 ,
则异面直线CD 与 BC 所成的角为 AD C ,易知VAD C 为等边三角形,故 AD C π ,故 B 错误;
1 1 1 1 1 3
对于 C,如图 3,由等体积法,得VA BDQ VQ A BD .
因为 B1C / / A1D ,可得 B1C / / 平面 A1BD ,又点 Q 在线段 B1C 上运动,所以点 Q 到平面 A1BD 的距离为定值.又S△A BD 也为定值,
所以VQ A BD 为定值,即VA BDQ VQ A BD 为定值,
1 1 1
且V V V V
1 S
AA 1 1 2 2 2 4 ,故 C 正确;
A1 BDQ Q A1BD C A1BD A1 BCD
3 △BCD
1 3 2 3
对于 D,如图 4,取CC1 的中点O ,易得ON 平面 BCC1B1 ,
当 NQ 2
时,点 Q 的运动轨迹是在侧面 BCC1B1 内以CC1 的中点O 为圆心,半径r 2 的圆弧 H MG ,
在RtVOC H 中,由OH 2 , C O 1 ,可得 C OH π ,同理, GOC π ,
1 1 1 3 3
所以圆弧 H MG 圆心角为α π ,所以点 Q 的运动轨迹的长度为l αr π 2 2π ,故 D 正确.
3 3 3
故选:ACD.
12. 5
2
根据sin2θ cos2θ 1,且θ为锐角,推出sinθ
sinθ
1 cos2 θ,根据tanθ 即可求解.
cos
【详解】因为θ为锐角,且cosθ 2 ,所以sinθ
3
1 cos2θ
5 ,
3
故tanθ sinθ
cosθ
5
3 5 .
2 2
3
故答案为: 5 .
2
14 /0.56
25
已知甲、乙两人猜灯谜的独立事件恰有一人猜对的概率 P, 设事件 A 表示“甲猜对”,事件 B 表示“乙猜对”,则
P P( AB ∪ AB) P( A)P(B) P( A)P(B) .
【详解】设事件 A 表示“甲猜对”,事件 B 表示“乙猜对”,则 P( A) 8 4 , P(B) 4 2 ,
所以任选一道灯谜,恰有一个人猜对的概率为:
10 5
10 5
P( AB AB) P( A)P(B) P( A)P(B) 4 1 2 1 4 2 14 .
5 5 5 5 25
故答案为: 14 .
25
48π 6
①如图 1,把原三棱柱补成正方体,则正方体对角线为外接球的一条直径,根据2R 求
出半径,再根据面积公式S 4πR2 求解.
②如图 2,取中点 E,F,G 构造面 FGPE ,由 EF 与 AC1 线线平行推出 AC1 与面 FGPE 平行,根据边长关系进一步推出四边形 FGPE 即为唯一的等腰梯形,求其面积即可.
【详解】如图 1,将三棱柱 ABC A1B1C1 补成正方体 ACBQ A1C1B1Q1 ,
则外接球的半径 R 2 3 ,则外接球的表面积为4πR2 4π (2 3)2
2
如图 2,分别取 AA1 , A1C1 , B1C1 的中点为 E,F,G,连接 FG,EP,EF,PG.
48π .
因为 F,G 分别为 AC , BC 的中点,所以 FG ∥ A B 且 FG 1 A B 2 2 .
1 1 1 1
在直三棱柱 ABC A1B1C1 中, AA1
1 1
BB1 且 AA1 BB1 .
2 1 1
因为 E,P 分别为 AA1 , BB1 的中点,所以 A1E∥B1P 且 A1E B1P ,所以四边形 A1B1PE 为平行四边形,所以
PE∥ A B 且PE AB,所以 FG PE ,且 FG 1 PE ,所以 P,E,F,G 四点共面.
1 1 1 1 2
因为 E,F 分别为 AA1 , A1C1 的中点,所以 EF ∥ AC1 .
又 EF 平面PEFG , AC1 平面PEFG ,所以 AC1 ∥平面PEFG . 因为 A1C1 B1C1 且 F,G 分别为 A1C1, B1C1 的中点,所以 A1F B1G ,
则 EF
PG 2 2 ,所以四边形 PEFG 即为符合要求的等腰梯形.
当 E 不是 AA1 的中点时,PE 不平行平面 A1B1C1 ,则四边形 PEFG 不是等腰梯形,故等腰梯形有且仅有一个.在等腰梯形 PEFG 中, FG EF PG 2 2 , EP 4 2 .
过点 G 作 EP 的垂线,交 EP 于点 H,
所以GH
6, S
梯形PEFG
1 (2 2 4 2) 6 .
2
故答案为: 48π ; 6
15.(1)函数 f (x) 的定义域为( 1,1) ;
(2) 2 .
1 x 0
( )根据函数解析式,得
1 x 0
,解出不等式,取交集即可;
(2)通过计算 f ( x) ,并与 f (x) 比较,即可判断奇偶性,根据奇偶性,即可求得 f ( t) .
【详解】(1)由题意, f (x) lg(1 x) lg(1 x) ,
由 1 x 0 ,解得 1 x 1,
1 x 0
则函数 f (x) 的定义域为M 1,1 .
(2)由(1)知函数 f (x) 的定义域关于原点对称.
又 f ( x) lg(1 x) lg(1 x) lg 1 x lg 1 x f x ,所以函数 f (x) 为奇函数,
又 f (t) 2 ,所以 f ( t) f (t) 2 .
16.(1) b 3, 6 ,→ 2, 1
(2) 3 10
10
根据两平行向量、垂直向量的坐标关系列方程求解;
求出2a 、b → 的坐标,直接代入向量夹角公式中求余弦值即可.
【详解】(1)因为 → ,所以 x 2 3 6 ,则b 3, 6 ,因为a ⊥c ,所以2 2 y 0 y 1 ,则→ 2, 1 .
(2)因为2a (2, 4) , b → (5, 5) ,
→ → →
→ → → 2a b c 10 20 3
所以cos 2a, b c → → → ,
a b c
10
即向量2a 与向量b → 的夹角的余弦值为 3 10 .
c 10
17.(1) 3
2
(2)( 3, 2 3úù
选①,由正弦定理和同角三角函数关系得到tan C
形面积公式进行求解;
3 ,故C π ,由余弦定理得到a 1 ,利用三角
3
选②,由余弦定理求出C π , a 1 ,由三角形面积公式求出答案;
3
解法一:由余弦定理和基本不等式得到a b 2
,结合三角形的三边关系可知a b c
3 ,从而
求出a b 的取值范围;
解法二:由正弦定理得到a 2 sin A, b 2 sin B ,结合三角恒等变换得到a b 2 3 sin A π ,结合
6
A π π , 5π ,求出
2 3 sin A 2 3 ,得到答案.
6 6 6 6
【详解】(1)选条件①:由正弦定理,得sin C sin A 3 sin A cos C .因为 A (0, π),所以sin A 0 ,
所以sin C 3 cos C ,得tan C 3 .
因为C (0, π) ,所以C π .
3
在V ABC 中,当c
3, b 2, C π 时,
3
由余弦定理c2 a2 b2 2ab cos C ,
得3 a2 4 2 a 2 1 ,即a2 2a 1 0 ,所以a 1 ,
2
所以S
1 ab sin C 1 1 2 sin π 3 .
△ ABC
2 2 3 2
选条件②:因为(a b)2 c2 ab ,整理得a2 b2 c2 ab .
a2 b2 c2 ab 1
由余弦定理,得cos C .
2ab
因为C (0, π) ,所以C π .
3
2ab 2
在V ABC 中,当c
3, b 2, C π 时,
3
由余弦定理c2 a2 b2 2ab cos C ,
得3 a2 4 2 a 2 1 ,即a2 2a 1 0 ,所以a 1 ,
2
所以S
1 ab sin C 1 1 2 sin π 3 .
△ ABC
2 2 3 2
(2)解法一:由题设及(1)可知C π , c 3 .
3
由余弦定理,得( 3)2 a2 b2 2ab cos π a2 b2 ab ,
3
a b 2
化简得(a b)2 3 3ab .又ab ,
2
所以(a b)2 3 3ab 3 (a b)2 ,
4
解得a b 2 ,
当且仅当a b c 时等号成立,
由三角形的三边关系可知a b c 3 ,
所以
a b 2
,即a b 的取值范围为 3, 2 3 .
解法二:由题设及(1)可知C π , c 3 .
3
a
由正弦定理,得sin A
b
sin B
c
sin C
3 2
3 ,
2
所以a 2 sin A, b 2 sin B ,
得a b 2(sin A sin B) 2 sin A sin A π
3
π π
3 3
2 sin A sin A cos 3 cos Asin 3 2 2 sin A 2 cos A
2 3 3 sin A 1 cos A 2 3 sin A π ,
2 2
6
因为C π ,则 A π π , 5π ,
π 1
所以sin A ,1 ,
故
2 3 sin A π 2 3 ,
6
所以
a b 2
,即a b 的取值范围为 3, 2 3 .
18.(1) a 0.025
(2)69.50;71.67 (3)32
根据频率直方图中各小矩形的面积之和为 1,列式求解;
根据频率直方图估算平均数公式,百分位数定义列式求解;
根据分层抽样的抽样比公式,结合总体方差运算公式进行求解即可.
【详解】(1)10 (0.005 a 0.045 0.020 0.005) 1 ,解得a 0.025 .
(2)由频率分布直方图易知每组的频率依次为0.05, 0.25, 0.45, 0.20, 0.05 ,所以这 100 名候选者面试成绩的平均数约为
50 0.05 60 0.25 70 0.45 80 0.20 90 0.05 69.50 .
因为0.05 0.25 0.30 0.60, 0.05 0.25 0.45 0.75 0.60 ,
设这 100 名候选者面试成绩的第 60 百分位数为 x,则 x [65, 75) ,则0.05 0.25 (x 65) 0.045 0.60 ,解得 x 71.67 ,
故第 60 百分位数为71.67 .
(3)设第四组、第五组面试者的面试成绩的平均数与方差分别为 x , x , s2 , s2 ,
且两组频率之比为 0.20 4 ,
0.05 1
则第四组和第五组所有面试者的面试成绩的平均数为 x 4 80 1 90 82 ,
5 5
第四组和第五组所有面试者的面试成绩的方差为
s2 4 s2 x x 2 1 s2 x x 2 4 15 (80 82)2 1 20 (90 82)2 32 ,
5 1 1
5 2 2
5
5
故估计第四组和第五组所有面试者的面试成绩的方差是 32. 19.(1)证明见解析
证明见解析
sinθ 2 3 3
证法一:根据平行四边形性质以及线面平行的判定,可得答案;证法二:利用中位线性质以及线面平行判定,可得面面平行,根据面面平行的性质,可得答案.
根据菱形以及线面垂直的性质,可得线线垂直,利用线面垂直判定,可得答案.
利用等体积法,选定三棱锥,根据解三角形的思路,表示高与底,建立函数,可得答案.
【详解】(1)证法一:如图 1,取 PB 的中点为 Q,连接 EQ,CQ.
又 E,F 分别为线段 PA,DC 的中点,四边形 ABCD 为菱形,
所以 FC / / AB 且FC
1 AB, EQ / / AB 且 EQ 1 AB ,
2 2
所以 FC / / EQ 且 FC EQ ,所以四边形 EFCQ 为平行四边形,所以 EF / /CQ .又 EF 平面 PBC , CQ 平面 PBC,所以 EF / / 平面 PBC.
证法二:如图 2,取 PD 的中点为 G,连接 EG,FG.
由中位线性质,可得 EG / / AD ,且 AD / / BC ,所以 EG / / BC .又 EG 平面 PBC , BC 平面 PBC,所以 EG / / 平面 PBC.同理可证 FG / / 平面 PBC.
又 EG ∩ FG G , EG 平面 EFG , FG 平面 EFG,所以平面 EFG / / 平面 PBC.
又 EF 平面 EFG,所以 EF / / 平面 PBC.
证明:如图 3,连接 AC,BD.
因为四边形 ABCD 为菱形,所以 AC ⊥BD .
因为 PD 平面 ABCD , AC 平面 ABCD,所以 PD AC .
又 BD 平面 PBD , PD 平面 PBD, BD ∩ PD D ,所以 AC 平面 PBD.
设 AD a, a 0 .
因为四边形 ABCD 为菱形,而∠DAB 60 ,故 BD AB AD a .
因为 PD 平面 ABCD , AD 平面 ABCD , CD 平面 ABCD , BD 平面 ABCD,故 PD AD, PD CD, PD BD .
又因为 PD 2 ,故 PA PC PB .
而 AB = a ,故S
1 a
1 a
3 a2 4 .
△PAB
2 2 4
设 d 为点 C 到平面 PAB 的距离,
所以V 1 S
d 1 1 a 3 a2 4 d .
C PAB 3
△PAB
3 2 4
又V 1 S
PD 2 S
2 3 a2 3 a2 .
P ABC 3 △ABC
3 △ABC
3 4 6
由等体积法,有V V ,故 1 1 a
3 a2 4 d 3 a2 ,
C PAB P ABC
d
解得 .
3 2 4 6
而 PC 与平面 PAB 所成的角为θ,所以sinθ d d
PC
1 2
2 2
2 2
2 2 3 3 ,
1
当且仅当a4 64 ,即a 64 4 时等号成立,所以sinθ 2
3 .
max
数学试卷
一、单选题
已知集合M x 1 x 4 , N x x 2 0 ,则 M ∩ N ( )
( 1, 4]
( 1, 4)
(2, 4) D. (2, 4]
样本数据 2,3,6,8,9,10 的中位数是( )
A.6 B.7 C.8 D.9
在V ABC 中,E 为边 BC 上的一点,且 BE 3EC ,则 AE ( )
1 –––→
AB
3 –––→
AC
3 –––→
AB
1 –––→
AC
4 4 4 4
3 –––→
AB
5 –––→
AC
1 –––→
AB
2 –––→
AC
8 8 3 3
从 0~9 这 10 个数中随机选择一个数,则事件“这个数平方的个位上的数字是 6”的概率为( )
A. 1
10
B. 1
5
C. 3
10
D. 2
5
已知圆台上底面半径为 1,下底面半径为 2,母线长为 2,则圆台的体积为( )
3 3π B. 8 3π
3
7 3π
3
2 3π
某校在校园科技节期间举办了“智能机器人挑战 ”,为了解高一年级 500 名学生观看比的情况,该校学生会用随机抽样的方式抽取了一个容量为 50 的样本进行调查,并将数据整理后,列表如下:
从表中可以得出正确的结论为( )
估计观看比场数的极差为 6 B.估计观看比场数的众数为 2
C.估计观看比不低于 4 场的学生约为 200 人 D.估计观看比不超过 2 场的学生概率为0.4
如图,某数学建模活动小组为了测量河对岸的塔高 AB ,选取与塔底 B 在同一平面的两个测量基点 C 与 D.现测量得 BCD 30 , BDC 120 , CD 10m ,在点 C 处测得塔顶 A 的仰角为 60°,则塔高 AB ( )
0m B. 20 3m C.30m D. 30 3m
函数 f (x) [x] 的函数值表示不超过 x 的最大整数,例如,[ 3.5] 4,[2.1] 2 ,则函数 g(x) x [x] 的
值域为( )
[0,1) B. (0,1] C. ( 1, 0)
D. ( 1,1]
二、多选题
已知复数 z 1 2i (i 是虚数单位),则下列说法正确的是( )
| z | B.z 的虚部是 2
复数 z 的共轭复数为z 1 2i
复数 z 在复平面内对应的点位于第四象限
已知事件 A,B 满足 P( A) 0.1, P(B) 0.6 ,则下列说法正确的是( )
事件 A 与事件 B 可能为对立事件
若事件 A 与事件 B 相互独立,则它们的对立事件也相互独立
若事件 A 与事件 B 互斥,则 P( A B) 0.7
若事件 A 与事件 B 相互独立,则 P( AB) 0.06
如图,在棱长为 2 的正方体 ABCD A1B1C1D1 中,M,N,P 分别是 BB1 , DD1, C1D1 的中点,Q 是侧面 BCC1B1
内的动点(含边界),则下列结论正确的是( )
A, B1 , P, N 四点共面
异面直线CD 与 BC 所成的角为 π
1 1 4
当点 Q 在线段 B1C 上运动时,三棱锥 A1 BDQ 的体积为定值
当 NQ 2
时,点 Q 的运动轨迹的长度为 2π
3
三、填空题
2
已知θ为锐角,且cosθ ,则tanθ .
3
在一次猜灯谜活动中,共有 10 道灯谜、甲、乙两名同学独立竞猜,甲同学猜对了 8 道,乙同学猜对了
4 道,假设猜对每道灯谜是等可能的.若任选一道灯谜,则恰有一人猜对的概率为 .
在《九章算术》中,底面是直角三角形的直三棱柱被称为“堑堵”.如图,三棱柱 ABC A1B1C1 为一“堑堵”,P 是 BB1 的中点, AA1 AC BC 4 ,则该“堑堵”的外接球的表面积为 ;在过点 P 且与直线 AC1
平行的截面中,当截面图形为等腰梯形时,该截面的面积为
四、解答题
已知函数 f (x) lg(1 x) lg(1 x) .
求函数 f (x) 的定义域 M;
判断函数 f (x) 的奇偶性,若 f (t) 2 ,求 f ( t) 的值.
已知平面向量 → (1, 2), b → (2, y) ,且 → → → .
求b 和c 的坐标;
求向量2a 与向量b → 的夹角的余弦值.
在V ABC 中, c ,再从下面两个条件中,选出一个作为已知条件,解答下面的问题.条件①:
c sin A 3a cos C ;条件②: (a b)2 c2 ab .
若b 2 ,求V ABC 的面积;
求a b 的取值范围.
18.2025 年 7 月,黔南州“铁人三项 ”在州府都匀市举行.志愿者的服务工作是比成功举办的重要保障,都匀市某单位承办了志愿者选拔的面试工作.现随机抽取 100 名候选者的面试成绩,并分成五组:第一组
45, 55 ,第二组 55, 65 ,第三组 65, 75 ,第四组 75,85 ,第五组 85, 95 ,绘制成如图所示的频率分布直方图.
求 a 的值.
估计这 100 名候选者面试成绩的平均数和第 60 百分位数(保留两位小数).
现从以上各组中用分层随机抽样的方法选取部分担任本市的宣传者.若这 100 名面试者中第四组面试者的面试成绩的平均数和方差分别为 80 和 15,第五组面试者的面试成绩的平均数和方差分别为 90 和 20,据此估计这次第四组和第五组所有面试者的面试成绩的方差.
19.如图,在四棱锥 P ABCD 中,底面 ABCD 为菱形, PD 底面 ABCD,E,F 分别为线段 PA,DC 的中点.
证明: EF // 平面 PBC;
证明: AC 平面 PBD;
若 PD 2, DAB 60 ,记 PC 与平面 PAB 所成的角为θ,求sinθ的最大值.
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A B C D C A AB BCD
题号 11
答案 ACD
1.D
根据集合的交集运算求解.
【详解】M ∩ N {x∣ 1 x 4}∩{x∣x 2 0} {x∣ 1 x 4}∩{x∣x 2} {x∣2 x 4} (2, 4] .故选:D.
2.B
根据中位数的定义求解.
【详解】因为样本数据个数是偶数,所以这组数据的中位数是第 3 位数和第 4 位数的平均数,
即 6 8 7 .
2
故选:B.
3.A
利用向量的线性运算,结合线段的比例关系来推导 AE 的表达式.
–––→ –––→ –––→ –––→
【详解】由图形可知: AE AB BE AB
3 –––→
BC
1 –––→
AB
3 –––→
AC .
故选:A 4.B
利用列举法求解出古典概型的概率.
4 4 4
【详解】从 0~9 这 10 个数中随机选择一个数,共有 10 种可能,其样本空间可表示为
{0,1, 2, 3, 4, 5, 6, 7,8, 9},
若一个数平方的个位上的数字是 6,则该数是 4 或 6,共 2 种情况,故所求概率为 2 1 .故 B 正确.
10 5
故选:B.
5.C
利用圆台体积公式即可求得结果.
【详解】设上、下底面的半径分别为r1 , r2 ,高为 h,母线l 2 ,
则S πr 2 π, S
πr 2 4π , h
3 ,
1 1 2 2
所以V 1 S
S
h 1 π
π 4π 4π 7 3π .
3
故选:C.
1
2 3 3
6.D
A 选项,利用极差的定义得到答案;B 选项,先求出m 16 ,比较频率得到众数为 1;C 选项,求出观看比 不低于 4 场的学生所占百分比,进而求出学生约为 220 人;D 选项,计算出观看比不超过 2 场的学生频率,进而判断 D 选项.
【详解】A 选项,由表可知,估计观看比场数的极差为7 0 7 ,A 错误; B 选项,由频率分布表的性质,得m 100 7 18 15 10 14 15 5 16 . 由表知,出现频率最高的场数为 1,所以众数为 1,B 错误;
C 选项,因为观看比不低于 4 场的学生所占百分比为10% 14% 15% 5% 44% ,所以估计观看比不低于 4 场的学生约为500 44% 220 (人),C 错误;
D 选项,估计观看比不超过 2 场的学生概率为7% 18% 15% 40% 0.4 ,D 正确.故选:D.
7.C
在△BCD 中,由正弦定理求得 BC 10 3 ,在Rt△ABC 中,解直角三角形得解.
【详解】在△BCD 中,由三角形内角和定理,
得 CBD 180 BDC BCD 180 120 30 30 .
由正弦定理,得
BC
sin BDC
CD
sin CBD
,即 BC
sin120
10
sin 30
,解得 BC 10 3 .
在Rt△ABC 中, AB BC tan 60 10 3 30 ,即塔高 AB 30m .故选:C.
8.A
根据取整函数的定义求函数的值域.
【详解】设 x a b ,其中a x , b 为 x 的小数部分,则0 b 1 ,则 g(x) x [x] b 0,1 ,
所以函数 g(x) 的值域为: 0,1 .
故选:A
AB
对 A,利用复数模公式求解;对 B,根据复数虚部概念判断;对 C,根据共轭复数的定义判断;对 D,根据复数的几何意义判断.
【详解】对于 A, | z | 5 ,故 A 正确;
对于 B,复数 z 1 2i 的虚部为 2,故 B 正确;
对于 C,复数 z 1 2i 的共轭复数为 z 1 2i ,故 C 错误;
对于 D,因为复数 z 在复平面内对应的点的坐标为( 1, 2) ,则复数 z 在复平面内对应的点位于第二象限,故
D 错误.
故选:AB.
BCD
利用事件的对立可对 A 判断;由利用相互独立事件的定义,可对 B 判断;利用互斥事件的概率公式,即可对 C 判断;利用相互独立事件的概率公式即可对 D 判断.
【详解】对于 A,由对立事件的概率和为 1,但 P( A) P(B) 0.7 1,故 A 错误;
对于 B,根据相互独立事件的性质可得事件A 与事件 B 相互独立,则它们的对立事件也相互独立,故 B 正确;
对于 C,若事件A 与事件 B 互斥,则 P( A B) P( A) P(B) 0.7 ,故 C 正确;
对于 D,根据相互独立事件的定义, P( AB) P( A)P(B) 0.06 ,故 D 正确.故选:BCD.
ACD
对 A,由题可得 AB1 / / DC1 ,PN / / DC1 ,得 AB1 / / PN 得证;对 B,连接 AD1 , CD1 , AC, BC1 ,可得异面直线CD1
与 BC1 所成的角为 AD1C ,求解判断;对 C,由等体积法,可得VA BDQ VQ A BD ,求解判断;对 D,由题可得点 Q 的运动轨迹是在侧面 BCC1B1 内以CC1 的中点为圆心,半径r 2 的圆弧 H MG ,求解判断.
【详解】对于 A,如图 1,在正方体中,易知 AB1 / / DC1 .
又 P,N 分别是C1D1 , DD1 的中点,则 PN / / DC1 ,所以 AB1 / / PN ,即 A, B1 , P, N 四点共面,故 A 正确;对于 B,如图 2,分别连接 AD1 , CD1 , AC, BC1 ,由题意,易知 BC1 / / AD1 ,
则异面直线CD 与 BC 所成的角为 AD C ,易知VAD C 为等边三角形,故 AD C π ,故 B 错误;
1 1 1 1 1 3
对于 C,如图 3,由等体积法,得VA BDQ VQ A BD .
因为 B1C / / A1D ,可得 B1C / / 平面 A1BD ,又点 Q 在线段 B1C 上运动,所以点 Q 到平面 A1BD 的距离为定值.又S△A BD 也为定值,
所以VQ A BD 为定值,即VA BDQ VQ A BD 为定值,
1 1 1
且V V V V
1 S
AA 1 1 2 2 2 4 ,故 C 正确;
A1 BDQ Q A1BD C A1BD A1 BCD
3 △BCD
1 3 2 3
对于 D,如图 4,取CC1 的中点O ,易得ON 平面 BCC1B1 ,
当 NQ 2
时,点 Q 的运动轨迹是在侧面 BCC1B1 内以CC1 的中点O 为圆心,半径r 2 的圆弧 H MG ,
在RtVOC H 中,由OH 2 , C O 1 ,可得 C OH π ,同理, GOC π ,
1 1 1 3 3
所以圆弧 H MG 圆心角为α π ,所以点 Q 的运动轨迹的长度为l αr π 2 2π ,故 D 正确.
3 3 3
故选:ACD.
12. 5
2
根据sin2θ cos2θ 1,且θ为锐角,推出sinθ
sinθ
1 cos2 θ,根据tanθ 即可求解.
cos
【详解】因为θ为锐角,且cosθ 2 ,所以sinθ
3
1 cos2θ
5 ,
3
故tanθ sinθ
cosθ
5
3 5 .
2 2
3
故答案为: 5 .
2
14 /0.56
25
已知甲、乙两人猜灯谜的独立事件恰有一人猜对的概率 P, 设事件 A 表示“甲猜对”,事件 B 表示“乙猜对”,则
P P( AB ∪ AB) P( A)P(B) P( A)P(B) .
【详解】设事件 A 表示“甲猜对”,事件 B 表示“乙猜对”,则 P( A) 8 4 , P(B) 4 2 ,
所以任选一道灯谜,恰有一个人猜对的概率为:
10 5
10 5
P( AB AB) P( A)P(B) P( A)P(B) 4 1 2 1 4 2 14 .
5 5 5 5 25
故答案为: 14 .
25
48π 6
①如图 1,把原三棱柱补成正方体,则正方体对角线为外接球的一条直径,根据2R 求
出半径,再根据面积公式S 4πR2 求解.
②如图 2,取中点 E,F,G 构造面 FGPE ,由 EF 与 AC1 线线平行推出 AC1 与面 FGPE 平行,根据边长关系进一步推出四边形 FGPE 即为唯一的等腰梯形,求其面积即可.
【详解】如图 1,将三棱柱 ABC A1B1C1 补成正方体 ACBQ A1C1B1Q1 ,
则外接球的半径 R 2 3 ,则外接球的表面积为4πR2 4π (2 3)2
2
如图 2,分别取 AA1 , A1C1 , B1C1 的中点为 E,F,G,连接 FG,EP,EF,PG.
48π .
因为 F,G 分别为 AC , BC 的中点,所以 FG ∥ A B 且 FG 1 A B 2 2 .
1 1 1 1
在直三棱柱 ABC A1B1C1 中, AA1
1 1
BB1 且 AA1 BB1 .
2 1 1
因为 E,P 分别为 AA1 , BB1 的中点,所以 A1E∥B1P 且 A1E B1P ,所以四边形 A1B1PE 为平行四边形,所以
PE∥ A B 且PE AB,所以 FG PE ,且 FG 1 PE ,所以 P,E,F,G 四点共面.
1 1 1 1 2
因为 E,F 分别为 AA1 , A1C1 的中点,所以 EF ∥ AC1 .
又 EF 平面PEFG , AC1 平面PEFG ,所以 AC1 ∥平面PEFG . 因为 A1C1 B1C1 且 F,G 分别为 A1C1, B1C1 的中点,所以 A1F B1G ,
则 EF
PG 2 2 ,所以四边形 PEFG 即为符合要求的等腰梯形.
当 E 不是 AA1 的中点时,PE 不平行平面 A1B1C1 ,则四边形 PEFG 不是等腰梯形,故等腰梯形有且仅有一个.在等腰梯形 PEFG 中, FG EF PG 2 2 , EP 4 2 .
过点 G 作 EP 的垂线,交 EP 于点 H,
所以GH
6, S
梯形PEFG
1 (2 2 4 2) 6 .
2
故答案为: 48π ; 6
15.(1)函数 f (x) 的定义域为( 1,1) ;
(2) 2 .
1 x 0
( )根据函数解析式,得
1 x 0
,解出不等式,取交集即可;
(2)通过计算 f ( x) ,并与 f (x) 比较,即可判断奇偶性,根据奇偶性,即可求得 f ( t) .
【详解】(1)由题意, f (x) lg(1 x) lg(1 x) ,
由 1 x 0 ,解得 1 x 1,
1 x 0
则函数 f (x) 的定义域为M 1,1 .
(2)由(1)知函数 f (x) 的定义域关于原点对称.
又 f ( x) lg(1 x) lg(1 x) lg 1 x lg 1 x f x ,所以函数 f (x) 为奇函数,
又 f (t) 2 ,所以 f ( t) f (t) 2 .
16.(1) b 3, 6 ,→ 2, 1
(2) 3 10
10
根据两平行向量、垂直向量的坐标关系列方程求解;
求出2a 、b → 的坐标,直接代入向量夹角公式中求余弦值即可.
【详解】(1)因为 → ,所以 x 2 3 6 ,则b 3, 6 ,因为a ⊥c ,所以2 2 y 0 y 1 ,则→ 2, 1 .
(2)因为2a (2, 4) , b → (5, 5) ,
→ → →
→ → → 2a b c 10 20 3
所以cos 2a, b c → → → ,
a b c
10
即向量2a 与向量b → 的夹角的余弦值为 3 10 .
c 10
17.(1) 3
2
(2)( 3, 2 3úù
选①,由正弦定理和同角三角函数关系得到tan C
形面积公式进行求解;
3 ,故C π ,由余弦定理得到a 1 ,利用三角
3
选②,由余弦定理求出C π , a 1 ,由三角形面积公式求出答案;
3
解法一:由余弦定理和基本不等式得到a b 2
,结合三角形的三边关系可知a b c
3 ,从而
求出a b 的取值范围;
解法二:由正弦定理得到a 2 sin A, b 2 sin B ,结合三角恒等变换得到a b 2 3 sin A π ,结合
6
A π π , 5π ,求出
2 3 sin A 2 3 ,得到答案.
6 6 6 6
【详解】(1)选条件①:由正弦定理,得sin C sin A 3 sin A cos C .因为 A (0, π),所以sin A 0 ,
所以sin C 3 cos C ,得tan C 3 .
因为C (0, π) ,所以C π .
3
在V ABC 中,当c
3, b 2, C π 时,
3
由余弦定理c2 a2 b2 2ab cos C ,
得3 a2 4 2 a 2 1 ,即a2 2a 1 0 ,所以a 1 ,
2
所以S
1 ab sin C 1 1 2 sin π 3 .
△ ABC
2 2 3 2
选条件②:因为(a b)2 c2 ab ,整理得a2 b2 c2 ab .
a2 b2 c2 ab 1
由余弦定理,得cos C .
2ab
因为C (0, π) ,所以C π .
3
2ab 2
在V ABC 中,当c
3, b 2, C π 时,
3
由余弦定理c2 a2 b2 2ab cos C ,
得3 a2 4 2 a 2 1 ,即a2 2a 1 0 ,所以a 1 ,
2
所以S
1 ab sin C 1 1 2 sin π 3 .
△ ABC
2 2 3 2
(2)解法一:由题设及(1)可知C π , c 3 .
3
由余弦定理,得( 3)2 a2 b2 2ab cos π a2 b2 ab ,
3
a b 2
化简得(a b)2 3 3ab .又ab ,
2
所以(a b)2 3 3ab 3 (a b)2 ,
4
解得a b 2 ,
当且仅当a b c 时等号成立,
由三角形的三边关系可知a b c 3 ,
所以
a b 2
,即a b 的取值范围为 3, 2 3 .
解法二:由题设及(1)可知C π , c 3 .
3
a
由正弦定理,得sin A
b
sin B
c
sin C
3 2
3 ,
2
所以a 2 sin A, b 2 sin B ,
得a b 2(sin A sin B) 2 sin A sin A π
3
π π
3 3
2 sin A sin A cos 3 cos Asin 3 2 2 sin A 2 cos A
2 3 3 sin A 1 cos A 2 3 sin A π ,
2 2
6
因为C π ,则 A π π , 5π ,
π 1
所以sin A ,1 ,
故
2 3 sin A π 2 3 ,
6
所以
a b 2
,即a b 的取值范围为 3, 2 3 .
18.(1) a 0.025
(2)69.50;71.67 (3)32
根据频率直方图中各小矩形的面积之和为 1,列式求解;
根据频率直方图估算平均数公式,百分位数定义列式求解;
根据分层抽样的抽样比公式,结合总体方差运算公式进行求解即可.
【详解】(1)10 (0.005 a 0.045 0.020 0.005) 1 ,解得a 0.025 .
(2)由频率分布直方图易知每组的频率依次为0.05, 0.25, 0.45, 0.20, 0.05 ,所以这 100 名候选者面试成绩的平均数约为
50 0.05 60 0.25 70 0.45 80 0.20 90 0.05 69.50 .
因为0.05 0.25 0.30 0.60, 0.05 0.25 0.45 0.75 0.60 ,
设这 100 名候选者面试成绩的第 60 百分位数为 x,则 x [65, 75) ,则0.05 0.25 (x 65) 0.045 0.60 ,解得 x 71.67 ,
故第 60 百分位数为71.67 .
(3)设第四组、第五组面试者的面试成绩的平均数与方差分别为 x , x , s2 , s2 ,
且两组频率之比为 0.20 4 ,
0.05 1
则第四组和第五组所有面试者的面试成绩的平均数为 x 4 80 1 90 82 ,
5 5
第四组和第五组所有面试者的面试成绩的方差为
s2 4 s2 x x 2 1 s2 x x 2 4 15 (80 82)2 1 20 (90 82)2 32 ,
5 1 1
5 2 2
5
5
故估计第四组和第五组所有面试者的面试成绩的方差是 32. 19.(1)证明见解析
证明见解析
sinθ 2 3 3
证法一:根据平行四边形性质以及线面平行的判定,可得答案;证法二:利用中位线性质以及线面平行判定,可得面面平行,根据面面平行的性质,可得答案.
根据菱形以及线面垂直的性质,可得线线垂直,利用线面垂直判定,可得答案.
利用等体积法,选定三棱锥,根据解三角形的思路,表示高与底,建立函数,可得答案.
【详解】(1)证法一:如图 1,取 PB 的中点为 Q,连接 EQ,CQ.
又 E,F 分别为线段 PA,DC 的中点,四边形 ABCD 为菱形,
所以 FC / / AB 且FC
1 AB, EQ / / AB 且 EQ 1 AB ,
2 2
所以 FC / / EQ 且 FC EQ ,所以四边形 EFCQ 为平行四边形,所以 EF / /CQ .又 EF 平面 PBC , CQ 平面 PBC,所以 EF / / 平面 PBC.
证法二:如图 2,取 PD 的中点为 G,连接 EG,FG.
由中位线性质,可得 EG / / AD ,且 AD / / BC ,所以 EG / / BC .又 EG 平面 PBC , BC 平面 PBC,所以 EG / / 平面 PBC.同理可证 FG / / 平面 PBC.
又 EG ∩ FG G , EG 平面 EFG , FG 平面 EFG,所以平面 EFG / / 平面 PBC.
又 EF 平面 EFG,所以 EF / / 平面 PBC.
证明:如图 3,连接 AC,BD.
因为四边形 ABCD 为菱形,所以 AC ⊥BD .
因为 PD 平面 ABCD , AC 平面 ABCD,所以 PD AC .
又 BD 平面 PBD , PD 平面 PBD, BD ∩ PD D ,所以 AC 平面 PBD.
设 AD a, a 0 .
因为四边形 ABCD 为菱形,而∠DAB 60 ,故 BD AB AD a .
因为 PD 平面 ABCD , AD 平面 ABCD , CD 平面 ABCD , BD 平面 ABCD,故 PD AD, PD CD, PD BD .
又因为 PD 2 ,故 PA PC PB .
而 AB = a ,故S
1 a
1 a
3 a2 4 .
△PAB
2 2 4
设 d 为点 C 到平面 PAB 的距离,
所以V 1 S
d 1 1 a 3 a2 4 d .
C PAB 3
△PAB
3 2 4
又V 1 S
PD 2 S
2 3 a2 3 a2 .
P ABC 3 △ABC
3 △ABC
3 4 6
由等体积法,有V V ,故 1 1 a
3 a2 4 d 3 a2 ,
C PAB P ABC
d
解得 .
3 2 4 6
而 PC 与平面 PAB 所成的角为θ,所以sinθ d d
PC
1 2
2 2
2 2
2 2 3 3 ,
1
当且仅当a4 64 ,即a 64 4 时等号成立,所以sinθ 2
3 .
max
同课章节目录
