苏教版六年级数学上册第一单元 长方体和正方体能力提优(B卷)(含答案)
文档属性
| 名称 | 苏教版六年级数学上册第一单元 长方体和正方体能力提优(B卷)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 176.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 17:32:47 | ||
图片预览



文档简介
第一单元能力提优(B卷)
关键能力提优
考试时间:80分钟 满分:100分
一、计算题。(共24分)
1.直接写出得数。(每题1分,共9分)
0.72÷0.8= 3.5-0.7= 0.36+0.4=
2.5÷0.125÷8=
2.计算下面各题,能简算的要简算。(每题2分,共8分)
98×99
7.3÷0.25+2.7×4 1.8×4.65+3.5×0.18
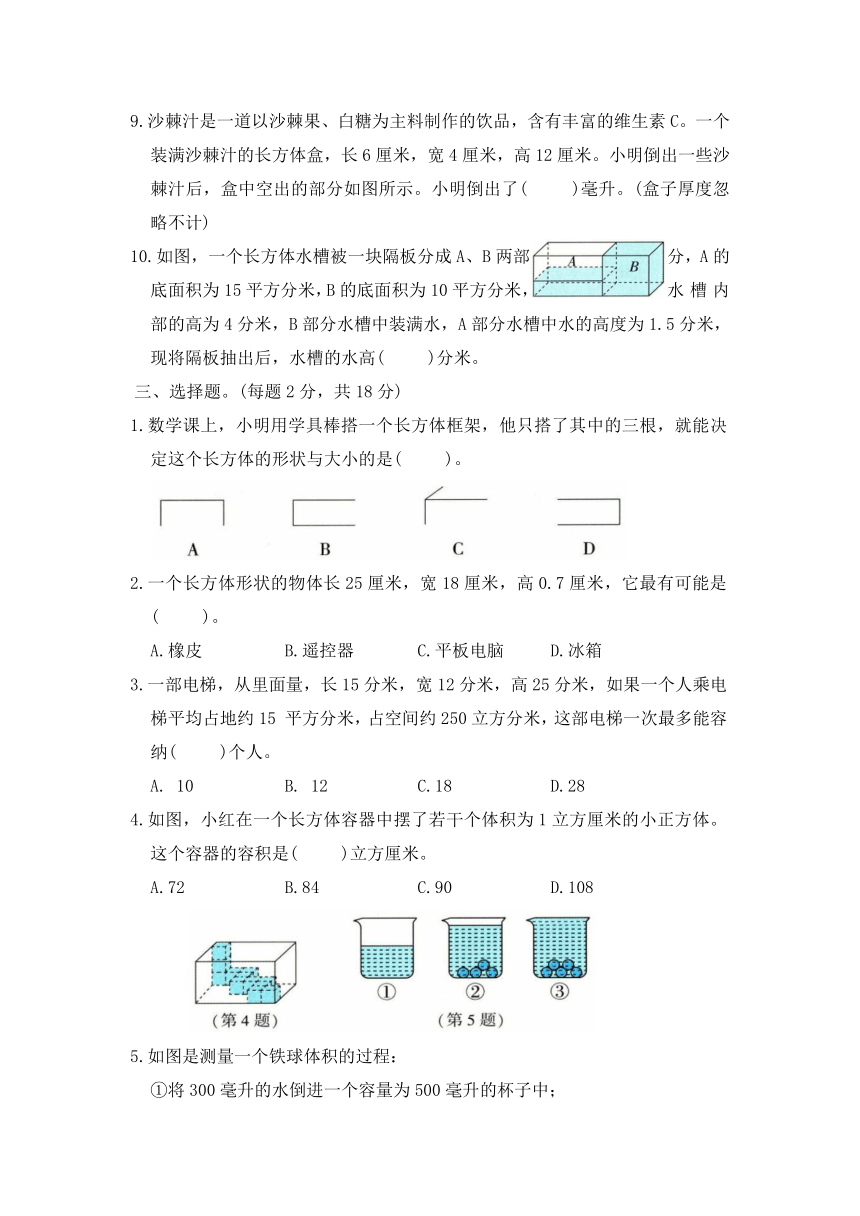
3.从下面选出几个图形,围成一个长方体,算一算你围成的长方体的表面积和体积。(单位:cm)(7分)
我选择的是( )。
解答:
二、填空题。(第1题4分,第6题3分,其余每题2分,共23分)
1.在 里填上“>”“<”或“=”。
7.8升 7.8立方米 5.7平方米 5700平方分米
4060毫升 4.06升 2.9立方厘米 2900立方分米
2.一根铁丝长72厘米,如果做成一个宽和高都是4厘米的长方体框架(无剩余),长是( )厘米;如果做成一个正方体框架,再在各个面蒙上一层硬纸板,需要( )平方厘米的硬纸板(铁丝无剩余,纸板粘贴处忽略不计)。
3.一个正方体玩具,它的平面展开图如图所示,原正方体中相对面上的两个数字之和为10,则 xy=( )。
4.把一个长6分米、宽5.5分米、高4分米的长方体,截成两个完全相同的小长方体,表面积最多增加( )平方分米,最少增加( )平方分米。≥举一反三
5.最少要用( )个棱长是2厘米的小正方体,可以拼成一个大正方体,拼好后大正方体的表面积比所有小正方体的表面积和减少( )平方厘米。
6.竹编有着悠久的历史,是国家级非物质文化遗产中的技艺之一。李奶奶用竹子编制了一个无盖收纳盒,从前面和左面看到的均如图所示。
(1)这个收纳盒的体积是( )立方分米,表面积是( )平方分米。
(2)如果里面放棱长是3厘米的盒子,最多能放( )个。
7.一张宽16厘米的长方形铁皮,在它的四个角分别剪去边长3厘米的正方形(如图),然后将剩下的部分折弯焊成一个无盖的长方体铁皮盒(焊接处损耗忽略不计)。如果这个铁皮盒的容积是840 毫升,那么它的底面积是( )平方厘米,原来这块长方形铁皮的面积是( )平方厘米。
8.一个长方体,如果从上部截去一个高3厘米的小长方体,就变成了一个正方体。这时表面积比原来减少60平方厘米。原来长方体的体积是( )立方厘米。举一反三
9.沙棘汁是一道以沙棘果、白糖为主料制作的饮品,含有丰富的维生素C。一个装满沙棘汁的长方体盒,长6厘米,宽4厘米,高12厘米。小明倒出一些沙棘汁后,盒中空出的部分如图所示。小明倒出了( )毫升。(盒子厚度忽略不计)
10.如图,一个长方体水槽被一块隔板分成A、B两部分,A的底面积为15平方分米,B的底面积为10平方分米,水槽内部的高为4分米,B部分水槽中装满水,A部分水槽中水的高度为1.5分米,现将隔板抽出后,水槽的水高( )分米。
三、选择题。(每题2分,共18分)
1.数学课上,小明用学具棒搭一个长方体框架,他只搭了其中的三根,就能决定这个长方体的形状与大小的是( )。
2.一个长方体形状的物体长25厘米,宽18厘米,高0.7厘米,它最有可能是( )。
A.橡皮 B.遥控器 C.平板电脑 D.冰箱
3.一部电梯,从里面量,长15分米,宽12分米,高25分米,如果一个人乘电梯平均占地约15 平方分米,占空间约250立方分米,这部电梯一次最多能容纳( )个人。
A. 10 B. 12 C.18 D.28
4.如图,小红在一个长方体容器中摆了若干个体积为1立方厘米的小正方体。这个容器的容积是( )立方厘米。
A.72 B.84 C.90 D.108
5.如图是测量一个铁球体积的过程:
①将300毫升的水倒进一个容量为500毫升的杯子中;
②将四颗相同的铁球放入水中,结果水没有满;
③再将一颗同样的铁球放入水中,结果水满溢出。
根据以上过程,推测这样一个铁球的体积大约是( )立方厘米。
A.30~40 B.40~50 C.50~60 D.60~70
6.将42个棱长为1厘米的小正方体黏在一起拼成一个长方体,若长方体的底面周长为18厘米,则长方体的高是( )厘米。
A.2 B.3 C.4 D.7
7.在如图所示放在墙角的小正方体组合体中去掉一个小正方体,露在外面的面积减少48平方厘米,如果每个小正方体的棱长为4 厘米,那么去掉的小正方体是( )。
A.① B.② C.③ D.④
8.将一个表面涂色的正方体分割成若干个体积为1立方厘米的小正方体,其中两面涂色的有36块,原来正方体的体积是( )立方厘米。
A.64 B.125 C.216 D.8
9.(多选题)下面说法中不正确的是( )。
A.物体A比物体B的体积大,那么物体A的容积一定比物体B的容积大
B.正方体的棱长扩大到原来的3倍,则体积扩大到原来的27倍
C.如果一个长方体和一个正方体的底面周长相等,高也相等,那么体积也相等
D.如果一个长方体相邻的2个面是正方形,那么这个长方体一定是正方体
四、探究题。(3+3=6分)
1.用右图中的两个完全一样的三棱柱可以拼成一个长方体(四棱柱),图中一个三棱柱的体积是长方体体积的( ),长方体的体积=长方体的底面积×高,那么三棱柱的体积=( ),也就是( )的底面积×( )。
2.按照第1题的方法思考,尝试解决下面的问题。游泳中心的室内泳池如右图。小诺和瑞瑞对“泳池的容积是多少立方米 ”这个问题展开了讨论,请根据她们的思考过程解决问题。
小诺:它不是一个长方体,但可以通过割或补的方法(如图①)变成长方体,所以它的容积在( )立方米和( )立方米之间。
瑞瑞:两个完全一样的泳池能拼成一个大长方体(如图②)。这样就能计算出它的容积是( )立方米。
五、解决问题。(4+6+6+4+5+4=29分)
1.VT5-U轻型坦克,是中国一型轻型无人化坦克。军军买了一款 VT5-U轻型坦克的模型,用一个长32厘米、宽25厘米、高20厘米的长方体硬纸箱包装。如果用包装带将箱子捆扎起来(如图),打结处共用28厘米,那么一共要用多少厘米包装带
2.开展书香校园能够为学生在校园内创建浓厚的阅读氛围以及阅读环境,某小学为每个班级制作一个长80厘米、宽60厘米、高150厘米的书架(如图,有背板),并且最下面一层有2个门板,门板高40厘米。
(1)这个书架所占空间有多少立方分米
(2)制作一个这样的书架需要木板多少平方分米 (木料的厚度和冗余忽略不计)
3.王叔叔在院子里用混凝土浇筑了一个无盖的长方体水槽(如图),从外面量,水槽长12分米、宽8分米、高5分米,混凝土厚1分米(包括底部)。
(1)这个水槽的容积是多少升
(2)王叔叔用防水涂料将水槽里外都粉刷一层,如果每平方分米涂料要1.5元,那么王叔叔至少要花多少元
4.把一块底面长为12厘米、宽为8厘米、高为20厘米的长方体铁块,浸没在一个棱长为4分米的正方体水槽里(水没有溢出)。原来的水面高为28厘米,放入铁块后水面高度为多少厘米
5.一个学习小组的四名同学观察并测量了一个长方体。
甲说:“这个长方体的棱长总和是64分米。”
乙说:“它的底面周长是24分米。”
丙说:“长方体的前、后、左、右四个面的面积之和是96平方分米。”
丁说:“如果高再增加2分米,它恰好是一个正方体。”
四人得到的数据都是正确的,请你筛选出必要的数据作为条件,求出这个长方体的体积。
6.浙江民间有着农历二月二吃撑腰糕的习俗,寓意强健筋骨,迎接新一年的挑战。如图是王师傅做的一块长方体的撑腰糕,前、后两个面是边长为4.5厘米的正方形,将其切成四块后表面积增加了440.5平方厘米。那么原长方体撑腰糕的体积是多少立方厘米
参考答案:
一、1.0.9 2.8 0.76 0.36 0.125 2.5 1
2.0 9702 40 9
3. ①③⑤⑥⑦⑧ 5×3×2+4×3×2+5×4×2=94(平方厘米)3×4×5=60(立方厘米)
二、1. < < = < 2.10 216
3.72 4.66 44 5.8 96
6.(1)6 16 (2)180
7.280 544 8.200 9.72
10.2.5
提示:先分别求出A、B部分水的体积,再求出水槽中水的总体积,最后求出隔板抽出后水槽的水高。B部分底面积为 10平方分米,水高为4分米,所以B部分水的体积为 10×4=40(立方分米),A部分底面积为15平方分米,水高为1.5分米,所以A部分水的体积为15×1.5=22.5(立方分米)。水槽中水的总体积为A部分水的体积加上 B部分水的体积,即40+22.5=62.5(立方分米),水槽的底面积为A部分和B部分底面积之和,即15+10=25(平方分米),所以隔板抽出后水槽的水高为62.5÷25=2.5(分米)。
三、1. C 2. C 3. B 4. C 5. B 6. B 7. A8. B 9. AC
四、1.一半 长方体的底面积×高÷2 三棱柱 高2. 1500 2000 1750
五、1. 32×2+25×4+20×6+28=312(厘米)
2. (1)80厘米=8分米 60厘米=6分米
150厘米=15分米 8×6×15=720(立方分米)
(2)40厘米=4分米
3. (1)12-1×2=10(分米) 8-1×2=6(分米)
5-1=4(分米)10×6×4=240(立方分米)=240升
(2)12×5×2+8×5×2+12×8×2+10×4×2+6×4×2=520(平方分米)
520×1.5=780(元)
4. 4分米=40厘米
12×8×20÷(40×40)+28=29.2(厘米)
5.答案不唯一,如:选乙、丁数据:
长、宽:24÷4=6(分米)
高:6-2=4(分米)
体积:6×6×4=144(立方分米)
6. (440.5-4.5×4.5×2)÷2×4.5=900(立方厘米)
关键能力提优
考试时间:80分钟 满分:100分
一、计算题。(共24分)
1.直接写出得数。(每题1分,共9分)
0.72÷0.8= 3.5-0.7= 0.36+0.4=
2.5÷0.125÷8=
2.计算下面各题,能简算的要简算。(每题2分,共8分)
98×99
7.3÷0.25+2.7×4 1.8×4.65+3.5×0.18
3.从下面选出几个图形,围成一个长方体,算一算你围成的长方体的表面积和体积。(单位:cm)(7分)
我选择的是( )。
解答:
二、填空题。(第1题4分,第6题3分,其余每题2分,共23分)
1.在 里填上“>”“<”或“=”。
7.8升 7.8立方米 5.7平方米 5700平方分米
4060毫升 4.06升 2.9立方厘米 2900立方分米
2.一根铁丝长72厘米,如果做成一个宽和高都是4厘米的长方体框架(无剩余),长是( )厘米;如果做成一个正方体框架,再在各个面蒙上一层硬纸板,需要( )平方厘米的硬纸板(铁丝无剩余,纸板粘贴处忽略不计)。
3.一个正方体玩具,它的平面展开图如图所示,原正方体中相对面上的两个数字之和为10,则 xy=( )。
4.把一个长6分米、宽5.5分米、高4分米的长方体,截成两个完全相同的小长方体,表面积最多增加( )平方分米,最少增加( )平方分米。≥举一反三
5.最少要用( )个棱长是2厘米的小正方体,可以拼成一个大正方体,拼好后大正方体的表面积比所有小正方体的表面积和减少( )平方厘米。
6.竹编有着悠久的历史,是国家级非物质文化遗产中的技艺之一。李奶奶用竹子编制了一个无盖收纳盒,从前面和左面看到的均如图所示。
(1)这个收纳盒的体积是( )立方分米,表面积是( )平方分米。
(2)如果里面放棱长是3厘米的盒子,最多能放( )个。
7.一张宽16厘米的长方形铁皮,在它的四个角分别剪去边长3厘米的正方形(如图),然后将剩下的部分折弯焊成一个无盖的长方体铁皮盒(焊接处损耗忽略不计)。如果这个铁皮盒的容积是840 毫升,那么它的底面积是( )平方厘米,原来这块长方形铁皮的面积是( )平方厘米。
8.一个长方体,如果从上部截去一个高3厘米的小长方体,就变成了一个正方体。这时表面积比原来减少60平方厘米。原来长方体的体积是( )立方厘米。举一反三
9.沙棘汁是一道以沙棘果、白糖为主料制作的饮品,含有丰富的维生素C。一个装满沙棘汁的长方体盒,长6厘米,宽4厘米,高12厘米。小明倒出一些沙棘汁后,盒中空出的部分如图所示。小明倒出了( )毫升。(盒子厚度忽略不计)
10.如图,一个长方体水槽被一块隔板分成A、B两部分,A的底面积为15平方分米,B的底面积为10平方分米,水槽内部的高为4分米,B部分水槽中装满水,A部分水槽中水的高度为1.5分米,现将隔板抽出后,水槽的水高( )分米。
三、选择题。(每题2分,共18分)
1.数学课上,小明用学具棒搭一个长方体框架,他只搭了其中的三根,就能决定这个长方体的形状与大小的是( )。
2.一个长方体形状的物体长25厘米,宽18厘米,高0.7厘米,它最有可能是( )。
A.橡皮 B.遥控器 C.平板电脑 D.冰箱
3.一部电梯,从里面量,长15分米,宽12分米,高25分米,如果一个人乘电梯平均占地约15 平方分米,占空间约250立方分米,这部电梯一次最多能容纳( )个人。
A. 10 B. 12 C.18 D.28
4.如图,小红在一个长方体容器中摆了若干个体积为1立方厘米的小正方体。这个容器的容积是( )立方厘米。
A.72 B.84 C.90 D.108
5.如图是测量一个铁球体积的过程:
①将300毫升的水倒进一个容量为500毫升的杯子中;
②将四颗相同的铁球放入水中,结果水没有满;
③再将一颗同样的铁球放入水中,结果水满溢出。
根据以上过程,推测这样一个铁球的体积大约是( )立方厘米。
A.30~40 B.40~50 C.50~60 D.60~70
6.将42个棱长为1厘米的小正方体黏在一起拼成一个长方体,若长方体的底面周长为18厘米,则长方体的高是( )厘米。
A.2 B.3 C.4 D.7
7.在如图所示放在墙角的小正方体组合体中去掉一个小正方体,露在外面的面积减少48平方厘米,如果每个小正方体的棱长为4 厘米,那么去掉的小正方体是( )。
A.① B.② C.③ D.④
8.将一个表面涂色的正方体分割成若干个体积为1立方厘米的小正方体,其中两面涂色的有36块,原来正方体的体积是( )立方厘米。
A.64 B.125 C.216 D.8
9.(多选题)下面说法中不正确的是( )。
A.物体A比物体B的体积大,那么物体A的容积一定比物体B的容积大
B.正方体的棱长扩大到原来的3倍,则体积扩大到原来的27倍
C.如果一个长方体和一个正方体的底面周长相等,高也相等,那么体积也相等
D.如果一个长方体相邻的2个面是正方形,那么这个长方体一定是正方体
四、探究题。(3+3=6分)
1.用右图中的两个完全一样的三棱柱可以拼成一个长方体(四棱柱),图中一个三棱柱的体积是长方体体积的( ),长方体的体积=长方体的底面积×高,那么三棱柱的体积=( ),也就是( )的底面积×( )。
2.按照第1题的方法思考,尝试解决下面的问题。游泳中心的室内泳池如右图。小诺和瑞瑞对“泳池的容积是多少立方米 ”这个问题展开了讨论,请根据她们的思考过程解决问题。
小诺:它不是一个长方体,但可以通过割或补的方法(如图①)变成长方体,所以它的容积在( )立方米和( )立方米之间。
瑞瑞:两个完全一样的泳池能拼成一个大长方体(如图②)。这样就能计算出它的容积是( )立方米。
五、解决问题。(4+6+6+4+5+4=29分)
1.VT5-U轻型坦克,是中国一型轻型无人化坦克。军军买了一款 VT5-U轻型坦克的模型,用一个长32厘米、宽25厘米、高20厘米的长方体硬纸箱包装。如果用包装带将箱子捆扎起来(如图),打结处共用28厘米,那么一共要用多少厘米包装带
2.开展书香校园能够为学生在校园内创建浓厚的阅读氛围以及阅读环境,某小学为每个班级制作一个长80厘米、宽60厘米、高150厘米的书架(如图,有背板),并且最下面一层有2个门板,门板高40厘米。
(1)这个书架所占空间有多少立方分米
(2)制作一个这样的书架需要木板多少平方分米 (木料的厚度和冗余忽略不计)
3.王叔叔在院子里用混凝土浇筑了一个无盖的长方体水槽(如图),从外面量,水槽长12分米、宽8分米、高5分米,混凝土厚1分米(包括底部)。
(1)这个水槽的容积是多少升
(2)王叔叔用防水涂料将水槽里外都粉刷一层,如果每平方分米涂料要1.5元,那么王叔叔至少要花多少元
4.把一块底面长为12厘米、宽为8厘米、高为20厘米的长方体铁块,浸没在一个棱长为4分米的正方体水槽里(水没有溢出)。原来的水面高为28厘米,放入铁块后水面高度为多少厘米
5.一个学习小组的四名同学观察并测量了一个长方体。
甲说:“这个长方体的棱长总和是64分米。”
乙说:“它的底面周长是24分米。”
丙说:“长方体的前、后、左、右四个面的面积之和是96平方分米。”
丁说:“如果高再增加2分米,它恰好是一个正方体。”
四人得到的数据都是正确的,请你筛选出必要的数据作为条件,求出这个长方体的体积。
6.浙江民间有着农历二月二吃撑腰糕的习俗,寓意强健筋骨,迎接新一年的挑战。如图是王师傅做的一块长方体的撑腰糕,前、后两个面是边长为4.5厘米的正方形,将其切成四块后表面积增加了440.5平方厘米。那么原长方体撑腰糕的体积是多少立方厘米
参考答案:
一、1.0.9 2.8 0.76 0.36 0.125 2.5 1
2.0 9702 40 9
3. ①③⑤⑥⑦⑧ 5×3×2+4×3×2+5×4×2=94(平方厘米)3×4×5=60(立方厘米)
二、1. < < = < 2.10 216
3.72 4.66 44 5.8 96
6.(1)6 16 (2)180
7.280 544 8.200 9.72
10.2.5
提示:先分别求出A、B部分水的体积,再求出水槽中水的总体积,最后求出隔板抽出后水槽的水高。B部分底面积为 10平方分米,水高为4分米,所以B部分水的体积为 10×4=40(立方分米),A部分底面积为15平方分米,水高为1.5分米,所以A部分水的体积为15×1.5=22.5(立方分米)。水槽中水的总体积为A部分水的体积加上 B部分水的体积,即40+22.5=62.5(立方分米),水槽的底面积为A部分和B部分底面积之和,即15+10=25(平方分米),所以隔板抽出后水槽的水高为62.5÷25=2.5(分米)。
三、1. C 2. C 3. B 4. C 5. B 6. B 7. A8. B 9. AC
四、1.一半 长方体的底面积×高÷2 三棱柱 高2. 1500 2000 1750
五、1. 32×2+25×4+20×6+28=312(厘米)
2. (1)80厘米=8分米 60厘米=6分米
150厘米=15分米 8×6×15=720(立方分米)
(2)40厘米=4分米
3. (1)12-1×2=10(分米) 8-1×2=6(分米)
5-1=4(分米)10×6×4=240(立方分米)=240升
(2)12×5×2+8×5×2+12×8×2+10×4×2+6×4×2=520(平方分米)
520×1.5=780(元)
4. 4分米=40厘米
12×8×20÷(40×40)+28=29.2(厘米)
5.答案不唯一,如:选乙、丁数据:
长、宽:24÷4=6(分米)
高:6-2=4(分米)
体积:6×6×4=144(立方分米)
6. (440.5-4.5×4.5×2)÷2×4.5=900(立方厘米)
