2.3.1等差数列的前n项和(第1课时)
文档属性
| 名称 | 2.3.1等差数列的前n项和(第1课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 346.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-09 14:21:08 | ||
图片预览






文档简介
课件19张PPT。§2.3.1
等差数列
的前n项和高中数学教师欧阳文丰制作复习数列的有关概念 如果数列 的第n项 与n之间的关系可以用一个公式来表示,这个公式就叫做这个数列的通项公式。数列 的前n项和等差数列 的通项公式为公式法 已知 求高 斯 的 故 事 高斯上小学时,有一次数学老 师给同学们出了一道 题:计算从1到100的自然数之和。那个老师认为,这些孩子算这道题目需要很长时间,所以他一写完题目,就坐到一边看书去了。谁知,他刚坐下,马上就有一个学生举手说:“老师,我做完了。”老师大吃一惊,原来是班上年纪最小的高斯。老师走到他身边,只见他在笔记本上写着5050,老师看了,不由得暗自称赞。为了鼓励他,老师买了一本数学书送给他。思考:现在如果要你算,你能否用简便的方法来算出它的值呢??问题引导,探究发现教学过程1+2+3+ … +98+99+10010150 ×(1+100)=5050高斯 Gauss.C.F
(1777~1855)
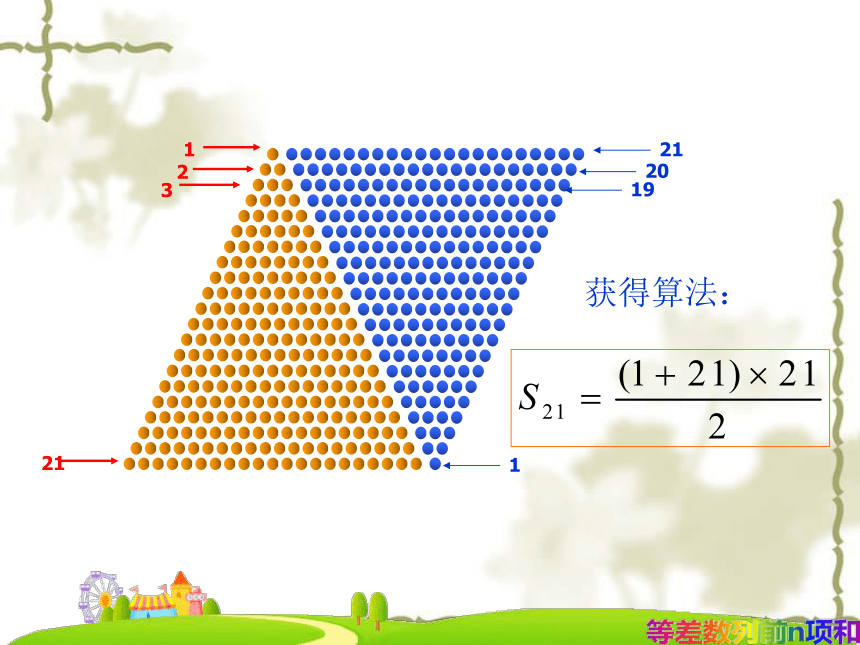
德国著名数学家1+100=2+99=3+98=???=50+51=101问题1:图案中,第1层到第21层一共有多少颗宝石?
这是求奇数个项的和的问题,能不能直接用高斯的办法呢求和呢?等差数列前n项和 问题1:图案中,第1层到第21层一共有多少颗宝石?等差数列前n项和获得算法:等差数列前n项和问题3:问题引导,探究发现教学过程方法1:方法2:+)2Sn=n(a1+an)+)2Sn=n(a1+an)此种求和法
称为
倒序相加法问题引导,探究发现问题4:若已知等差数列{an}的a1,d和n求Sn教学过程公式3公式与梯形面积:补成平形四边形分割成一个平行四边形和一个三角形 两个公式的共同已知量是a1和n,不同的已知量是:公式(1)已知an,公式(2)已知d 。 已知三个量就可以求出Sn ,我们要根据具体题目,灵活采用这两个公式。 (n-1)d求和公式的三种形式反思 反思:(1)“倒序相加求和”法
(2)两公式中涉及到a,an,Sn,n, d五个量,通常巳 知其中三个,就可以求出另外两个(知三求二),而且方法 就是解方程组,这是等差数列求和的基本问题。
(3)具体应用时还常结合等差数列的性质。 公式3[小问题·大思维]
1.数列{an}的前n项和Sn与通项an之间有什么关系?2.“等差数列的前n项和公式是关于n的二次函数”,这种
说法正确吗?
提示:不一定正确.当d≠0时,Sn=An2+Bn(A≠0)是关于n的二次函数;当d=0时,Sn=na1=a1n是关于n的一次函数.3.如何根据条件选择等差数列前n项和公式?当给出末项和公差时,利用例1:根据下列各题中的条件,求相应的等差数列{an}的Sn 例2、2000年11月14日教育部下发了《关于在中小学实施“校校通”工程的通知》.某市据此提出了实施“校校通”工程的总目标:从2001年起用10年的时间,在全市中小学建成不同标准的校园网。据测算,2001年该市用于“校校通”工程的经费为500万元。为了保证工程的顺利实施,计划每年投入的资金都比上一年增加50万元。那么从2001年起未来10年内,该市在“校校通”工程中的总投入是多少? 例3:已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?
分析:若要确定其前n项求和公式,则要确定a1和d,由已知条件可获两个关于a1和d的关系式,从而可求得.解:由题意知代入公式可得 解得小结:1.公式的推导方法:倒序相加法。3.公式的应用。2.等差数列前n项和公式。在公式中有 a1, an, n, d, sn五个量,
已知其中三个可以求出另外两个。教材P46A组2、5。布置作业:
(1777~1855)
德国著名数学家1+100=2+99=3+98=???=50+51=101问题1:图案中,第1层到第21层一共有多少颗宝石?
这是求奇数个项的和的问题,能不能直接用高斯的办法呢求和呢?等差数列前n项和 问题1:图案中,第1层到第21层一共有多少颗宝石?等差数列前n项和获得算法:等差数列前n项和问题3:问题引导,探究发现教学过程方法1:方法2:+)2Sn=n(a1+an)+)2Sn=n(a1+an)此种求和法
称为
倒序相加法问题引导,探究发现问题4:若已知等差数列{an}的a1,d和n求Sn教学过程公式3公式与梯形面积:补成平形四边形分割成一个平行四边形和一个三角形 两个公式的共同已知量是a1和n,不同的已知量是:公式(1)已知an,公式(2)已知d 。 已知三个量就可以求出Sn ,我们要根据具体题目,灵活采用这两个公式。 (n-1)d求和公式的三种形式反思 反思:(1)“倒序相加求和”法
(2)两公式中涉及到a,an,Sn,n, d五个量,通常巳 知其中三个,就可以求出另外两个(知三求二),而且方法 就是解方程组,这是等差数列求和的基本问题。
(3)具体应用时还常结合等差数列的性质。 公式3[小问题·大思维]
1.数列{an}的前n项和Sn与通项an之间有什么关系?2.“等差数列的前n项和公式是关于n的二次函数”,这种
说法正确吗?
提示:不一定正确.当d≠0时,Sn=An2+Bn(A≠0)是关于n的二次函数;当d=0时,Sn=na1=a1n是关于n的一次函数.3.如何根据条件选择等差数列前n项和公式?当给出末项和公差时,利用例1:根据下列各题中的条件,求相应的等差数列{an}的Sn 例2、2000年11月14日教育部下发了《关于在中小学实施“校校通”工程的通知》.某市据此提出了实施“校校通”工程的总目标:从2001年起用10年的时间,在全市中小学建成不同标准的校园网。据测算,2001年该市用于“校校通”工程的经费为500万元。为了保证工程的顺利实施,计划每年投入的资金都比上一年增加50万元。那么从2001年起未来10年内,该市在“校校通”工程中的总投入是多少? 例3:已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?
分析:若要确定其前n项求和公式,则要确定a1和d,由已知条件可获两个关于a1和d的关系式,从而可求得.解:由题意知代入公式可得 解得小结:1.公式的推导方法:倒序相加法。3.公式的应用。2.等差数列前n项和公式。在公式中有 a1, an, n, d, sn五个量,
已知其中三个可以求出另外两个。教材P46A组2、5。布置作业:
