2.3.2等差数列的前n项和(第2课时)
文档属性
| 名称 | 2.3.2等差数列的前n项和(第2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 337.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-04 20:06:34 | ||
图片预览








文档简介
课件23张PPT。2.3等差数列的前n项和(第2课时)高中数学教师欧阳文丰制作复习回顾1.等差数列前n项和Sn公式的推导
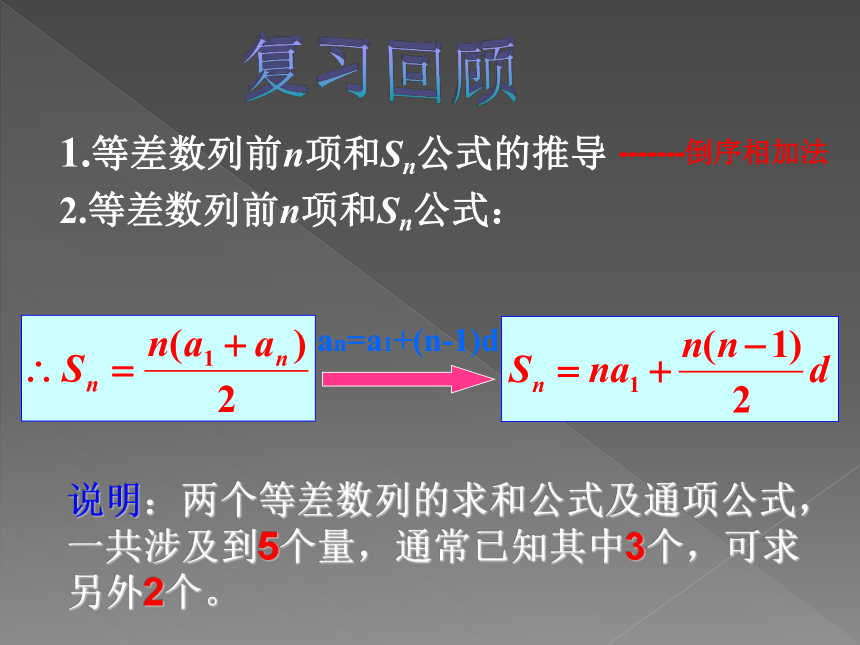
2.等差数列前n项和Sn公式:an=a1+(n-1)d说明:两个等差数列的求和公式及通项公式,一共涉及到5个量,通常已知其中3个,可求另外2个。-------倒序相加法 一般地,如果一个数列{an} 的前n项和为
其中p、q、r为常数,且p?0,那么这个数列一定是等差数列吗?如果是,它的首项与公差是什么?探究等差数列前n项和公式:Sn=n(a1+an)/2 (1)
Sn=na1+n(n-1)d/2 (2)对于公式(2)可整理为
Sn=(n2d/2)+[ a1-(d/2)]n
这说明Sn是关于n的一元二次函数。1.等差数列的前n项和公式:小结2. 若{an}成等差数列,则{ }也成等差数列故只有当r=0时该数列才是等差数列,
此时首项a1=p+q,公差d=2p(p≠0)例1. 已知数列{an}的前n项和为 ,求该
数列的通项公式,这个数列是等差数列吗?如果是,
它的首项和公差分别是什么?三、例题解:∵Sn=a1+a2+…+an,Sn-1=a1+a2+…+an-1(n>1)当n=1时,①∴ a1也满足①式 ∴当n>1时,所以数列{an}的通项公式为:由此可知,数列{an}是一个首项为1.5,公差为2的
等差数列例3 已知等差数列{an}中,a1=-2,并且S3=S7,试求Sn的最小值及此时的n的值。 解:设该等差数列的公差为d。由S3=S7得
3×(-2)+(3×2/2)×d=7×(-2)+(7×6/2) ×d,得d=4/9。Sn=-2n+[n(n-1)/2]×4/9
=2/9×n2-20/9n
=2/9(n2-10n)
=2/9(n-5)2-50/9
所以n=5时前n项和最小,最小值为-50/9。
解法二:设该等差数列的公差为d。由S3=S7得
3×(-2)+(3×2/2)×d=7×(-2)+(7×6/2) ×d,得d=4/9。
所以通项公式an=-2+(n-1)×4/9
由首项及公差知:该数列为递增等差数列。
由方程an=0得 -2+(n-1)4/9=0
解得n=5.5 取 n=5根据数列递增性可知a1,a2, a3,a4,a5均为负数,从第六项起以后各项均为正数,因此前五项的和最小。代入求和公式Sn=5×(-2)+[5×(5-1)/2]×4/9=-50/9
解法三:设该等差数列的公差为d。由S3=S7得
3×(-2)+(3×2/2)×d=7×(-2)+(7×6/2) ×d,得d=4/9。
由首项及公差知:该数列为递增等差数列。 等差数列前n项和Sn 是n的二次函数,而S3=S7
正说明二次函数是以n=(3+7)/2为对称轴,
且二次函数开口向上,所以当n =5时Sn有最小值。
将n =5 代入前n项和公式,有
Sn=5×(-2)+[5×(5-1)/2]×4/9=-50/9
解法四:设该等差数列的公差为d。由S3=S7得
3×(-2)+(3×2/2)×d=7×(-2)+(7×6/2) ×d,得d=4/9。所以通项公式an=-2+(n-1)×4/9
由首项及公差知:该数列为递增等差数列。 解得 4.5≤n ≤5 .5 所以n=5 即前5项的和最小,将
n =5 代入前n项和公式,
有Sn=5×(-2)+[5×(5-1)/2]×4/9=-50/9
小结:等差数列前n项和最值的求法有 注:(1)当数列是首项为正,公差为负的递减等 差数列时,才有前n项和最大。
(2)当数列是首项为负,公差为正的递增等差数列时,前n项和才有最小值。 (1)函数最值法 (解法一)
(2)解方程法 (解法二)
(3)对称轴法 (解法三)
(4)不等式法 (解法四)
作业:
1 一个首项为a(a>0)的等差数列,前3项和
与前10项和相等,问此数列的前几项和
最大,并求出最大值。
2 设等差数列{an}的前n项和Sn,已知 a13=-12,
S12>0,S13<0
(1) 求公差d的取值范围
(2) 指出S1,S2……S12中哪一个值最大,并
说出理由1 解:由a1+a2=91,a2+a3=85可得
4a2=176,则a2=44,所以a1=47,
d=-3.
接下来即可用求最值的方法 求得前16项的和最大,最大值为392。 拼搏 2 解:由a1=31,d=-4可的此数 列的通项公式an=35-4n.
当n=8时, an=3;
当n=9时, an=-1;
所以与零最靠近的项是 a9.进取或由an=35-4n=0,得n=35/4,
当n =9时, an 与零最接近。练:已知数列{an}的前n项和公式为Sn=2n2-30n
(1)这个数列是等差数列吗?求出它的通项公式;
(2)求使得Sn最小的序号n的值。解:(1)将n-1代入到数列的前n项和公式,
得Sn-1=2(n-1)2-30(n-1),因此an=Sn-Sn-1=4n-32,(n≥2),当n=1时,a1=S1=2-30=-28,也适合上式,
所以这个数列的通项公式是an=4n-32。(2)因为 又因为n是正整数,
所以当n=7或=8时,Sn最小,
最小值是-112.1. 若数列的前n项和为 则数列( )(A)是公差为2的等差数列
(B)是公差为5的等差数列
(C)是公差为10的等差数列
(D)是公差为-10的等差数列C练习:2.在等差数列{an}中,a2+a4=p,a3+a5=q.则其前6项的和S6为( )
(A) 5 (p+q)/4 (B) 3(p+q)/2 (C) p+q (D) 2(p+q)B3. 已知等差数列{an}的前n项和为Sn,
若a4=18- a5,则S8等于( )
A.18 B.36 C.54 D.72 D
2.等差数列前n项和Sn公式:an=a1+(n-1)d说明:两个等差数列的求和公式及通项公式,一共涉及到5个量,通常已知其中3个,可求另外2个。-------倒序相加法 一般地,如果一个数列{an} 的前n项和为
其中p、q、r为常数,且p?0,那么这个数列一定是等差数列吗?如果是,它的首项与公差是什么?探究等差数列前n项和公式:Sn=n(a1+an)/2 (1)
Sn=na1+n(n-1)d/2 (2)对于公式(2)可整理为
Sn=(n2d/2)+[ a1-(d/2)]n
这说明Sn是关于n的一元二次函数。1.等差数列的前n项和公式:小结2. 若{an}成等差数列,则{ }也成等差数列故只有当r=0时该数列才是等差数列,
此时首项a1=p+q,公差d=2p(p≠0)例1. 已知数列{an}的前n项和为 ,求该
数列的通项公式,这个数列是等差数列吗?如果是,
它的首项和公差分别是什么?三、例题解:∵Sn=a1+a2+…+an,Sn-1=a1+a2+…+an-1(n>1)当n=1时,①∴ a1也满足①式 ∴当n>1时,所以数列{an}的通项公式为:由此可知,数列{an}是一个首项为1.5,公差为2的
等差数列例3 已知等差数列{an}中,a1=-2,并且S3=S7,试求Sn的最小值及此时的n的值。 解:设该等差数列的公差为d。由S3=S7得
3×(-2)+(3×2/2)×d=7×(-2)+(7×6/2) ×d,得d=4/9。Sn=-2n+[n(n-1)/2]×4/9
=2/9×n2-20/9n
=2/9(n2-10n)
=2/9(n-5)2-50/9
所以n=5时前n项和最小,最小值为-50/9。
解法二:设该等差数列的公差为d。由S3=S7得
3×(-2)+(3×2/2)×d=7×(-2)+(7×6/2) ×d,得d=4/9。
所以通项公式an=-2+(n-1)×4/9
由首项及公差知:该数列为递增等差数列。
由方程an=0得 -2+(n-1)4/9=0
解得n=5.5 取 n=5根据数列递增性可知a1,a2, a3,a4,a5均为负数,从第六项起以后各项均为正数,因此前五项的和最小。代入求和公式Sn=5×(-2)+[5×(5-1)/2]×4/9=-50/9
解法三:设该等差数列的公差为d。由S3=S7得
3×(-2)+(3×2/2)×d=7×(-2)+(7×6/2) ×d,得d=4/9。
由首项及公差知:该数列为递增等差数列。 等差数列前n项和Sn 是n的二次函数,而S3=S7
正说明二次函数是以n=(3+7)/2为对称轴,
且二次函数开口向上,所以当n =5时Sn有最小值。
将n =5 代入前n项和公式,有
Sn=5×(-2)+[5×(5-1)/2]×4/9=-50/9
解法四:设该等差数列的公差为d。由S3=S7得
3×(-2)+(3×2/2)×d=7×(-2)+(7×6/2) ×d,得d=4/9。所以通项公式an=-2+(n-1)×4/9
由首项及公差知:该数列为递增等差数列。 解得 4.5≤n ≤5 .5 所以n=5 即前5项的和最小,将
n =5 代入前n项和公式,
有Sn=5×(-2)+[5×(5-1)/2]×4/9=-50/9
小结:等差数列前n项和最值的求法有 注:(1)当数列是首项为正,公差为负的递减等 差数列时,才有前n项和最大。
(2)当数列是首项为负,公差为正的递增等差数列时,前n项和才有最小值。 (1)函数最值法 (解法一)
(2)解方程法 (解法二)
(3)对称轴法 (解法三)
(4)不等式法 (解法四)
作业:
1 一个首项为a(a>0)的等差数列,前3项和
与前10项和相等,问此数列的前几项和
最大,并求出最大值。
2 设等差数列{an}的前n项和Sn,已知 a13=-12,
S12>0,S13<0
(1) 求公差d的取值范围
(2) 指出S1,S2……S12中哪一个值最大,并
说出理由1 解:由a1+a2=91,a2+a3=85可得
4a2=176,则a2=44,所以a1=47,
d=-3.
接下来即可用求最值的方法 求得前16项的和最大,最大值为392。 拼搏 2 解:由a1=31,d=-4可的此数 列的通项公式an=35-4n.
当n=8时, an=3;
当n=9时, an=-1;
所以与零最靠近的项是 a9.进取或由an=35-4n=0,得n=35/4,
当n =9时, an 与零最接近。练:已知数列{an}的前n项和公式为Sn=2n2-30n
(1)这个数列是等差数列吗?求出它的通项公式;
(2)求使得Sn最小的序号n的值。解:(1)将n-1代入到数列的前n项和公式,
得Sn-1=2(n-1)2-30(n-1),因此an=Sn-Sn-1=4n-32,(n≥2),当n=1时,a1=S1=2-30=-28,也适合上式,
所以这个数列的通项公式是an=4n-32。(2)因为 又因为n是正整数,
所以当n=7或=8时,Sn最小,
最小值是-112.1. 若数列的前n项和为 则数列( )(A)是公差为2的等差数列
(B)是公差为5的等差数列
(C)是公差为10的等差数列
(D)是公差为-10的等差数列C练习:2.在等差数列{an}中,a2+a4=p,a3+a5=q.则其前6项的和S6为( )
(A) 5 (p+q)/4 (B) 3(p+q)/2 (C) p+q (D) 2(p+q)B3. 已知等差数列{an}的前n项和为Sn,
若a4=18- a5,则S8等于( )
A.18 B.36 C.54 D.72 D
