第5章 力与平衡 章末整合课件 (1)

课件25张PPT。章 末 整 合网络建构力与平衡力的合成与分解
共点力作用下物体的平衡
力的合成
与分解共
点
力
作
用
下
物
体
的
平
衡专题讲座连接体的平衡问题解决共点力的平衡问题，关键是对研究对象进行准确的受力分析，受力分析时应注意不同力产生的条件及方向特点，然后根据共点力的平衡条件在所选的方向上列平衡方程，再分析、求解．
连接体是多个相互关联的物体组成的物体组(或物体系)，分析连接体问题时，常用整体法和隔离法来进行受力分析．由于对于连接体问题，多数情况即要分析外力，又要分析内力，这时我们可以采取先整体(解决外力)后隔离(解决内力)的方法，当然个别情况也可运用先隔离再整体的相反顺序．
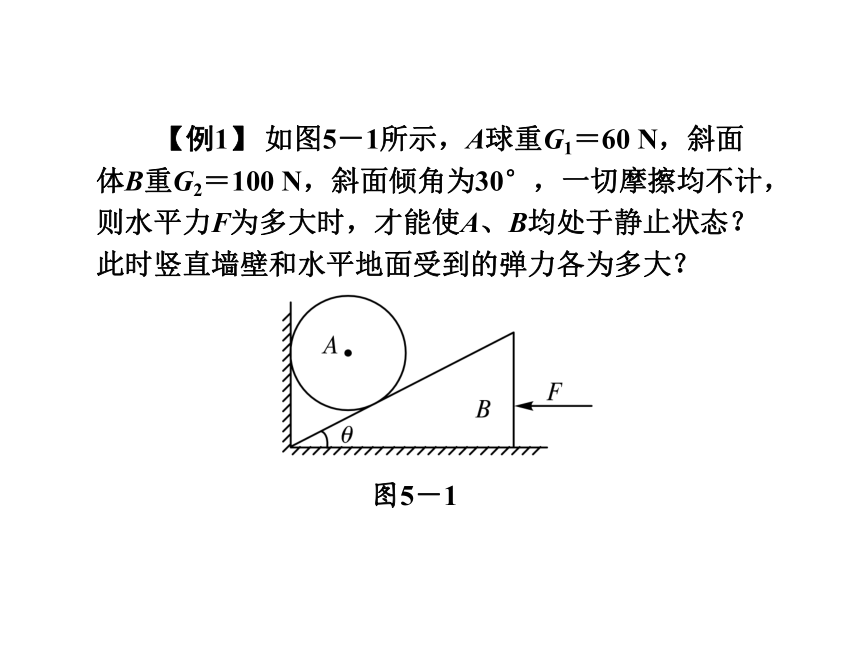
【例1】 如图5－1所示，A球重G1＝60 N，斜面体B重G2＝100 N，斜面倾角为30°，一切摩擦均不计，则水平力F为多大时，才能使A、B均处于静止状态？此时竖直墙壁和水平地面受到的弹力各为多大？
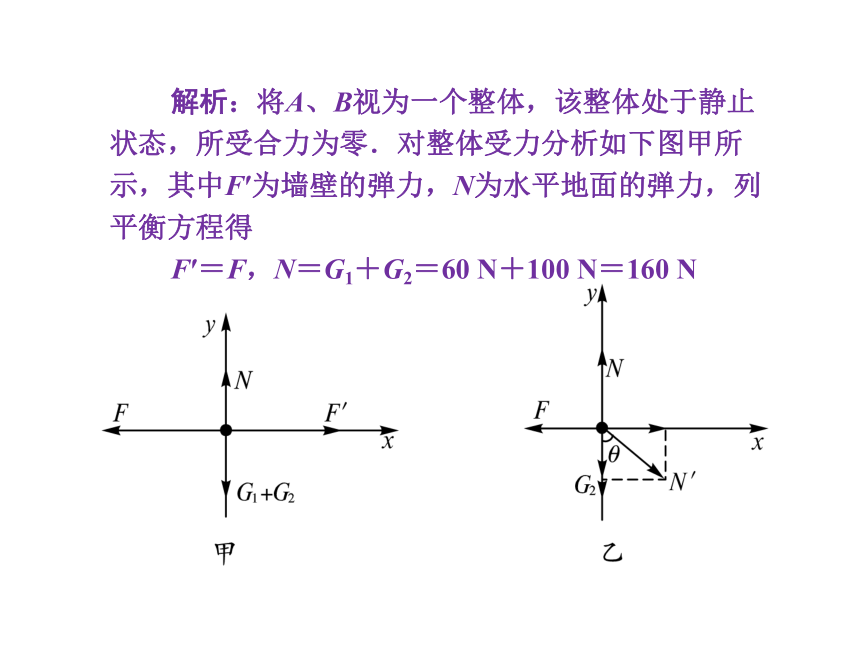
图5－1解析：将A、B视为一个整体，该整体处于静止状态，所受合力为零．对整体受力分析如下图甲所示，其中F′为墙壁的弹力，N为水平地面的弹力，列平衡方程得
F′＝F，N＝G1＋G2＝60 N＋100 N＝160 N
隔离斜面体B，进行受力分析如图乙所示，其中N′为球A对斜面体的压力，将压力N′正交分解后，列平衡方程为F＝N′sinθ，N＝N′cosθ＋G2
反思领悟：整体法与隔离法是很常用的分析力学问题的方法，但这两种方法并非孤立，很多具体问题，将整体法和隔离法结合起来应用分析，解题将更简便．
平衡状态下的临界与极值问题1．临界问题
平衡物体的临界状态是指物体所处平衡状态将要发生变化的状态，涉及临界状态的问题叫临界问题．也就是说在临界状态下，当某物理量发生变化时，会引起其他几个物理量的变化．
解决这类问题一定要注意“恰好出现”或“恰好不出现”的条件，基本方法是假设推理法，即先假设某种情况成立，然后再根据平衡条件及有关知识进行论证、求解．
2．极值问题
平衡物体的极值，一般指在力的变化过程中的最大值和最小值问题．研究平衡物体的极值问题有两种常用方法：
(1)解析法，即根据物体的平衡条件列出方程，在解方程时，采用数学知识求极值或者根据物理临界条件求极值．
(2)图解法，即根据物体的平衡条件作出力的矢量图，画出平行四边形或者矢量三角形进行动态分析，确定最大值或最小值．
【例2】 物体的质量为2 kg.两根轻细绳AB和AC的一端连接于竖直墙上，另一端A系于物体上，在物体上另施加一个方向与水平线成θ＝60°角的拉力F，如图5－2所示(图中物体当做质点)，若要使两绳都能伸直，求拉力F的大小范围．(g取10 N/kg)
图5－2解析：作出物体A的受力分析图，如下图所示，
由平衡条件可得，
Fsinθ＋F1sinθ＝mg
Fcosθ＝F2＋F1cosθ
反思领悟：运用假设法解决临界问题的基本步骤是：①明确研究对象，②画受力图，③假设可发生的临界现象，④列出满足所发生的临界现象的平衡方程求解．
易错分析由于方法不当导致受力分析错误【典例1】 如图5－3所示，物体A靠在竖直墙面上，在力F的作用下，物体A、B保持静止．物体A的受力个数为 (　　)
?
A．2 B．3 C．4 D．5
图5－3错因分析：以A为研究对象，A受到重力、B对它的斜向上的弹力、B对它的斜向上的摩擦力和墙壁对它向右的弹力四个力的作用，选C.
解析：先以A、B整体为研究对象，整体受到向上的推力F和重力(墙壁对A无弹力)；再以A为研究对象，A受到竖直向下的重力、B对它的支持力和摩擦力，所以A受到三个力的作用，选项B正确．
答案：B
纠错心得：对物体进行受力分析时不能想当然，要善于变换研究对象，运用联系的观点，灵活应用整体法和隔离法．
力的相互作用中矢量三角形应用不当?【典例2】 如图5－4所示，质量均可忽略的轻绳与轻杆承受弹力的最大值一定，轻杆A端用铰链固定，滑轮在A点正上方(滑轮大小及摩擦均可不计)，B端吊一重物，重力大小为G.现将绳的一端拴在杆的B端，用拉力F将B端缓慢上拉(均未断)，在AB杆达到竖直前，以下分析正确的是 (　　)
图5－4A．绳子越来越容易断
B．绳子越来越不容易断
C．AB杆越来越容易断
D．AB杆越来越不容易断
错解剖析：错解1：认识不到B点的受力特点，认为用拉力F将B端缓慢上拉的过程中，B点受重物的拉力一定，但随着绳子OB越来越短，绳子的拉力会越来越大，所以选择A；错解2：认识不到B点的受力特点，认为用拉力F将B端缓慢上拉的过程中，B点受重物的拉力一定，但AB杆越接近竖直其承受的力越大，所以选择C.
解析：以B点为研究对象，进行受力分析．B点受重物的拉力一定，大小为G，轻绳的拉力F，沿轻杆方向倾斜向上的支持力N.由于是缓慢拉动，所以B点处于动态平衡状态，F和N的合力即为重物拉力的平衡力．根据三个力的特点，在B点可得矢量三角形如右图答案：B纠错心得：处理动态平衡问题的方法，就是在原来处理平衡问题的基础上，注意分析由于某一个物理量的变化，而带来的其他变化，这里经常用到图解法，虽然也可以用数学函数讨论法，但矢量三角形往往会带来意想不到的简捷，审题时注意分析每个力的特点，包括大小和方向，分清不变量和变量的变化特点，仔细寻找三角形的特殊关系．
?