2025-2026学年苏教版六年级上册数学第一单元长方体和正方体高频填空题(含解析)
文档属性
| 名称 | 2025-2026学年苏教版六年级上册数学第一单元长方体和正方体高频填空题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 566.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-29 00:00:00 | ||
图片预览




文档简介
2025-2026学年苏教版六年级上册数学第一单元长方体和正方体高频填空题
1.在括号里填上合适的单位。
一台家用冰箱的容积大约是450( ) 一个游泳池可装水2500( )
教室的面积约是80( ) 40.4立方米=( )立方分米
6500毫升=( )立方厘米=( )立方分米
2.一个杯子最多能装250mL,是指杯子的( )是250mL。
3.一个正方体相对两个面上的数互为倒数,如图是它的展开图,A面上的数是( ),抛起这个正方体,落下后整数朝上的可能性比分数朝上的可能性( )。(填“大”“小”或“相等”)
4.一个长4分米,宽2分米,高4分米的长方体,它的占地面积最大是( ),它的表面积是( )。
5.一个正方体的棱长是4分米,它的表面积是( )。
6.正方体有( )个面,( )条棱,( )个顶点,从不同的角度最多能看到( )个面。
7.长方体有( )个顶点,( )条棱,包含( )组相对的棱,( )组相对的面,相对的面( ),相交于同一个顶点的三条棱的长度分别叫作长方体的( )、( )、( )。
8.把一根长3.5dm的长方体木料截成6段(如图),表面积比原来增加了,这根木料原来的体积是( )。
9.一个正方体的棱长是5厘米,它的体积是( )立方厘米。
10.一个棱长是4dm的正方体水箱中装有半箱水。把一块铁块完全浸入水中,水面上升了6cm,这个铁块的体积是( )。
11.一个长方体的玻璃鱼缸,长60厘米,宽5分米,高4分米,这个玻璃鱼缸的体积是( )。
12.一个横截面是正方形的长方体通风管长36cm,其侧面展开后恰好是一个正方形(如图),这个通风管的宽和高都是( )cm,制作这个通风管需要( )的材料。
13.一个长方体是由三个同样大小的正方体拼成的,如果去掉最右边的一个正方体,表面积就比原来减少30cm2,原来长方体的表面积是( )cm2。
14.在一个底面积72平方厘米、高10厘米的长方体容器中,水深2厘米。如果放入一个棱长6厘米的正方体铁块,这时水深( )厘米。
15.一个长方体,其中两个相对的面为边长10厘米的正方形,这个长方体的表面积是1000平方厘米,它的体积是( )立方厘米。
16.一个长方体长10厘米,宽8厘米,高5厘米,表面积是( )平方厘米,体积是( )立方厘米。
17.把3个棱长2分米的正方体拼成一个长方体,长方体的表面积是( )平方分米,体积是( )立方分米。
18.一个长方体木箱,底面周长是3米,高5分米,表面积是258平方分米。这个木箱的底面积是( )平方分米。
19.把两个棱长8厘米的正方体拼成一个长方体后,表面积减少( )平方厘米。
20.把一个表面积是72平方分米的正方体木块放在桌面上,木块在桌面上所占的面积是( )平方分米。
21.用一根长144厘米的铁丝围成一个正方体框架,棱长是( )厘米;如果用它围成一个长方体框架,长是20厘米,宽是10厘米,那么高是( )厘米。
22.一个正方体铁皮油箱的棱长为2.5分米,如果里面的油深2分米,这个油箱里有油( )升。
23.下图是一个长方体的表面展开图,这个长方体的表面积是( ),体积是( )。
24.一个长方体长25厘米,宽16厘米,高9厘米,它的占地面积最大是( )平方厘米,最小是( )平方厘米,体积是( )立方厘米。
25.用一根铁丝正好能做成一个长6分米、宽4分米、高2分米的长方体框架,这根铁丝长( )分米;如果改做成一个正方体框架,棱长是( )分米。
26.12盒磁带按“规则方式”打包,所谓“规则方式”是指每相邻两盒必须是以全等的面积对接,最后得到的包装形状是一个长方体。已知磁带盒的长为11厘米,宽为7厘米,高为2厘米。按“规则方式”打包得到的长方体的表面积的最小值是( )平方厘米。
27.如图是一个正方体的展开图,六个面上分别写有这六个数字,相对的两个面上数字的和最大是( ),相对的两个面上数字的差最小是( )。
28.一个正方体木块六个面上分别写上小、南、狮、爱、生、活这六个汉字。从不同角度看这个正方体,如图所示,通过推断可知“南”的对面是( )。
29.一个底面是正方形的长方体盒子,侧面展开图是一个边长为8厘米的正方形,这个长方体的侧面积是( )平方厘米,体积是( )立方厘米。
30.一张长方形铁皮(如图),长是20厘米,宽是( )厘米。用图中的阴影部分向里折成一个正方体盒子,盒子的体积是( )立方厘米。和D面相对的是( )面;如果D面是底面,从前面看是C面,那么右面是( )面。
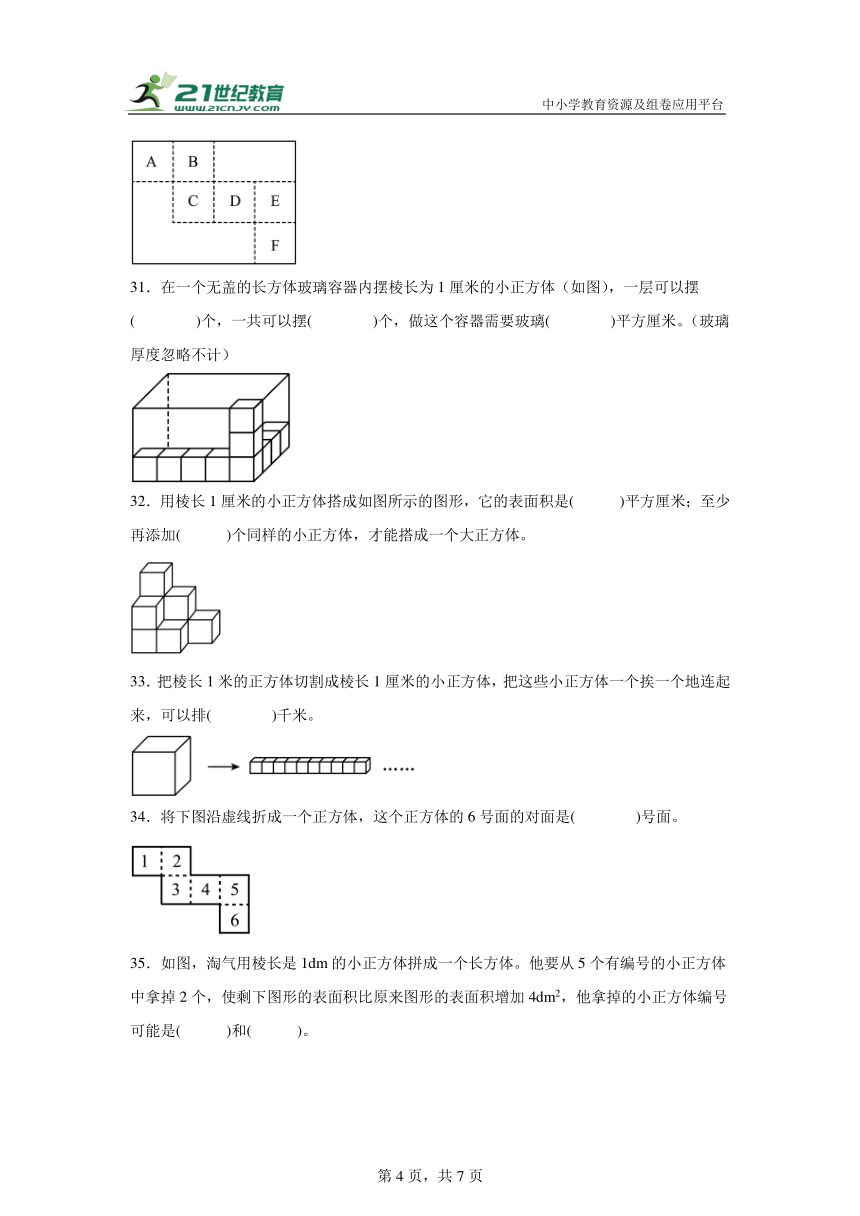
31.在一个无盖的长方体玻璃容器内摆棱长为1厘米的小正方体(如图),一层可以摆( )个,一共可以摆( )个,做这个容器需要玻璃( )平方厘米。(玻璃厚度忽略不计)
32.用棱长1厘米的小正方体搭成如图所示的图形,它的表面积是( )平方厘米;至少再添加( )个同样的小正方体,才能搭成一个大正方体。
33.把棱长1米的正方体切割成棱长1厘米的小正方体,把这些小正方体一个挨一个地连起来,可以排( )千米。
34.将下图沿虚线折成一个正方体,这个正方体的6号面的对面是( )号面。
35.如图,淘气用棱长是1dm的小正方体拼成一个长方体。他要从5个有编号的小正方体中拿掉2个,使剩下图形的表面积比原来图形的表面积增加4dm2,他拿掉的小正方体编号可能是( )和( )。
36.把一个长、宽、高分别为6厘米、5厘米、4厘米的长方体切成两个完全相同的长方体,表面积最多可以增加( )平方厘米,最少可以增加( )平方厘米。
37.把2个棱长4分米的正方体拼成一个长方体(如图),拼成的长方体的表面积是( )平方分米。
38.将一个棱长是10厘米的正方体容器装满水,再把水全部倒入长20厘米,宽10厘米的长方体容器。此时长方体容器水深( )厘米。
39.如图,王师傅把长的长方体木料锯成3个相同的小长方体,表面积增加了,原来长方体木料的体积是( )。
40.一个长方体长8分米,宽5分米,高3分米,它的表面积是( )平方分米。如果高减少2分米,表面积减少( )平方分米。
41.把一根长3米的长方体木料沿与长垂直的截面锯成两段,锯开后两段木料的表面积之和比原来木料的表面积增加了40平方厘米。这根木料的体积是( )立方米。
42.把一个表面积是55.5平方厘米的长方体,沿着长、宽、高垂直各切一刀后分成了8个小长方体(如图),表面积比原来增加了( )平方厘米。
43.12个棱长的正方体,如图继续拼下去,拼成的新长方体,表面积减少了( )。
44.有小中大三个正方体水池,从里面测量它们的边长分别是2米、3米、6米,把两堆沙分别倒入小、中号水池,水面分别上升了4厘米、6厘米,如果把两堆沙都倒入大号水池,大号水池水面上升( )厘米。
45.用棱长为1厘米的小正方体拼成下面的图形,这个图形的表面积是( )平方厘米,体积是( )立方厘米。
46.如图是用棱长1厘米的正方体木块摆成的几何体,它的体积是( )立方厘米,表面积是( )平方厘米。
47.一个包装箱长4分米、宽2分米、高2.5分米,王师傅用胶带缠绕进行打包(如图所示),至少需要胶带 分米;做这个包装箱至少需要硬纸板 平方分米。
48.把长1.5米的长方体材料(如图),平均锯成3段,表面积比原来增加2.4平方分米,原来这根木料的体积是 立方分米。
49.如图1是边长为30厘米的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体纸盒。已知该长方体的宽是高的2倍,则它的表面积是( )平方厘米,体积是( )立方厘米。
50.用铁丝围成一个长方体框架,长10厘米,宽8厘米,高6厘米,铁丝长( )厘米;如果给它各个面蒙上彩纸,至少要( )平方分米的彩纸;这个长方体所占的空间是( )立方厘米。
51.底面是正方形的长方体,侧面展开是周长16分米的正方形,它的表面积是( )平方分米。
52.把一根 2.5米长的长方体木料垂直于长锯成4段,表面积增加48平方分米。原来这根木料的体积是( )立方分米。
53.一个长方体,如果高增加3厘米,就变成一个正方体。这时表面积比原来增加了96平方厘米。原来长方体的高是( )厘米。
54.一个正方体的体积是64立方分米,它的底面积是( )平方分米。
55.一个无盖的长方体玻璃鱼缸,长和宽都是5分米,高4分米,在里面倒入高3分米的水,与水接触的玻璃的面积是( )平方分米。
56.做一节长1.2米,宽和高都是10厘米的通风管,至少需要铁皮( )平方厘米。
57.一个棱长是2米的无盖正方体蓄水箱,它的占地面积是( )平方米,制作一个至少需要( )平方米铁皮。
58.如图,一个长方体的长、宽、高分别是a米、b米、h米。如果高增加2米,体积比原来增加( )立方米。
59.把棱长1m的正方体木块切成棱长1cm的小正方体木块,一共能切( )块,把它们排成一排,排成的距离比1km多( )km。
60.如下图,在一块平坦的地面上,实践社团的同学们在工人师傅的帮助下,用砖围了一个长方体水池,池壁厚10(底面利用原有的水泥地)。这个水池的容积是( )。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第2页,共7页
第7页,共7页
《2025-2026学年苏教版六年级上册数学第一单元长方体和正方体高频填空题》参考答案
1. 升/L 立方米/m3 平方米/m2 40400 6500 6.5
【分析】容积单位有升(L)、毫升(mL),家用冰箱容积较大,用升作单位合适。比如常见的小型家用双门冰箱容积大概300~500升。
游泳池装水量很大,体积单位用立方米(m3)合适。比如一个小型游泳池一般能装水几千立方米,2500立方米符合小型游泳池的规模。
面积单位有平方米(m2)、平方分米等,教室面积用平方米衡量合适。比如一间卧室的面积是60平方米。
1立方米=1000立方分米,大单位换小单位乘进率。
1毫升=1立方厘米,所以6500毫升=(6500)立方厘米。1立方分米=1000立方厘米,小单位换大单位除以进率。
【详解】家用冰箱容积较大,用升作单位合适。一台家用冰箱的容积大约是450升(L)。
游泳池装水量很大,用立方米作单位合适。一个游泳池可装水2500立方米(m3)。
教室面积用平方米衡量合适。教室的面积约是80平方米(m2)。
1立方米=1000立方分米
40.4×1000=40400(立方分米)
40.4立方米=40400立方分米
1毫升=1立方厘米
6500毫升=6500立方厘米
1立方分米=1000立方厘米
6500÷1000=6.5(立方分米)
6500毫升=6500立方厘米=6.5立方分米
2.容积
【分析】杯子的“最多能装250mL”指的是它内部所能容纳液体的最大体积,根据数学定义,容器能容纳物体的体积称为“容积”。
【详解】题目中描述杯子“最多能装250mL”,这里的“装”指杯子内部可以容纳的液体量。容器所能容纳物体的体积称为容积。
所以,一个杯子最多能装250mL,是指杯子的容积是250mL。
3. 大
【分析】观察展开图,折成正方体后,A面与3面相对(通过空间想象,把展开图还原成正方体,可确定3和A是对面)。然后根据倒数的定义确定具体的数。
可能性大小与数量多少有关,数量越多,朝上的可能性越大;先确定整数面和分数面的数量。相对面情况:3和A()相对、2和B相对、1和C相对。因为2的倒数是,所以B=;1的倒数是1,所以C=1。那么6个面的数分别是3(整数)、(分数)、2(整数)、(分数)、1(整数)、1(整数)。统计整数面和分数面数量:整数面有3、2、1、1,共4个;分数面有、,共2个。然后比较大小即可解答。
【详解】
所以A面上的数是。
整数面有3、2、1、1,共4个;分数面有、,共2个。
4>2
A面上的数是,抛起这个正方体,落下后整数朝上的可能性比分数朝上的可能性大。
4. 16平方分米 64平方分米
【分析】求它占地面积就是求的底面积,当以长4分米、高4分米为底面时的占地面积最大,根据长方形的面积=长×宽,长方体的表面积=(长×宽+宽×高+长×高)×2解答。
【详解】4×4=16(平方分米)
(4×2+2×4+4×4)×2
=(8+8+16)×2
=(16+16)×2
=32×2
=64(平方分米)
所以占地面积最大是16平方分米,表面积是64平方分米。
5.96平方分米/96dm2
【分析】根据正方体的表面积=棱长×棱长×6,代入数据计算即可。
【详解】4×4×6
=16×6
=96(平方分米)
所以表面积是96平方分米。
6. 6 12 8 3
【分析】正方体特征:有6个面都是正方形,且面积相等;有8个顶点;有12条棱且长度都相等。从不同的角度看正方体,最少能看到1个面,最多能看到3个面。据此解答。
【详解】正方体有6个面,12条棱,8个顶点,从不同的角度最多能看到3个面。
7. 8 12 3 3 完全相同 长 宽 高
【详解】长方体有8个顶点,12条棱,包含3组相对的棱,3组相对的面,相对的面完全相同,相交于同一个顶点的三条棱的长度分别叫作长方体的长、宽、高。
8.87.5dm3/87.5立方分米
【分析】把长方体木料截成6段,需要截的次数为6-1=5次。每截1次会增加2个截面的面积,那么截5次增加的截面数量是5×2=10个。已知表面积比原来增加了250dm2,增加的面积就是10个截面的面积之和,而每个截面的面积都等于长方体木料的底面积,所以木料的底面积为250÷10=25dm2。根据长方体体积公式V=Sh(其中V表示体积,S表示底面积,h表示高),已知木料长3.5dm,也就是高h=3.5dm,底面积S=25dm2,把数据代入公式计算即可。
【详解】6-1=5(次)
5×2=10(个)
250÷10=25(dm2)
25×3.5=87.5(dm3)
这根木料原来的体积是87.5dm3或87.5立方分米。
9.125
【分析】正方体的体积公式为V=a3(V代表体积,a为棱长),已知正方体的棱长是5厘米,把数据代入公式即可解答。
【详解】53
=5×5×5
=125(立方厘米)
它的体积是125立方厘米。
10.9.6
【分析】当把铁块完全浸入水中时,水面上升,上升的这部分水的形状为长方体,而铁块的体积就等于上升的这部分水的体积。已知正方体水箱棱长是4dm,水面上升了6cm,1dm=10cm,可得6cm为6÷10=0.6dm。上升的水的形状为长方体,该长方体的长和宽就是正方体水箱的棱长4dm,高为水面上升的高度0.6dm。根据长方体体积公式V=a×b×h(其中V表示体积,a表示长,b表示宽,h表示高),把数据代入公式可得上升的水的体积(即铁块体积)。
【详解】1dm=10cm
6÷10=0.6(dm)
4×4×0.6=9.6(dm3)
所以这个铁块的体积是9.6dm3。
11.120立方分米
【分析】长方体体积的计算公式为V=a×b×h(其中V表示体积,a表示长方体的长,b表示长方体的宽,h表示长方体的高)。已知玻璃鱼缸长60厘米,宽5分米,高4分米,1分米=10厘米,可得60厘米为60÷10=6分米。然后把数据代入公式计算即可解答。
【详解】1分米=10厘米
60÷10=6(分米)
6×5×4=120(立方分米)
这个玻璃鱼缸的体积是120立方分米(dm3)或120000立方厘米(cm3)。
12. 9 1296
【分析】(1)由题意知,通风管的横截面是正方形,侧面展开后恰好是一个正方形,通风管长36cm,即侧面展开图正方形的边长为36cm,而侧面展开图的边长也等于底面正方形的周长,即可求出底面正方形的边长=周长÷4,也就是通风管的宽和高。
(2)通风管是没有两个底面的,所以求制作通风管需要的材料面积,就是求其侧面积。因为侧面展开后是正方形,正方形边长为36cm,根据正方形面积=边长×边长,即为这个通风管需要的材料。
【详解】(1)(cm)
所以这个通风管的宽和高都是9cm。
(2)()
所以制作这个通风管需要1296。
13.105
【分析】根据题意,如果去掉最右边的一个正方体,表面积就比原来减少30cm2,减少的是正方体的4个面(即上下面、前后面)的面积,用减少的表面积除以4,求出正方体一个面的面积;
用三个同样大小的正方体拼成的一个长方体,那么长方体的表面积等于(3×4+2)个正方形的面积之和,再乘一个面的面积,即是原来长方体的表面积。
【详解】如图:
正方体一个面的面积:30÷4=7.5(cm2)
7.5×(3×4+2)
=7.5×(12+2)
=7.5×14
=105(cm2)
原来长方体的表面积是105cm2。
14.4
【分析】将一个物体放入长方体容器中,水面上升的高度对应的体积就是这个物体的体积。题中放入正方体棱长是6厘米,超过了水深2厘米,则这个正方体只有一部分没入水中。而容器内水得体积没有发生变化,在放入正方体铁块后,水面升高,长方体容器的底面积减少了正方体铁块的一个面的面积,据此求出长方体容器内水的体积,再除以变化后的底面积可得到水深。
【详解】放入物体后水深是:
72×2÷(72-6×6)
=72×2÷(72-36)
=72×2÷36
=4(厘米)
即这时的水深是4厘米。
15.2000
【分析】已知该长方体有两个相对面是正方形,所以其余4个面是完全相同的长方形。根据正方形面积公式,由已知边长算出两个正方形面的面积和;用长方体表面积减去两个正方形面面积和,得到四个相同长方形面的总面积,将长方形面总面积除以4,得到一个长方形面的面积;根据长方形面积公式,由长方形面的面积和已知边长算出长方体的高;依据长方体体积公式“长方体体积=长×宽×高”,代入长、宽、高数值算出体积。
【详解】10×10×2
=100×2
=200(平方厘米)
1000-200=800(平方厘米)
800÷4=200(平方厘米)
200÷10=20(厘米)
10×10×20
=100×20
=2000(立方厘米)
所以该长方体的体积是2000立方厘米。
16. 340 400
【分析】根据、,代入数据计算即可。
【详解】
(平方厘米)
(立方厘米)
一个长方体长10厘米,宽8厘米,高5厘米,表面积是340平方厘米,体积是400立方厘米。
17. 56 24
【分析】拼成的长方体的长是2×3=6分米,宽是2分米,高是2分米的长方体;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高),长方体的体积公式:体积=长×宽×高,代入数据,即可解答。
【详解】拼成的长方体的长:2×3=6(分米),宽是2分米,高是2分米。
(6×2+6×2+2×2)×2
=(12+12+4)×2
=(24+4)×2
=28×2
=56(平方分米)
6×2×2
=12×2
=24(立方分米)
把3个棱长2分米的正方体拼成一个长方体,长方体的表面积是56平方分米,体积是24立方分米。
18.54
【分析】长方体表面积等于前后左后四个侧面面积之和加上上下两个底面面积。要想求这个长方形木箱的底面积,只需用表面积减去侧面积除以2;先求出侧面积,只需要根据S侧面积=C底面周长×h计算,据此解答。
【详解】3米=30分米
(258-30×5)÷2
=(258-150)÷2
=108÷2
=54(平方分米)
故这个木箱的底面积是54平方分米。
19.128
【分析】两个正方体拼成长方体时,两个正方体相接触的面重合,表面积减少的部分就是2个正方形的面积;已知正方体棱长,根据正方形面积公式可算出一个面的面积,用一个面的面积乘2,就能得出减少的表面积。
【详解】8×8×2
=64×2
=128(平方厘米)
所以表面积减少128平方厘米。
20.12
【分析】正方体有6个完全相同的正方形面,其表面积等于6个面的面积总和,公式为S=6a2, 已知正方体木块表面积,要求木块在桌面上所占面积,也就是求正方体其中一个面的面积,只需用正方体的表面积除以6即可。
【详解】72÷6=12(平方分米)
所以木块在桌面上所占的面积是12平方分米。
21. 12 6
【分析】由题意可知,铁丝的总长度就是正方体或者长方体的棱长总和,“棱长=正方体的棱长之和÷12”“高=长方体的棱长之和÷4-长-宽”,把题目中的数据代入公式计算,据此解答。
【详解】144÷12=12(厘米)
144÷4-20-10
=36-20-10
=6(厘米)
所以,正方体的棱长是12厘米,长方体的高是6厘米。
22.12.5
【分析】从题意可知:油箱里的油为长2.5分米,宽为2.5分米,高为2分米的长方体。根据长方体的体积(容积)=长×宽×高,代入数据计算即可。结果换算成升(1升=1立方分米)。
【详解】2.5×2.5×2=12.5(立方分米)
12.5立方分米=12.5升
这个油箱里有油12.5升。
23. 208cm2/208平方厘米 192cm3/192立方厘米
【分析】观察可知,长方体的长是8cm,宽是6cm,高是(cm),根据、,分别代入数据计算即可得解。
【详解】
(cm)
(cm2)
(cm3)
下图是一个长方体的表面展开图,这个长方体的表面积是208cm2,体积是192cm3。
24. 400 144 3600
【分析】长方体共有6个面,每个面都可能是底面,分别为前面、后面、左面、右面、上面和下面,其中前面和后面的面积相同,左面和右面的面积相同,上面和下面的面积相同,根据长方形的面积=长×宽,分别计算出前面、左面和上面的面积,再进行比较即可求出占地面积的最大值、最小值;
根据长方体的体积=长×宽×高,代入数据计算即可解答。
【详解】25×16=400(平方厘米)
25×9=225(平方厘米)
16×9=144(平方厘米)
400>225>144
25×16×9
=400×9
=3600(立方厘米)
所以它的占地面积最大是400平方厘米,最小是144平方厘米,体积是3600立方厘米。
25. 48 4
【分析】长方体框架的棱长总和就是这根铁丝的长,根据长方体的棱长总和=(长+宽+高)×4,代入数据计算即可求出这根铁丝的长;正方体的棱长总和=棱长×12,用这根铁丝的长除以12就是正方体的棱长。
【详解】(6+4+2)×4
=(10+2)×4
=12×4
=48(分米)
48÷12=4(分米)
所以这根铁丝长48分米,如果改做成一个正方体框架,棱长是4分米。
26.908
【分析】要想使打包得到的长方体表面积最小,就应使对接的全等的面的面积尽可能地大,因此首先两盒之间应以11×7的面对接,先组装成两个相同的长方体,其体积皆为11×7×(2×6)=11×7×12。由于12×7>11×7,因此这个组成的长方体对接面是12×7的两个面,如图
,根据长方体表面积=(长×宽+长×高+宽×高)×2,列式计算即可。
【详解】7+7=14(厘米)
(14×11+14×12+11×12)×2
=(154+168+132)×2
=454×2
=908(平方厘米)
按“规则方式”打包得到的长方体的表面积的最小值是908平方厘米。
27. 9 2
【分析】正方体展开图符合“2-2-2”型结构,折成正方体后,“1”对“5”,“2”对“4”,“3”对“6”,据此求出相对两个数的和与差,进而解答。
【详解】根据分析可知,折成正方体后,“1”对“5”,“2”对“4”,“3”对“6”。
1+5=6;5-1=4
2+4=6;4-2=2
3+6=9;6-3=3
和最大是9,差最小是2。
一个正方体的展开图,六个面上分别写有这六个数字,相对的两个面上数字的和最大是9,相对的两个面上数字的差最小是2。
28.爱
【分析】结合3种摆放情况可知,“南”对面不可能“小”,“活”、“狮”、“生”,所以“南”对面是“爱”,据此解答。
【详解】根据分析可知,一个正方体木块六个面上分别写上小、南、狮、爱、生、活这六个汉字。从不同角度看这个正方体,如图所示,通过推断可知“南”的对面是“爱”。
29. 64 32
【分析】根据题意可知:这个长方体盒子的侧面展开是一个边长8厘米的正方形,长方体的侧面积=底面周长×高,由此可知,这个长方体的底面周长和高都是8厘米,又已知底面是正方形,根摇正方形的周长公式:C=4a,那么a=C÷4,据此求出底面边长,然后根据长方体的体积公式:V=abh,把数据代入公式解答。
【详解】8×8=64(平方厘米)
8÷4=2(厘米)
2×2×8
=4×8
=32(立方厘米)
这个长方体的侧面积是64平方厘米,体积是32立方厘米。
30. 15 125 A B
【分析】根据题意可知,长方形的长和宽分别被正方体的边长平均分成4份和3份,那么长方形的长等于正方体边长的4倍,据此可求出正方体边长是5厘米,宽是边长的3倍,再根据V=a×a×a计算体积即可。折成正方体后D和A相对,C和E相对,B和F相对。再根据题中的摆放方式,找到右面的面是哪一面,据此解答。
【详解】20÷4×3
=5×3
=15(厘米)
5×5×5
=25×5
=125(立方厘米)
正方体展开图是2-3-1型,折成正方体后D和A相对,C和E相对,B和F相对。摆放如下图。
故长方形宽是15厘米,盒子体积是125立方厘米,和D面相对的是A面,如果D面是底面,从前面看是C面,那么右面是B面。
31. 20 60 74
【分析】观察图形可知,长方体玻璃容器的长可以摆5个,宽摆4个,根据长方形面积公式:面积=长×宽,据此求出一层可以摆小正方体的个数;
长方体容器的长摆5个,宽摆4个,高摆3个;根据长方体容积公式:容积=长×宽×高,代入数据,即可求出长方体容器可以摆小正方体的数量;
求做这个容器需要玻璃的面积,就是求长方体容器的5个面积的面积和;根据长方体5个面的表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,即可解答。
【详解】5×4=20(个)
5×4×3
=20×3
=60(个)
长:1×5=5(厘米);宽:1×4=4(厘米);高:1×3=3(厘米)
5×4+(5×3+4×3)×2
=20+(15+12)×2
=20+27×2
=20+54
=74(平方厘米)
在一个无盖的长方体玻璃容器内摆棱长为1厘米的小正方体,一层可以摆20个,一共可以摆60个,做这个容器需要玻璃74平方厘米。
32. 32 18
【分析】(1)观察可知,上下、左右各有5个小正方形,前后各有6个小正方形,根据,小正方体的每个面的面积是(平方厘米),用每个面的面积乘小正方形的总个数即可。
(2)观察可知,要搭一个大正方体,每条棱长最多有3个小正方体,即搭成的大正方体的棱长至少是3厘米,根据,代入数据可计算搭成的大正方体的体积及小正方体的体积,用大正方体体积除以小正方体体积,得到搭成的大正方体需要多少个小正方体,再减图中小正方体的个数即可得解。
【详解】
(平方厘米)
(个)
用棱长1厘米的小正方体搭成如图所示的图形,它的表面积是32平方厘米;至少再添加18个同样的小正方体,才能搭成一个大正方体。
33.10
【分析】根据正方体的体积公式:体积=棱长×棱长×棱长,代入数据,分别求出大正方体和小正方体的体积,再用大正方体的体积除以小正方体的体积,即可求出可以切成多少块小正方体,最后用小正方体的棱长×小正方体的个数,即可解答,注意单位名数的换算。
【详解】1厘米=0.01米
(1×1×1)÷(0.01×0.01×0.01)
=(1×1)÷(0.0001×0.01)
=1÷0.000001
=1000000(块)
0.01×1000000=10000(米)
10000米=10千米
把棱长1米的正方体切割成棱长1厘米的小正方体,把这些小正方体一个挨一个地连起来,可以排10千米。
34.2
【分析】正方体的特征:6个面都是正方形,且面积相等。正方体的展开图折成正方体时,相对的面不相邻。想象把正方体展开图折成正方体,取相对的面即可。
【详解】把正方体展开图折成一个正方体,可以想象成:3是下面,2是后面,1是左面,4是右面,5是上面,6是前面。
所以,这个正方体的6号面的对面是2号面。
35. ② ④
【分析】分析题目,根据正方形的面积=边长×边长可知小正方体每个面的面积是1×1=1(dm2),剩下部分图形的表面积比原来的大长方体的表面积增加4dm2,就是增加了4÷1=4(个)小正方形的面,据图可知,拿掉①或⑤表面积不变,拿掉②、③或④表面积都会增加2个面,拿掉中间相邻的两个②③或③④表面积会增加2个小正方形,拿掉中间不相邻的两个②和④表面积会增加4个小正方形,所以表面积想增加4dm2,得拿中间的,并隔一个拿一个,据此解答。
【详解】1×1=1(dm2)
4÷1=4(个)
根据分析,使所剩部分的表面积比原来长方体的表面积增加4dm2,拿②和④。
淘气用棱长1dm的小正方体拼成一个长方体。他要从5个有编号的小正方体中拿掉2个,使剩下图形的表面积比原来图形的表面积增加4dm2,他拿掉的小正方体编号可能是②和④。
36. 60 40
【分析】把一个长方体切开后,表面积会增加切面面积的两倍,要求表面积最多增加多少,说明切的那个面的面积必须最大;要求表面积最少增加多少,说明切的那个面的面积必须最小,由此找出长方体中最大面和最小面的面积,即可解答本题。
【详解】最大:(平方厘米)
最小:(平方厘米)
表面积最多可以增加60平方厘米,最少可以增加40平方厘米。
【点睛】本题考查了长方体切割后的图形的表面积计算,沿平行于宽高面切割,可使两个长方体的表面积之和最小;沿平行于长宽面切割,可使两个长方体的表面积之和最大。
37.160
【分析】通过观察图形可知,把2个棱长4分米的正方体拼成一个长方体,拼成的长方体的表面积比两个正方体的表面积和减少了正方体的2个面的面积(即重叠在一起的两个面),根据正方体的表面积公式:,把数据代入公式解答。
【详解】
(平方分米)
故拼成的长方体的表面积是160平方分米。
38.5
【分析】根据“正方体体积表示棱长)”计算出棱长是10厘米的正方体容器装满水后水的体积。注意水的体积不发生改变,再根据“长方体体积表示底面的长,表示底面的宽,表示高)”,即用正方体容器水的体积除以长方体底面积即可求出长方体水深。
【详解】
(厘米)
则此时长方体容器水深5厘米。
39.288
【分析】根据题意可知,增加的表面积等于4个长等于长方体的宽,宽等于长方体的高的长方形,用增加的面积÷4,求出一个面的面积,也就是长方体的底面积,再根据长方体体积公式:体积=底面积×高,代入数据,即可解答,注意单位名数的统一。
【详解】2.4m=24dm
48÷4×24
=12×24
=288(dm3)
原来长方体木料的体积是288dm3。
40. 158 52
【分析】长方体表面积(长宽长高宽高),代入数据计算即可解答第一个空;如果高减少2分米,即减少了长是8分米、宽是2分米的2个长方形的面积与长是5分米、宽是2分米的2个长方形的面积和,据此解答第二个空。
【详解】
(平方分米)
(平方厘米)
所以,一个长方体长8分米,宽5分米,高3分米,它的表面积是158平方分米,如果高减少2分米,表面积减少52平方分米。
41.0.006
【分析】根据切割方法,锯成两段时,表面积增加了2个横截面的面积,据此即可求出横截面的面积是(平方厘米),再根据长方体体积底面积高,用长方体木料的底面积乘木料的长,即可求出它的体积。
【详解】(平方厘米)
20平方厘米(平方米)
(立方米)
这根木料的体积是0.006立方米。
【点睛】解答此题的关键是根据切割方法,求出长方体木料的横截面的面积。要注意单位的统一。
42.55.5
【分析】沿着长、宽、高垂直各切一刀,表面一共增加了6个面,正好等于原来的表面积,据此分析。
【详解】沿着长、宽、高垂直各切一刀,增加上下、左右、前后6个面的面积,也就是原长方体的表面积。所以表面积比原来增加了55.5平方厘米。
43.22
【分析】根据正方体的表面积棱长棱长6,长方体的表面积(长宽长高宽高),把数据代入公式求出12个正方体的表面积和与长方体的表面积差即可。
【详解】按照图示拼成的长方体的长是12cm,宽和高都是1cm。
(cm2)
则表面积减少了22cm2。
44.
【分析】有大、中、小三个正方形的水池,可知这三个水池底面都是正方形的,把两堆沙分别沉没在中、小水池的水里,可知底面是不变的,只是水面会升高,升高那部分水的体积就是所放沙的体积,利用长方体的体积公式长宽高,求出两堆沙的体积;再将这两堆沙石都倒入大水池的水里,底面变了,体积没变,水面升高的那部分水的体积就是两堆沙的体积,再用两堆沙的体积和除以大正方形水池的底面积,即可解答,注意单位名数的统一。
【详解】2米=200厘米
3米=300厘米
6米=600厘米
200×200×4
=40000×4
=160000(立方厘米)
300×300×6
=90000×6
=540000(立方厘米)
(160000+540000)÷(600×600)
=700000÷360000
=(厘米)
如果把两堆沙都倒入大号水池,大号水池水面上升厘米。
45. 44 16
【分析】小正方体的每个面都是正方形,根据,可求出每个面的面积,观察可知, 这个图形从正面和后面看都有8个面,从上面和下面看都有6个面,从左面和右面看都有8个面,用每个面的面积乘面的总数可得这个图形的表面积。
观察可知这个图形一共有16个小正方体,根据,代入数据计算小正方体的体积,再用小正方体的体积乘16,即可得这个图形的体积。
【详解】
(平方厘米)
(立方厘米)
用棱长为1厘米的小正方体拼成下面的图形,这个图形的表面积是44平方厘米,体积是16立方厘米。
46. 15 46
【分析】根据正方体的体积公式V=a3,可知棱长1厘米的正方体的体积是1立方厘米;从图中数出正方体的个数,再乘用正方体的体积,即是这个几何体的体积。
已知正方体的棱长是1厘米,那么正方体一个面的面积是1平方厘米。求这个几何体的表面积,就是求露出正方体的面的面积之和,分别数出从上下面、前后面、左右面看到的小正方形的个数,再乘一个面的面积即可。
【详解】1×1×1×15=15(立方厘米)
(9+7+7)×2
=23×2
=46(个)
1×1×46=46(平方厘米)
它的体积是15立方厘米,表面积是46平方厘米。
47. 22 46
【分析】通过观察图形可知,需要胶带的长度等于这个包装箱的2条长加上2条宽再加上4条高的长度,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式求出需要硬纸板的面积。
【详解】4×2+2×2+2.5×4
=8+4+10
=12+10
=22(分米)
(4×2+4×2.5+2×2.5)×2
=(8+10+5)×2
=23×2
=46(平方分米)
至少需要胶带22分米,做这个包装箱至少需要硬纸板46平方分米。
48.9
【分析】根据题意可知,把这个长方体木料横截成3段,表面积比原来增加了4个截面的面积,据此可以求出一个截面的面积,再根据长方体的体积公式:V=Sh,把数据代入公式解答。
【详解】1.5米=15分米
2.4÷4×15
=0.6×15
=9(立方分米)
原来这根木料的体积9立方分米。
49. 700 1000
【分析】看图可知,正方形纸板的边长包含2条高和2条宽,宽是高的2倍,根据和倍问题的解题方法,正方形边长÷(1+1+2+2)=高,高×2=宽,正方形边长-高×2=长,据此确定长方体的长、宽、高。根据长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,列式计算即可。
【详解】高:30÷(1+1+2+2)
=30÷6
=5(厘米)
宽:5×2=10(厘米)
长:30-5×2
=30-10
=20(厘米)
表面积:(20×10+20×5+10×5)×2
=(200+100+50)×2
=350×2
=700(平方厘米)
体积:20×10×5=1000(立方厘米)
它的表面积是700平方厘米,体积是1000立方厘米。
【点睛】关键是掌握和倍问题的解题方法,先确定长、宽、高,再灵活运用长方体表面积和体积公式。
50. 96 3.76 480
【分析】求铁丝的长其实就是求长方体的棱长总和,根据长方体的棱长总和=(长+宽+高)×4,代入数据计算即可。求彩纸的面积就是求长方体的表面积,根据,代入数据计算即可。再根据,计算可得长方体所占的空间。单位不同要统一单位。
【详解】
(厘米)
(平方厘米)
(平方分米)
(立方厘米)
用铁丝围成一个长方体框架,长10厘米,宽8厘米,高6厘米,铁丝长96厘米;如果给它各个面蒙上彩纸,至少要3.76平方分米的彩纸;这个长方体所占的空间是480立方厘米。
51.18
【分析】底面是正方形的长方体,侧面展开是周长16分米的正方形,由此可知,周长16分米的正方形的边长等于底面正方形的周长、等于原长方体的高,由正方形的周长=边长×4,用16÷4求出原长方体的高,再用原长方体的高除以4求出底面正方形的边长,该长方体的表面积=侧面积+底面正方形面积的2倍,侧面积=边长是16÷4=4(分米)的正方形的面积,根据正方形的面积=边长×边长解答。
【详解】16÷4÷4
=4÷4
=1(分米)
1×1×2+(16÷4)×(16÷4)
=2+4×4
=2+16
=18(平方分米)
所以它的表面积是18平方分米。
52.200
【分析】根据题意,把长方体木料锯成4段,要截3次;每截一次增加2个截面,截3次增加6个截面,表面积会增加6个截面的面积;
先用增加的表面积除以6,求出一个截面的面积;再根据长方体的体积公式V=Sh,求出原来木料的体积。注意单位的换算:1米=10分米。
【详解】2.5米=25分米
增加截面的个数:
(4-1)×2
=3×2
=6(个)
截面的面积:48÷6=8(平方分米)
体积:8×25=200(立方分米)
原来这根木料的体积是200立方分米。
53.5
【分析】根据题意,作图如下:
从“一个长方体,如果高增加3厘米,就变成一个正方体”可知:这个长方体的高+3厘米=长=宽=正方体的棱长。高增加3厘米,就从长方体变成正方体,上下面不变,前后左右4个面共增加了96平方厘米,用96÷4=24平方厘米求出一个面增加的面积。再用一个面增加的面积÷3即可得正方体的棱长,用棱长减去3就得长方体的高。
【详解】96÷4÷3-3
=8-3
=5(厘米)
原来长方体的高是5厘米。
54.16
【分析】根据题意,结合正方体的体积公式:边长×边长×边长,先求出正方体的边长,再结合底面积=边长×边长,代入数据计算即可。
【详解】64=4×4×4
4×4=16(平方分米)
所以它的底面积是16平方分米。
55.85
【分析】求鱼缸玻璃和水的接触面积,实际上就是求由水组成的长5分米、宽5分米、高3分米的长方体的5个面的面积,再结合长方体表面积的计算公式即可求解。
【详解】(5×3+5×3)×2+5×5
=(15+15)×2+5×5
=30×2+5×5
=60+25
=85(平方分米)
则与水接触的玻璃的面积是85平方分米。
56.4800
【分析】求铁皮的面积就是求长方体的侧面积,根据长方体的侧面积=底面周长×高,据此进行计算即可。
【详解】1.2米=120厘米
10×4×120
=40×120
=4800(平方厘米)
则至少需要铁皮4800平方厘米。
57. 4 20
【分析】求蓄水箱的占地面积就是求边长为2米的正方形的面积,根据正方形的面积=边长×边长,据此计算即可;求无盖正方体蓄水箱需要的铁皮就是求正方体五个面的面积,根据正方体五个面的面积=一个面的面积×5,据此进行计算即可。
【详解】2×2=4(平方米)
2×2×5
=4×5
=20(平方米)
则它的占地面积是4平方米,制作一个至少需要20平方米铁皮。
58.2ab
【分析】根据题意,一个长为a米、宽为b米的长方体的高增加2米,那么增加的体积就是高为2米的长方体的体积,根据长方体的体积=长×宽×高,即可求出比原来增加的体积。
【详解】a×b×2=2ab(立方米)
体积比原来增加2ab立方米。
59. 1000000 9
【分析】先根据正方体的体积公式V=a3,求出棱长为1m和棱长为1cm的大、小正方体的体积,再用大正方体的体积除以小正方体的体积,即是一共能切成小正方体的块数;
把棱长1cm的小正方体木块排成一排,用小正方体的棱长乘小正方体的块数,求出排成一排的距离,再减去1km即可。
注意单位的换算:1m=100cm,1km=100000cm。
【详解】1m=100cm
(100×100×100)÷(1×1×1)
=1000000÷1
=1000000(块)
1000000×1=1000000(cm)
1000000cm=10km
10-1=9(km)
一共能切(1000000)块,把它们排成一排,排成的距离比1km多(9)km。
60.8.064
【分析】要求这个水泥池的容积,需要知道水泥池里面的长、宽和高,所以先求出水泥池的长和宽,分别减去两个墙厚即可,高不变,然后用长方体容积公式:容积=长×宽×高,代入数据,就可求出体积,注意单位名数的统一。
【详解】10cm=0.1m
(3-0.1×2)×(2-0.1×2)×1.6
=(3-0.2)×(2-0.2)×1.6
=2.8×1.8×1.6
=5.04×1.6
=8.064(m3)
这个水池的容积是8.064m3。
答案第24页,共24页
答案第23页,共23页
1.在括号里填上合适的单位。
一台家用冰箱的容积大约是450( ) 一个游泳池可装水2500( )
教室的面积约是80( ) 40.4立方米=( )立方分米
6500毫升=( )立方厘米=( )立方分米
2.一个杯子最多能装250mL,是指杯子的( )是250mL。
3.一个正方体相对两个面上的数互为倒数,如图是它的展开图,A面上的数是( ),抛起这个正方体,落下后整数朝上的可能性比分数朝上的可能性( )。(填“大”“小”或“相等”)
4.一个长4分米,宽2分米,高4分米的长方体,它的占地面积最大是( ),它的表面积是( )。
5.一个正方体的棱长是4分米,它的表面积是( )。
6.正方体有( )个面,( )条棱,( )个顶点,从不同的角度最多能看到( )个面。
7.长方体有( )个顶点,( )条棱,包含( )组相对的棱,( )组相对的面,相对的面( ),相交于同一个顶点的三条棱的长度分别叫作长方体的( )、( )、( )。
8.把一根长3.5dm的长方体木料截成6段(如图),表面积比原来增加了,这根木料原来的体积是( )。
9.一个正方体的棱长是5厘米,它的体积是( )立方厘米。
10.一个棱长是4dm的正方体水箱中装有半箱水。把一块铁块完全浸入水中,水面上升了6cm,这个铁块的体积是( )。
11.一个长方体的玻璃鱼缸,长60厘米,宽5分米,高4分米,这个玻璃鱼缸的体积是( )。
12.一个横截面是正方形的长方体通风管长36cm,其侧面展开后恰好是一个正方形(如图),这个通风管的宽和高都是( )cm,制作这个通风管需要( )的材料。
13.一个长方体是由三个同样大小的正方体拼成的,如果去掉最右边的一个正方体,表面积就比原来减少30cm2,原来长方体的表面积是( )cm2。
14.在一个底面积72平方厘米、高10厘米的长方体容器中,水深2厘米。如果放入一个棱长6厘米的正方体铁块,这时水深( )厘米。
15.一个长方体,其中两个相对的面为边长10厘米的正方形,这个长方体的表面积是1000平方厘米,它的体积是( )立方厘米。
16.一个长方体长10厘米,宽8厘米,高5厘米,表面积是( )平方厘米,体积是( )立方厘米。
17.把3个棱长2分米的正方体拼成一个长方体,长方体的表面积是( )平方分米,体积是( )立方分米。
18.一个长方体木箱,底面周长是3米,高5分米,表面积是258平方分米。这个木箱的底面积是( )平方分米。
19.把两个棱长8厘米的正方体拼成一个长方体后,表面积减少( )平方厘米。
20.把一个表面积是72平方分米的正方体木块放在桌面上,木块在桌面上所占的面积是( )平方分米。
21.用一根长144厘米的铁丝围成一个正方体框架,棱长是( )厘米;如果用它围成一个长方体框架,长是20厘米,宽是10厘米,那么高是( )厘米。
22.一个正方体铁皮油箱的棱长为2.5分米,如果里面的油深2分米,这个油箱里有油( )升。
23.下图是一个长方体的表面展开图,这个长方体的表面积是( ),体积是( )。
24.一个长方体长25厘米,宽16厘米,高9厘米,它的占地面积最大是( )平方厘米,最小是( )平方厘米,体积是( )立方厘米。
25.用一根铁丝正好能做成一个长6分米、宽4分米、高2分米的长方体框架,这根铁丝长( )分米;如果改做成一个正方体框架,棱长是( )分米。
26.12盒磁带按“规则方式”打包,所谓“规则方式”是指每相邻两盒必须是以全等的面积对接,最后得到的包装形状是一个长方体。已知磁带盒的长为11厘米,宽为7厘米,高为2厘米。按“规则方式”打包得到的长方体的表面积的最小值是( )平方厘米。
27.如图是一个正方体的展开图,六个面上分别写有这六个数字,相对的两个面上数字的和最大是( ),相对的两个面上数字的差最小是( )。
28.一个正方体木块六个面上分别写上小、南、狮、爱、生、活这六个汉字。从不同角度看这个正方体,如图所示,通过推断可知“南”的对面是( )。
29.一个底面是正方形的长方体盒子,侧面展开图是一个边长为8厘米的正方形,这个长方体的侧面积是( )平方厘米,体积是( )立方厘米。
30.一张长方形铁皮(如图),长是20厘米,宽是( )厘米。用图中的阴影部分向里折成一个正方体盒子,盒子的体积是( )立方厘米。和D面相对的是( )面;如果D面是底面,从前面看是C面,那么右面是( )面。
31.在一个无盖的长方体玻璃容器内摆棱长为1厘米的小正方体(如图),一层可以摆( )个,一共可以摆( )个,做这个容器需要玻璃( )平方厘米。(玻璃厚度忽略不计)
32.用棱长1厘米的小正方体搭成如图所示的图形,它的表面积是( )平方厘米;至少再添加( )个同样的小正方体,才能搭成一个大正方体。
33.把棱长1米的正方体切割成棱长1厘米的小正方体,把这些小正方体一个挨一个地连起来,可以排( )千米。
34.将下图沿虚线折成一个正方体,这个正方体的6号面的对面是( )号面。
35.如图,淘气用棱长是1dm的小正方体拼成一个长方体。他要从5个有编号的小正方体中拿掉2个,使剩下图形的表面积比原来图形的表面积增加4dm2,他拿掉的小正方体编号可能是( )和( )。
36.把一个长、宽、高分别为6厘米、5厘米、4厘米的长方体切成两个完全相同的长方体,表面积最多可以增加( )平方厘米,最少可以增加( )平方厘米。
37.把2个棱长4分米的正方体拼成一个长方体(如图),拼成的长方体的表面积是( )平方分米。
38.将一个棱长是10厘米的正方体容器装满水,再把水全部倒入长20厘米,宽10厘米的长方体容器。此时长方体容器水深( )厘米。
39.如图,王师傅把长的长方体木料锯成3个相同的小长方体,表面积增加了,原来长方体木料的体积是( )。
40.一个长方体长8分米,宽5分米,高3分米,它的表面积是( )平方分米。如果高减少2分米,表面积减少( )平方分米。
41.把一根长3米的长方体木料沿与长垂直的截面锯成两段,锯开后两段木料的表面积之和比原来木料的表面积增加了40平方厘米。这根木料的体积是( )立方米。
42.把一个表面积是55.5平方厘米的长方体,沿着长、宽、高垂直各切一刀后分成了8个小长方体(如图),表面积比原来增加了( )平方厘米。
43.12个棱长的正方体,如图继续拼下去,拼成的新长方体,表面积减少了( )。
44.有小中大三个正方体水池,从里面测量它们的边长分别是2米、3米、6米,把两堆沙分别倒入小、中号水池,水面分别上升了4厘米、6厘米,如果把两堆沙都倒入大号水池,大号水池水面上升( )厘米。
45.用棱长为1厘米的小正方体拼成下面的图形,这个图形的表面积是( )平方厘米,体积是( )立方厘米。
46.如图是用棱长1厘米的正方体木块摆成的几何体,它的体积是( )立方厘米,表面积是( )平方厘米。
47.一个包装箱长4分米、宽2分米、高2.5分米,王师傅用胶带缠绕进行打包(如图所示),至少需要胶带 分米;做这个包装箱至少需要硬纸板 平方分米。
48.把长1.5米的长方体材料(如图),平均锯成3段,表面积比原来增加2.4平方分米,原来这根木料的体积是 立方分米。
49.如图1是边长为30厘米的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体纸盒。已知该长方体的宽是高的2倍,则它的表面积是( )平方厘米,体积是( )立方厘米。
50.用铁丝围成一个长方体框架,长10厘米,宽8厘米,高6厘米,铁丝长( )厘米;如果给它各个面蒙上彩纸,至少要( )平方分米的彩纸;这个长方体所占的空间是( )立方厘米。
51.底面是正方形的长方体,侧面展开是周长16分米的正方形,它的表面积是( )平方分米。
52.把一根 2.5米长的长方体木料垂直于长锯成4段,表面积增加48平方分米。原来这根木料的体积是( )立方分米。
53.一个长方体,如果高增加3厘米,就变成一个正方体。这时表面积比原来增加了96平方厘米。原来长方体的高是( )厘米。
54.一个正方体的体积是64立方分米,它的底面积是( )平方分米。
55.一个无盖的长方体玻璃鱼缸,长和宽都是5分米,高4分米,在里面倒入高3分米的水,与水接触的玻璃的面积是( )平方分米。
56.做一节长1.2米,宽和高都是10厘米的通风管,至少需要铁皮( )平方厘米。
57.一个棱长是2米的无盖正方体蓄水箱,它的占地面积是( )平方米,制作一个至少需要( )平方米铁皮。
58.如图,一个长方体的长、宽、高分别是a米、b米、h米。如果高增加2米,体积比原来增加( )立方米。
59.把棱长1m的正方体木块切成棱长1cm的小正方体木块,一共能切( )块,把它们排成一排,排成的距离比1km多( )km。
60.如下图,在一块平坦的地面上,实践社团的同学们在工人师傅的帮助下,用砖围了一个长方体水池,池壁厚10(底面利用原有的水泥地)。这个水池的容积是( )。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第2页,共7页
第7页,共7页
《2025-2026学年苏教版六年级上册数学第一单元长方体和正方体高频填空题》参考答案
1. 升/L 立方米/m3 平方米/m2 40400 6500 6.5
【分析】容积单位有升(L)、毫升(mL),家用冰箱容积较大,用升作单位合适。比如常见的小型家用双门冰箱容积大概300~500升。
游泳池装水量很大,体积单位用立方米(m3)合适。比如一个小型游泳池一般能装水几千立方米,2500立方米符合小型游泳池的规模。
面积单位有平方米(m2)、平方分米等,教室面积用平方米衡量合适。比如一间卧室的面积是60平方米。
1立方米=1000立方分米,大单位换小单位乘进率。
1毫升=1立方厘米,所以6500毫升=(6500)立方厘米。1立方分米=1000立方厘米,小单位换大单位除以进率。
【详解】家用冰箱容积较大,用升作单位合适。一台家用冰箱的容积大约是450升(L)。
游泳池装水量很大,用立方米作单位合适。一个游泳池可装水2500立方米(m3)。
教室面积用平方米衡量合适。教室的面积约是80平方米(m2)。
1立方米=1000立方分米
40.4×1000=40400(立方分米)
40.4立方米=40400立方分米
1毫升=1立方厘米
6500毫升=6500立方厘米
1立方分米=1000立方厘米
6500÷1000=6.5(立方分米)
6500毫升=6500立方厘米=6.5立方分米
2.容积
【分析】杯子的“最多能装250mL”指的是它内部所能容纳液体的最大体积,根据数学定义,容器能容纳物体的体积称为“容积”。
【详解】题目中描述杯子“最多能装250mL”,这里的“装”指杯子内部可以容纳的液体量。容器所能容纳物体的体积称为容积。
所以,一个杯子最多能装250mL,是指杯子的容积是250mL。
3. 大
【分析】观察展开图,折成正方体后,A面与3面相对(通过空间想象,把展开图还原成正方体,可确定3和A是对面)。然后根据倒数的定义确定具体的数。
可能性大小与数量多少有关,数量越多,朝上的可能性越大;先确定整数面和分数面的数量。相对面情况:3和A()相对、2和B相对、1和C相对。因为2的倒数是,所以B=;1的倒数是1,所以C=1。那么6个面的数分别是3(整数)、(分数)、2(整数)、(分数)、1(整数)、1(整数)。统计整数面和分数面数量:整数面有3、2、1、1,共4个;分数面有、,共2个。然后比较大小即可解答。
【详解】
所以A面上的数是。
整数面有3、2、1、1,共4个;分数面有、,共2个。
4>2
A面上的数是,抛起这个正方体,落下后整数朝上的可能性比分数朝上的可能性大。
4. 16平方分米 64平方分米
【分析】求它占地面积就是求的底面积,当以长4分米、高4分米为底面时的占地面积最大,根据长方形的面积=长×宽,长方体的表面积=(长×宽+宽×高+长×高)×2解答。
【详解】4×4=16(平方分米)
(4×2+2×4+4×4)×2
=(8+8+16)×2
=(16+16)×2
=32×2
=64(平方分米)
所以占地面积最大是16平方分米,表面积是64平方分米。
5.96平方分米/96dm2
【分析】根据正方体的表面积=棱长×棱长×6,代入数据计算即可。
【详解】4×4×6
=16×6
=96(平方分米)
所以表面积是96平方分米。
6. 6 12 8 3
【分析】正方体特征:有6个面都是正方形,且面积相等;有8个顶点;有12条棱且长度都相等。从不同的角度看正方体,最少能看到1个面,最多能看到3个面。据此解答。
【详解】正方体有6个面,12条棱,8个顶点,从不同的角度最多能看到3个面。
7. 8 12 3 3 完全相同 长 宽 高
【详解】长方体有8个顶点,12条棱,包含3组相对的棱,3组相对的面,相对的面完全相同,相交于同一个顶点的三条棱的长度分别叫作长方体的长、宽、高。
8.87.5dm3/87.5立方分米
【分析】把长方体木料截成6段,需要截的次数为6-1=5次。每截1次会增加2个截面的面积,那么截5次增加的截面数量是5×2=10个。已知表面积比原来增加了250dm2,增加的面积就是10个截面的面积之和,而每个截面的面积都等于长方体木料的底面积,所以木料的底面积为250÷10=25dm2。根据长方体体积公式V=Sh(其中V表示体积,S表示底面积,h表示高),已知木料长3.5dm,也就是高h=3.5dm,底面积S=25dm2,把数据代入公式计算即可。
【详解】6-1=5(次)
5×2=10(个)
250÷10=25(dm2)
25×3.5=87.5(dm3)
这根木料原来的体积是87.5dm3或87.5立方分米。
9.125
【分析】正方体的体积公式为V=a3(V代表体积,a为棱长),已知正方体的棱长是5厘米,把数据代入公式即可解答。
【详解】53
=5×5×5
=125(立方厘米)
它的体积是125立方厘米。
10.9.6
【分析】当把铁块完全浸入水中时,水面上升,上升的这部分水的形状为长方体,而铁块的体积就等于上升的这部分水的体积。已知正方体水箱棱长是4dm,水面上升了6cm,1dm=10cm,可得6cm为6÷10=0.6dm。上升的水的形状为长方体,该长方体的长和宽就是正方体水箱的棱长4dm,高为水面上升的高度0.6dm。根据长方体体积公式V=a×b×h(其中V表示体积,a表示长,b表示宽,h表示高),把数据代入公式可得上升的水的体积(即铁块体积)。
【详解】1dm=10cm
6÷10=0.6(dm)
4×4×0.6=9.6(dm3)
所以这个铁块的体积是9.6dm3。
11.120立方分米
【分析】长方体体积的计算公式为V=a×b×h(其中V表示体积,a表示长方体的长,b表示长方体的宽,h表示长方体的高)。已知玻璃鱼缸长60厘米,宽5分米,高4分米,1分米=10厘米,可得60厘米为60÷10=6分米。然后把数据代入公式计算即可解答。
【详解】1分米=10厘米
60÷10=6(分米)
6×5×4=120(立方分米)
这个玻璃鱼缸的体积是120立方分米(dm3)或120000立方厘米(cm3)。
12. 9 1296
【分析】(1)由题意知,通风管的横截面是正方形,侧面展开后恰好是一个正方形,通风管长36cm,即侧面展开图正方形的边长为36cm,而侧面展开图的边长也等于底面正方形的周长,即可求出底面正方形的边长=周长÷4,也就是通风管的宽和高。
(2)通风管是没有两个底面的,所以求制作通风管需要的材料面积,就是求其侧面积。因为侧面展开后是正方形,正方形边长为36cm,根据正方形面积=边长×边长,即为这个通风管需要的材料。
【详解】(1)(cm)
所以这个通风管的宽和高都是9cm。
(2)()
所以制作这个通风管需要1296。
13.105
【分析】根据题意,如果去掉最右边的一个正方体,表面积就比原来减少30cm2,减少的是正方体的4个面(即上下面、前后面)的面积,用减少的表面积除以4,求出正方体一个面的面积;
用三个同样大小的正方体拼成的一个长方体,那么长方体的表面积等于(3×4+2)个正方形的面积之和,再乘一个面的面积,即是原来长方体的表面积。
【详解】如图:
正方体一个面的面积:30÷4=7.5(cm2)
7.5×(3×4+2)
=7.5×(12+2)
=7.5×14
=105(cm2)
原来长方体的表面积是105cm2。
14.4
【分析】将一个物体放入长方体容器中,水面上升的高度对应的体积就是这个物体的体积。题中放入正方体棱长是6厘米,超过了水深2厘米,则这个正方体只有一部分没入水中。而容器内水得体积没有发生变化,在放入正方体铁块后,水面升高,长方体容器的底面积减少了正方体铁块的一个面的面积,据此求出长方体容器内水的体积,再除以变化后的底面积可得到水深。
【详解】放入物体后水深是:
72×2÷(72-6×6)
=72×2÷(72-36)
=72×2÷36
=4(厘米)
即这时的水深是4厘米。
15.2000
【分析】已知该长方体有两个相对面是正方形,所以其余4个面是完全相同的长方形。根据正方形面积公式,由已知边长算出两个正方形面的面积和;用长方体表面积减去两个正方形面面积和,得到四个相同长方形面的总面积,将长方形面总面积除以4,得到一个长方形面的面积;根据长方形面积公式,由长方形面的面积和已知边长算出长方体的高;依据长方体体积公式“长方体体积=长×宽×高”,代入长、宽、高数值算出体积。
【详解】10×10×2
=100×2
=200(平方厘米)
1000-200=800(平方厘米)
800÷4=200(平方厘米)
200÷10=20(厘米)
10×10×20
=100×20
=2000(立方厘米)
所以该长方体的体积是2000立方厘米。
16. 340 400
【分析】根据、,代入数据计算即可。
【详解】
(平方厘米)
(立方厘米)
一个长方体长10厘米,宽8厘米,高5厘米,表面积是340平方厘米,体积是400立方厘米。
17. 56 24
【分析】拼成的长方体的长是2×3=6分米,宽是2分米,高是2分米的长方体;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高),长方体的体积公式:体积=长×宽×高,代入数据,即可解答。
【详解】拼成的长方体的长:2×3=6(分米),宽是2分米,高是2分米。
(6×2+6×2+2×2)×2
=(12+12+4)×2
=(24+4)×2
=28×2
=56(平方分米)
6×2×2
=12×2
=24(立方分米)
把3个棱长2分米的正方体拼成一个长方体,长方体的表面积是56平方分米,体积是24立方分米。
18.54
【分析】长方体表面积等于前后左后四个侧面面积之和加上上下两个底面面积。要想求这个长方形木箱的底面积,只需用表面积减去侧面积除以2;先求出侧面积,只需要根据S侧面积=C底面周长×h计算,据此解答。
【详解】3米=30分米
(258-30×5)÷2
=(258-150)÷2
=108÷2
=54(平方分米)
故这个木箱的底面积是54平方分米。
19.128
【分析】两个正方体拼成长方体时,两个正方体相接触的面重合,表面积减少的部分就是2个正方形的面积;已知正方体棱长,根据正方形面积公式可算出一个面的面积,用一个面的面积乘2,就能得出减少的表面积。
【详解】8×8×2
=64×2
=128(平方厘米)
所以表面积减少128平方厘米。
20.12
【分析】正方体有6个完全相同的正方形面,其表面积等于6个面的面积总和,公式为S=6a2, 已知正方体木块表面积,要求木块在桌面上所占面积,也就是求正方体其中一个面的面积,只需用正方体的表面积除以6即可。
【详解】72÷6=12(平方分米)
所以木块在桌面上所占的面积是12平方分米。
21. 12 6
【分析】由题意可知,铁丝的总长度就是正方体或者长方体的棱长总和,“棱长=正方体的棱长之和÷12”“高=长方体的棱长之和÷4-长-宽”,把题目中的数据代入公式计算,据此解答。
【详解】144÷12=12(厘米)
144÷4-20-10
=36-20-10
=6(厘米)
所以,正方体的棱长是12厘米,长方体的高是6厘米。
22.12.5
【分析】从题意可知:油箱里的油为长2.5分米,宽为2.5分米,高为2分米的长方体。根据长方体的体积(容积)=长×宽×高,代入数据计算即可。结果换算成升(1升=1立方分米)。
【详解】2.5×2.5×2=12.5(立方分米)
12.5立方分米=12.5升
这个油箱里有油12.5升。
23. 208cm2/208平方厘米 192cm3/192立方厘米
【分析】观察可知,长方体的长是8cm,宽是6cm,高是(cm),根据、,分别代入数据计算即可得解。
【详解】
(cm)
(cm2)
(cm3)
下图是一个长方体的表面展开图,这个长方体的表面积是208cm2,体积是192cm3。
24. 400 144 3600
【分析】长方体共有6个面,每个面都可能是底面,分别为前面、后面、左面、右面、上面和下面,其中前面和后面的面积相同,左面和右面的面积相同,上面和下面的面积相同,根据长方形的面积=长×宽,分别计算出前面、左面和上面的面积,再进行比较即可求出占地面积的最大值、最小值;
根据长方体的体积=长×宽×高,代入数据计算即可解答。
【详解】25×16=400(平方厘米)
25×9=225(平方厘米)
16×9=144(平方厘米)
400>225>144
25×16×9
=400×9
=3600(立方厘米)
所以它的占地面积最大是400平方厘米,最小是144平方厘米,体积是3600立方厘米。
25. 48 4
【分析】长方体框架的棱长总和就是这根铁丝的长,根据长方体的棱长总和=(长+宽+高)×4,代入数据计算即可求出这根铁丝的长;正方体的棱长总和=棱长×12,用这根铁丝的长除以12就是正方体的棱长。
【详解】(6+4+2)×4
=(10+2)×4
=12×4
=48(分米)
48÷12=4(分米)
所以这根铁丝长48分米,如果改做成一个正方体框架,棱长是4分米。
26.908
【分析】要想使打包得到的长方体表面积最小,就应使对接的全等的面的面积尽可能地大,因此首先两盒之间应以11×7的面对接,先组装成两个相同的长方体,其体积皆为11×7×(2×6)=11×7×12。由于12×7>11×7,因此这个组成的长方体对接面是12×7的两个面,如图
,根据长方体表面积=(长×宽+长×高+宽×高)×2,列式计算即可。
【详解】7+7=14(厘米)
(14×11+14×12+11×12)×2
=(154+168+132)×2
=454×2
=908(平方厘米)
按“规则方式”打包得到的长方体的表面积的最小值是908平方厘米。
27. 9 2
【分析】正方体展开图符合“2-2-2”型结构,折成正方体后,“1”对“5”,“2”对“4”,“3”对“6”,据此求出相对两个数的和与差,进而解答。
【详解】根据分析可知,折成正方体后,“1”对“5”,“2”对“4”,“3”对“6”。
1+5=6;5-1=4
2+4=6;4-2=2
3+6=9;6-3=3
和最大是9,差最小是2。
一个正方体的展开图,六个面上分别写有这六个数字,相对的两个面上数字的和最大是9,相对的两个面上数字的差最小是2。
28.爱
【分析】结合3种摆放情况可知,“南”对面不可能“小”,“活”、“狮”、“生”,所以“南”对面是“爱”,据此解答。
【详解】根据分析可知,一个正方体木块六个面上分别写上小、南、狮、爱、生、活这六个汉字。从不同角度看这个正方体,如图所示,通过推断可知“南”的对面是“爱”。
29. 64 32
【分析】根据题意可知:这个长方体盒子的侧面展开是一个边长8厘米的正方形,长方体的侧面积=底面周长×高,由此可知,这个长方体的底面周长和高都是8厘米,又已知底面是正方形,根摇正方形的周长公式:C=4a,那么a=C÷4,据此求出底面边长,然后根据长方体的体积公式:V=abh,把数据代入公式解答。
【详解】8×8=64(平方厘米)
8÷4=2(厘米)
2×2×8
=4×8
=32(立方厘米)
这个长方体的侧面积是64平方厘米,体积是32立方厘米。
30. 15 125 A B
【分析】根据题意可知,长方形的长和宽分别被正方体的边长平均分成4份和3份,那么长方形的长等于正方体边长的4倍,据此可求出正方体边长是5厘米,宽是边长的3倍,再根据V=a×a×a计算体积即可。折成正方体后D和A相对,C和E相对,B和F相对。再根据题中的摆放方式,找到右面的面是哪一面,据此解答。
【详解】20÷4×3
=5×3
=15(厘米)
5×5×5
=25×5
=125(立方厘米)
正方体展开图是2-3-1型,折成正方体后D和A相对,C和E相对,B和F相对。摆放如下图。
故长方形宽是15厘米,盒子体积是125立方厘米,和D面相对的是A面,如果D面是底面,从前面看是C面,那么右面是B面。
31. 20 60 74
【分析】观察图形可知,长方体玻璃容器的长可以摆5个,宽摆4个,根据长方形面积公式:面积=长×宽,据此求出一层可以摆小正方体的个数;
长方体容器的长摆5个,宽摆4个,高摆3个;根据长方体容积公式:容积=长×宽×高,代入数据,即可求出长方体容器可以摆小正方体的数量;
求做这个容器需要玻璃的面积,就是求长方体容器的5个面积的面积和;根据长方体5个面的表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,即可解答。
【详解】5×4=20(个)
5×4×3
=20×3
=60(个)
长:1×5=5(厘米);宽:1×4=4(厘米);高:1×3=3(厘米)
5×4+(5×3+4×3)×2
=20+(15+12)×2
=20+27×2
=20+54
=74(平方厘米)
在一个无盖的长方体玻璃容器内摆棱长为1厘米的小正方体,一层可以摆20个,一共可以摆60个,做这个容器需要玻璃74平方厘米。
32. 32 18
【分析】(1)观察可知,上下、左右各有5个小正方形,前后各有6个小正方形,根据,小正方体的每个面的面积是(平方厘米),用每个面的面积乘小正方形的总个数即可。
(2)观察可知,要搭一个大正方体,每条棱长最多有3个小正方体,即搭成的大正方体的棱长至少是3厘米,根据,代入数据可计算搭成的大正方体的体积及小正方体的体积,用大正方体体积除以小正方体体积,得到搭成的大正方体需要多少个小正方体,再减图中小正方体的个数即可得解。
【详解】
(平方厘米)
(个)
用棱长1厘米的小正方体搭成如图所示的图形,它的表面积是32平方厘米;至少再添加18个同样的小正方体,才能搭成一个大正方体。
33.10
【分析】根据正方体的体积公式:体积=棱长×棱长×棱长,代入数据,分别求出大正方体和小正方体的体积,再用大正方体的体积除以小正方体的体积,即可求出可以切成多少块小正方体,最后用小正方体的棱长×小正方体的个数,即可解答,注意单位名数的换算。
【详解】1厘米=0.01米
(1×1×1)÷(0.01×0.01×0.01)
=(1×1)÷(0.0001×0.01)
=1÷0.000001
=1000000(块)
0.01×1000000=10000(米)
10000米=10千米
把棱长1米的正方体切割成棱长1厘米的小正方体,把这些小正方体一个挨一个地连起来,可以排10千米。
34.2
【分析】正方体的特征:6个面都是正方形,且面积相等。正方体的展开图折成正方体时,相对的面不相邻。想象把正方体展开图折成正方体,取相对的面即可。
【详解】把正方体展开图折成一个正方体,可以想象成:3是下面,2是后面,1是左面,4是右面,5是上面,6是前面。
所以,这个正方体的6号面的对面是2号面。
35. ② ④
【分析】分析题目,根据正方形的面积=边长×边长可知小正方体每个面的面积是1×1=1(dm2),剩下部分图形的表面积比原来的大长方体的表面积增加4dm2,就是增加了4÷1=4(个)小正方形的面,据图可知,拿掉①或⑤表面积不变,拿掉②、③或④表面积都会增加2个面,拿掉中间相邻的两个②③或③④表面积会增加2个小正方形,拿掉中间不相邻的两个②和④表面积会增加4个小正方形,所以表面积想增加4dm2,得拿中间的,并隔一个拿一个,据此解答。
【详解】1×1=1(dm2)
4÷1=4(个)
根据分析,使所剩部分的表面积比原来长方体的表面积增加4dm2,拿②和④。
淘气用棱长1dm的小正方体拼成一个长方体。他要从5个有编号的小正方体中拿掉2个,使剩下图形的表面积比原来图形的表面积增加4dm2,他拿掉的小正方体编号可能是②和④。
36. 60 40
【分析】把一个长方体切开后,表面积会增加切面面积的两倍,要求表面积最多增加多少,说明切的那个面的面积必须最大;要求表面积最少增加多少,说明切的那个面的面积必须最小,由此找出长方体中最大面和最小面的面积,即可解答本题。
【详解】最大:(平方厘米)
最小:(平方厘米)
表面积最多可以增加60平方厘米,最少可以增加40平方厘米。
【点睛】本题考查了长方体切割后的图形的表面积计算,沿平行于宽高面切割,可使两个长方体的表面积之和最小;沿平行于长宽面切割,可使两个长方体的表面积之和最大。
37.160
【分析】通过观察图形可知,把2个棱长4分米的正方体拼成一个长方体,拼成的长方体的表面积比两个正方体的表面积和减少了正方体的2个面的面积(即重叠在一起的两个面),根据正方体的表面积公式:,把数据代入公式解答。
【详解】
(平方分米)
故拼成的长方体的表面积是160平方分米。
38.5
【分析】根据“正方体体积表示棱长)”计算出棱长是10厘米的正方体容器装满水后水的体积。注意水的体积不发生改变,再根据“长方体体积表示底面的长,表示底面的宽,表示高)”,即用正方体容器水的体积除以长方体底面积即可求出长方体水深。
【详解】
(厘米)
则此时长方体容器水深5厘米。
39.288
【分析】根据题意可知,增加的表面积等于4个长等于长方体的宽,宽等于长方体的高的长方形,用增加的面积÷4,求出一个面的面积,也就是长方体的底面积,再根据长方体体积公式:体积=底面积×高,代入数据,即可解答,注意单位名数的统一。
【详解】2.4m=24dm
48÷4×24
=12×24
=288(dm3)
原来长方体木料的体积是288dm3。
40. 158 52
【分析】长方体表面积(长宽长高宽高),代入数据计算即可解答第一个空;如果高减少2分米,即减少了长是8分米、宽是2分米的2个长方形的面积与长是5分米、宽是2分米的2个长方形的面积和,据此解答第二个空。
【详解】
(平方分米)
(平方厘米)
所以,一个长方体长8分米,宽5分米,高3分米,它的表面积是158平方分米,如果高减少2分米,表面积减少52平方分米。
41.0.006
【分析】根据切割方法,锯成两段时,表面积增加了2个横截面的面积,据此即可求出横截面的面积是(平方厘米),再根据长方体体积底面积高,用长方体木料的底面积乘木料的长,即可求出它的体积。
【详解】(平方厘米)
20平方厘米(平方米)
(立方米)
这根木料的体积是0.006立方米。
【点睛】解答此题的关键是根据切割方法,求出长方体木料的横截面的面积。要注意单位的统一。
42.55.5
【分析】沿着长、宽、高垂直各切一刀,表面一共增加了6个面,正好等于原来的表面积,据此分析。
【详解】沿着长、宽、高垂直各切一刀,增加上下、左右、前后6个面的面积,也就是原长方体的表面积。所以表面积比原来增加了55.5平方厘米。
43.22
【分析】根据正方体的表面积棱长棱长6,长方体的表面积(长宽长高宽高),把数据代入公式求出12个正方体的表面积和与长方体的表面积差即可。
【详解】按照图示拼成的长方体的长是12cm,宽和高都是1cm。
(cm2)
则表面积减少了22cm2。
44.
【分析】有大、中、小三个正方形的水池,可知这三个水池底面都是正方形的,把两堆沙分别沉没在中、小水池的水里,可知底面是不变的,只是水面会升高,升高那部分水的体积就是所放沙的体积,利用长方体的体积公式长宽高,求出两堆沙的体积;再将这两堆沙石都倒入大水池的水里,底面变了,体积没变,水面升高的那部分水的体积就是两堆沙的体积,再用两堆沙的体积和除以大正方形水池的底面积,即可解答,注意单位名数的统一。
【详解】2米=200厘米
3米=300厘米
6米=600厘米
200×200×4
=40000×4
=160000(立方厘米)
300×300×6
=90000×6
=540000(立方厘米)
(160000+540000)÷(600×600)
=700000÷360000
=(厘米)
如果把两堆沙都倒入大号水池,大号水池水面上升厘米。
45. 44 16
【分析】小正方体的每个面都是正方形,根据,可求出每个面的面积,观察可知, 这个图形从正面和后面看都有8个面,从上面和下面看都有6个面,从左面和右面看都有8个面,用每个面的面积乘面的总数可得这个图形的表面积。
观察可知这个图形一共有16个小正方体,根据,代入数据计算小正方体的体积,再用小正方体的体积乘16,即可得这个图形的体积。
【详解】
(平方厘米)
(立方厘米)
用棱长为1厘米的小正方体拼成下面的图形,这个图形的表面积是44平方厘米,体积是16立方厘米。
46. 15 46
【分析】根据正方体的体积公式V=a3,可知棱长1厘米的正方体的体积是1立方厘米;从图中数出正方体的个数,再乘用正方体的体积,即是这个几何体的体积。
已知正方体的棱长是1厘米,那么正方体一个面的面积是1平方厘米。求这个几何体的表面积,就是求露出正方体的面的面积之和,分别数出从上下面、前后面、左右面看到的小正方形的个数,再乘一个面的面积即可。
【详解】1×1×1×15=15(立方厘米)
(9+7+7)×2
=23×2
=46(个)
1×1×46=46(平方厘米)
它的体积是15立方厘米,表面积是46平方厘米。
47. 22 46
【分析】通过观察图形可知,需要胶带的长度等于这个包装箱的2条长加上2条宽再加上4条高的长度,根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式求出需要硬纸板的面积。
【详解】4×2+2×2+2.5×4
=8+4+10
=12+10
=22(分米)
(4×2+4×2.5+2×2.5)×2
=(8+10+5)×2
=23×2
=46(平方分米)
至少需要胶带22分米,做这个包装箱至少需要硬纸板46平方分米。
48.9
【分析】根据题意可知,把这个长方体木料横截成3段,表面积比原来增加了4个截面的面积,据此可以求出一个截面的面积,再根据长方体的体积公式:V=Sh,把数据代入公式解答。
【详解】1.5米=15分米
2.4÷4×15
=0.6×15
=9(立方分米)
原来这根木料的体积9立方分米。
49. 700 1000
【分析】看图可知,正方形纸板的边长包含2条高和2条宽,宽是高的2倍,根据和倍问题的解题方法,正方形边长÷(1+1+2+2)=高,高×2=宽,正方形边长-高×2=长,据此确定长方体的长、宽、高。根据长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,列式计算即可。
【详解】高:30÷(1+1+2+2)
=30÷6
=5(厘米)
宽:5×2=10(厘米)
长:30-5×2
=30-10
=20(厘米)
表面积:(20×10+20×5+10×5)×2
=(200+100+50)×2
=350×2
=700(平方厘米)
体积:20×10×5=1000(立方厘米)
它的表面积是700平方厘米,体积是1000立方厘米。
【点睛】关键是掌握和倍问题的解题方法,先确定长、宽、高,再灵活运用长方体表面积和体积公式。
50. 96 3.76 480
【分析】求铁丝的长其实就是求长方体的棱长总和,根据长方体的棱长总和=(长+宽+高)×4,代入数据计算即可。求彩纸的面积就是求长方体的表面积,根据,代入数据计算即可。再根据,计算可得长方体所占的空间。单位不同要统一单位。
【详解】
(厘米)
(平方厘米)
(平方分米)
(立方厘米)
用铁丝围成一个长方体框架,长10厘米,宽8厘米,高6厘米,铁丝长96厘米;如果给它各个面蒙上彩纸,至少要3.76平方分米的彩纸;这个长方体所占的空间是480立方厘米。
51.18
【分析】底面是正方形的长方体,侧面展开是周长16分米的正方形,由此可知,周长16分米的正方形的边长等于底面正方形的周长、等于原长方体的高,由正方形的周长=边长×4,用16÷4求出原长方体的高,再用原长方体的高除以4求出底面正方形的边长,该长方体的表面积=侧面积+底面正方形面积的2倍,侧面积=边长是16÷4=4(分米)的正方形的面积,根据正方形的面积=边长×边长解答。
【详解】16÷4÷4
=4÷4
=1(分米)
1×1×2+(16÷4)×(16÷4)
=2+4×4
=2+16
=18(平方分米)
所以它的表面积是18平方分米。
52.200
【分析】根据题意,把长方体木料锯成4段,要截3次;每截一次增加2个截面,截3次增加6个截面,表面积会增加6个截面的面积;
先用增加的表面积除以6,求出一个截面的面积;再根据长方体的体积公式V=Sh,求出原来木料的体积。注意单位的换算:1米=10分米。
【详解】2.5米=25分米
增加截面的个数:
(4-1)×2
=3×2
=6(个)
截面的面积:48÷6=8(平方分米)
体积:8×25=200(立方分米)
原来这根木料的体积是200立方分米。
53.5
【分析】根据题意,作图如下:
从“一个长方体,如果高增加3厘米,就变成一个正方体”可知:这个长方体的高+3厘米=长=宽=正方体的棱长。高增加3厘米,就从长方体变成正方体,上下面不变,前后左右4个面共增加了96平方厘米,用96÷4=24平方厘米求出一个面增加的面积。再用一个面增加的面积÷3即可得正方体的棱长,用棱长减去3就得长方体的高。
【详解】96÷4÷3-3
=8-3
=5(厘米)
原来长方体的高是5厘米。
54.16
【分析】根据题意,结合正方体的体积公式:边长×边长×边长,先求出正方体的边长,再结合底面积=边长×边长,代入数据计算即可。
【详解】64=4×4×4
4×4=16(平方分米)
所以它的底面积是16平方分米。
55.85
【分析】求鱼缸玻璃和水的接触面积,实际上就是求由水组成的长5分米、宽5分米、高3分米的长方体的5个面的面积,再结合长方体表面积的计算公式即可求解。
【详解】(5×3+5×3)×2+5×5
=(15+15)×2+5×5
=30×2+5×5
=60+25
=85(平方分米)
则与水接触的玻璃的面积是85平方分米。
56.4800
【分析】求铁皮的面积就是求长方体的侧面积,根据长方体的侧面积=底面周长×高,据此进行计算即可。
【详解】1.2米=120厘米
10×4×120
=40×120
=4800(平方厘米)
则至少需要铁皮4800平方厘米。
57. 4 20
【分析】求蓄水箱的占地面积就是求边长为2米的正方形的面积,根据正方形的面积=边长×边长,据此计算即可;求无盖正方体蓄水箱需要的铁皮就是求正方体五个面的面积,根据正方体五个面的面积=一个面的面积×5,据此进行计算即可。
【详解】2×2=4(平方米)
2×2×5
=4×5
=20(平方米)
则它的占地面积是4平方米,制作一个至少需要20平方米铁皮。
58.2ab
【分析】根据题意,一个长为a米、宽为b米的长方体的高增加2米,那么增加的体积就是高为2米的长方体的体积,根据长方体的体积=长×宽×高,即可求出比原来增加的体积。
【详解】a×b×2=2ab(立方米)
体积比原来增加2ab立方米。
59. 1000000 9
【分析】先根据正方体的体积公式V=a3,求出棱长为1m和棱长为1cm的大、小正方体的体积,再用大正方体的体积除以小正方体的体积,即是一共能切成小正方体的块数;
把棱长1cm的小正方体木块排成一排,用小正方体的棱长乘小正方体的块数,求出排成一排的距离,再减去1km即可。
注意单位的换算:1m=100cm,1km=100000cm。
【详解】1m=100cm
(100×100×100)÷(1×1×1)
=1000000÷1
=1000000(块)
1000000×1=1000000(cm)
1000000cm=10km
10-1=9(km)
一共能切(1000000)块,把它们排成一排,排成的距离比1km多(9)km。
60.8.064
【分析】要求这个水泥池的容积,需要知道水泥池里面的长、宽和高,所以先求出水泥池的长和宽,分别减去两个墙厚即可,高不变,然后用长方体容积公式:容积=长×宽×高,代入数据,就可求出体积,注意单位名数的统一。
【详解】10cm=0.1m
(3-0.1×2)×(2-0.1×2)×1.6
=(3-0.2)×(2-0.2)×1.6
=2.8×1.8×1.6
=5.04×1.6
=8.064(m3)
这个水池的容积是8.064m3。
答案第24页,共24页
答案第23页,共23页
