2.4.2等比数列的性质和应用 (第2课时)
文档属性
| 名称 | 2.4.2等比数列的性质和应用 (第2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-05 20:19:17 | ||
图片预览








文档简介
课件24张PPT。2.4.1等比数列的性质和应用
(第二课时) 高中数学教师欧阳文丰制作2.类比等差数列的性质,探究等比数列的性质: an+1-an=dd 叫公差 an= a1+(n-1)dq叫公比 an=a1qn-11.温故知新等差数列{ an }中 ,(m 、 n、p、q ∈ N+):① an=am+ (n-m)d
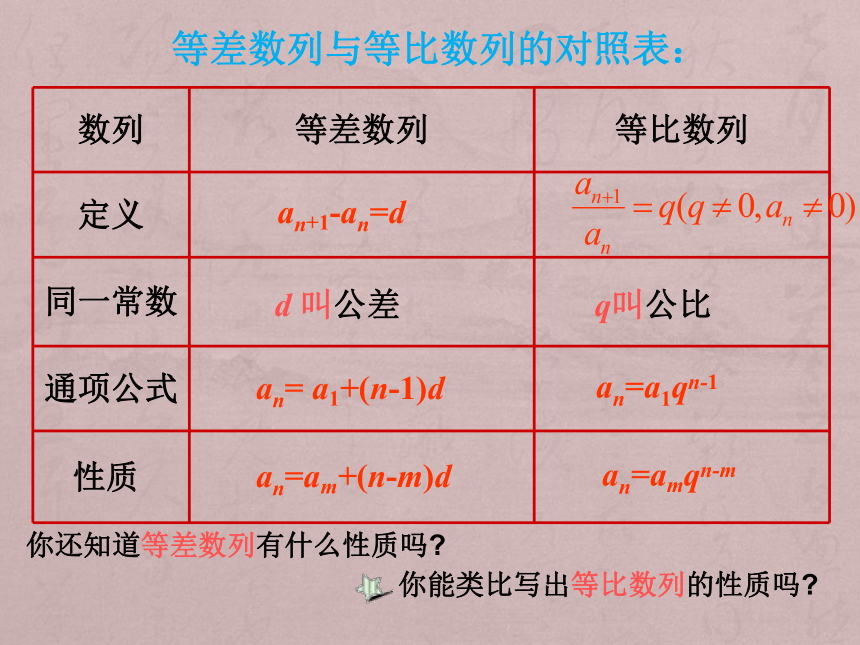
②若 m+n=p+q 则 am+an=ap+aq 一、例题探究等差数列与等比数列的对照表: an+1-an=dd 叫公差 an= a1+(n-1)d an=am+(n-m)d你还知道等差数列有什么性质吗?你能类比写出等比数列的性质吗?q叫公比 an=a1qn-1 an=amqn-m思考:我们知道,等差数列{an}满足下列公式
(1)an=am+(n-m)d;
(2)若m+n=p+q,则am+an =ap+aq
那么,等比数列是否也有类似的公式呢?在等比数列{an}中,
(1)an=amqn-m;
(2)若m+n=p+q,则am·an =ap·aq
特别地,若m+n=2p,则am·an =ap2 例2、已知{an},{bn}是项数相同的等比数列,那么数列
{anbn}还是等比数列吗?试证明你的观点。证明:设{an}的公比为p,{bn}的公比为q,则 ∵pq是一个与n无关的常数,
∴{anbn}是以pq为公比的等比数列.思考:那数列 是不是也是等比数列呢? {an+bn}呢?探究1:若{an} 是公比为q的等比数列,c为常数,则下列数列是等比数列吗?若是,公比是什么?探究2:若{an}是各项为正数的等比数列,则下面的
数列是等比数列吗?√√√×1或-2随堂练习一:1.在等比数列{an}中,若2an=an+1+an+2,则公比q=______.9±381C4.已知是等比数列,且an>0,a2a4+2a3a5+a4a6=25,
那么a3+a5= ( )
A.5 B.10 C.15 D.20
5.等比数列{an}中,a4+a6=3,则a5(a3+2a5+a7)=____A9随堂练习二:2.若lga,lgb,lgc成等差数列,则a,b,c成 数列;等比拓展:若 a,b,c成等比数列,则lga,lgb,lgc是否
一定成等差数列?不一定,只有当a,b,c都大于0才成立.1.若2a,2b,2c成等比数列,则a,b,c成 数列;等差 观察如下的两个数之间,插入一个什么数后这三个数就会成为一个等比数列:(1)1, , 9 (2)-1, ,-4
(3)-12, ,-3 (4)1, ,1±3±2±6±1 如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项。二、等比中项练习:已知等差数列{an}的公差d≠0,
且a1,a3,a9成等比数列,则 a1+a3+a9
的值为________.
a2+a4+a10易错点评:没有分清等差数列与等比数列.例3、已知三数成等比数列,它们的和等于14,它们的积是64,求这三个数.故这三个数为2,4,8或8,4,2. [变式练习] 有四个数,其中前三个数成等差数列,后三个数成等比数列,并且前后两数的和是16,中间两数的和是12.求这四个数.
易错点评:审题不细心.根据a7是a5与a9的等比中项求出a7 后易忽视对a7 符号的讨论.补充例题讲解归纳总结判断一个数列是等比数列常用的方法:等差数列与等比数列的类比(2)若m+n=p+q
(m,n,p,q∈N+)
则 am· an=ap· aq .(2)若m+n=p+q (m,n,p,q∈N+)
则 am+an=ap+aq .2an=an-1+ an+1 .(3) an2=an-1· an+1 .(1)证明:∵ a1=1>0
∴由an+1=2an+1可知{an}是递增数列
∴an>0,故an+1≠0∵an+1+1=2an+2=2(an+1)∴数列{an+1}是等比数列.思考:已知数列{an}满足a1=1,an+1=2an+1.
(1)求证数列{an+1}是等比数列;
(2)求数列{an}的通项公式.附加、构造新数列转化为等比数列求通项公式:(2)解:∵ a1=1
∴a1+1=2
∴数列{an+1}是一个首项为2,公比也为2
的等比数列
∴an+1=2×2n-1=2n
故an=2n-1思考:已知数列{an}满足a1=1,an+1=2an+1.
(1)求证数列{an+1}是等比数列;
(2)求数列{an}的通项公式.
(1)求a2,a3,并证明数列{an-n}是等比数列;
(2)求an.
[思路探索] (1)变形递推公式,按等比数列的定义证明;
(2)求出{an-n}的通项公式,即可求出an.
解 (1)a2=3a1-2×2+3=-4,
a3=3a2-2×3+3=-15.
下面证明{an-n}是等比数列:
【例5】 数列{an}满足a1=-1,且an=3an-1-2n+3(n=
2,3,…).
(第二课时) 高中数学教师欧阳文丰制作2.类比等差数列的性质,探究等比数列的性质: an+1-an=dd 叫公差 an= a1+(n-1)dq叫公比 an=a1qn-11.温故知新等差数列{ an }中 ,(m 、 n、p、q ∈ N+):① an=am+ (n-m)d
②若 m+n=p+q 则 am+an=ap+aq 一、例题探究等差数列与等比数列的对照表: an+1-an=dd 叫公差 an= a1+(n-1)d an=am+(n-m)d你还知道等差数列有什么性质吗?你能类比写出等比数列的性质吗?q叫公比 an=a1qn-1 an=amqn-m思考:我们知道,等差数列{an}满足下列公式
(1)an=am+(n-m)d;
(2)若m+n=p+q,则am+an =ap+aq
那么,等比数列是否也有类似的公式呢?在等比数列{an}中,
(1)an=amqn-m;
(2)若m+n=p+q,则am·an =ap·aq
特别地,若m+n=2p,则am·an =ap2 例2、已知{an},{bn}是项数相同的等比数列,那么数列
{anbn}还是等比数列吗?试证明你的观点。证明:设{an}的公比为p,{bn}的公比为q,则 ∵pq是一个与n无关的常数,
∴{anbn}是以pq为公比的等比数列.思考:那数列 是不是也是等比数列呢? {an+bn}呢?探究1:若{an} 是公比为q的等比数列,c为常数,则下列数列是等比数列吗?若是,公比是什么?探究2:若{an}是各项为正数的等比数列,则下面的
数列是等比数列吗?√√√×1或-2随堂练习一:1.在等比数列{an}中,若2an=an+1+an+2,则公比q=______.9±381C4.已知是等比数列,且an>0,a2a4+2a3a5+a4a6=25,
那么a3+a5= ( )
A.5 B.10 C.15 D.20
5.等比数列{an}中,a4+a6=3,则a5(a3+2a5+a7)=____A9随堂练习二:2.若lga,lgb,lgc成等差数列,则a,b,c成 数列;等比拓展:若 a,b,c成等比数列,则lga,lgb,lgc是否
一定成等差数列?不一定,只有当a,b,c都大于0才成立.1.若2a,2b,2c成等比数列,则a,b,c成 数列;等差 观察如下的两个数之间,插入一个什么数后这三个数就会成为一个等比数列:(1)1, , 9 (2)-1, ,-4
(3)-12, ,-3 (4)1, ,1±3±2±6±1 如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项。二、等比中项练习:已知等差数列{an}的公差d≠0,
且a1,a3,a9成等比数列,则 a1+a3+a9
的值为________.
a2+a4+a10易错点评:没有分清等差数列与等比数列.例3、已知三数成等比数列,它们的和等于14,它们的积是64,求这三个数.故这三个数为2,4,8或8,4,2. [变式练习] 有四个数,其中前三个数成等差数列,后三个数成等比数列,并且前后两数的和是16,中间两数的和是12.求这四个数.
易错点评:审题不细心.根据a7是a5与a9的等比中项求出a7 后易忽视对a7 符号的讨论.补充例题讲解归纳总结判断一个数列是等比数列常用的方法:等差数列与等比数列的类比(2)若m+n=p+q
(m,n,p,q∈N+)
则 am· an=ap· aq .(2)若m+n=p+q (m,n,p,q∈N+)
则 am+an=ap+aq .2an=an-1+ an+1 .(3) an2=an-1· an+1 .(1)证明:∵ a1=1>0
∴由an+1=2an+1可知{an}是递增数列
∴an>0,故an+1≠0∵an+1+1=2an+2=2(an+1)∴数列{an+1}是等比数列.思考:已知数列{an}满足a1=1,an+1=2an+1.
(1)求证数列{an+1}是等比数列;
(2)求数列{an}的通项公式.附加、构造新数列转化为等比数列求通项公式:(2)解:∵ a1=1
∴a1+1=2
∴数列{an+1}是一个首项为2,公比也为2
的等比数列
∴an+1=2×2n-1=2n
故an=2n-1思考:已知数列{an}满足a1=1,an+1=2an+1.
(1)求证数列{an+1}是等比数列;
(2)求数列{an}的通项公式.
(1)求a2,a3,并证明数列{an-n}是等比数列;
(2)求an.
[思路探索] (1)变形递推公式,按等比数列的定义证明;
(2)求出{an-n}的通项公式,即可求出an.
解 (1)a2=3a1-2×2+3=-4,
a3=3a2-2×3+3=-15.
下面证明{an-n}是等比数列:
【例5】 数列{an}满足a1=-1,且an=3an-1-2n+3(n=
2,3,…).
