人教版九年级数学下册:28.2 解直角三角形的应用教学课件 (共13张PPT)
文档属性
| 名称 | 人教版九年级数学下册:28.2 解直角三角形的应用教学课件 (共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 652.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-07 14:20:01 | ||
图片预览



文档简介
课件13张PPT。28.2解直角三角形的应用解直角
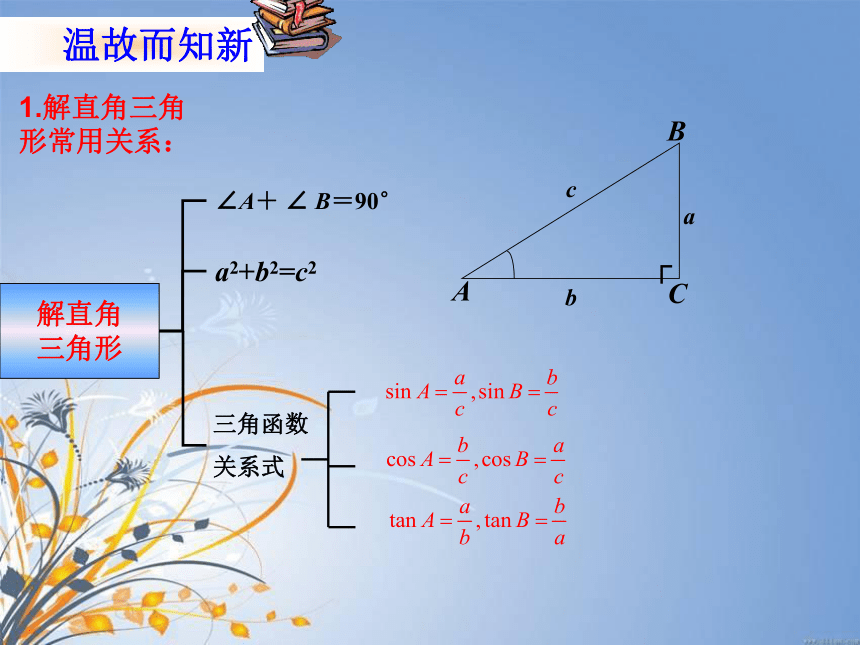
三角形∠A+ ∠ B=90°a2+b2=c2三角函数
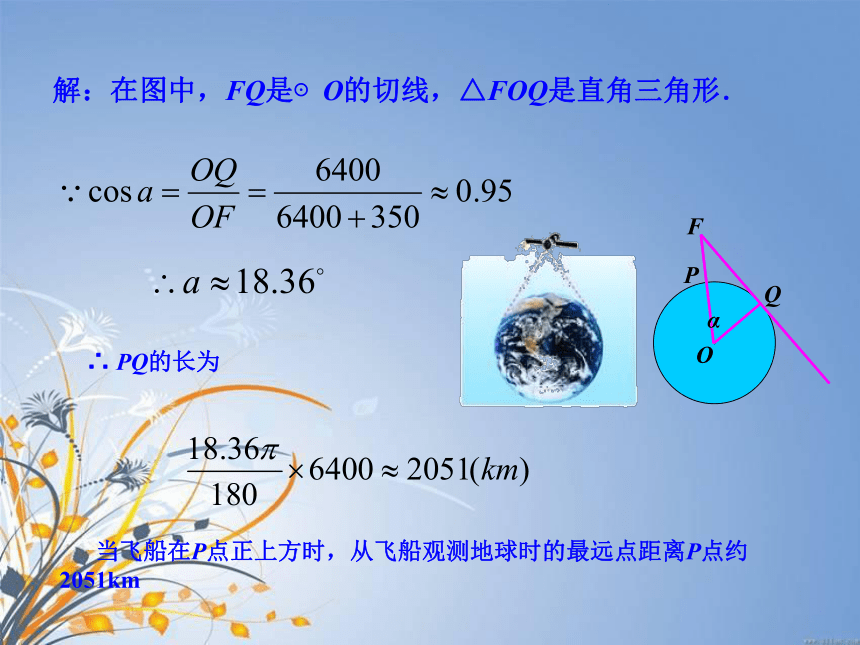
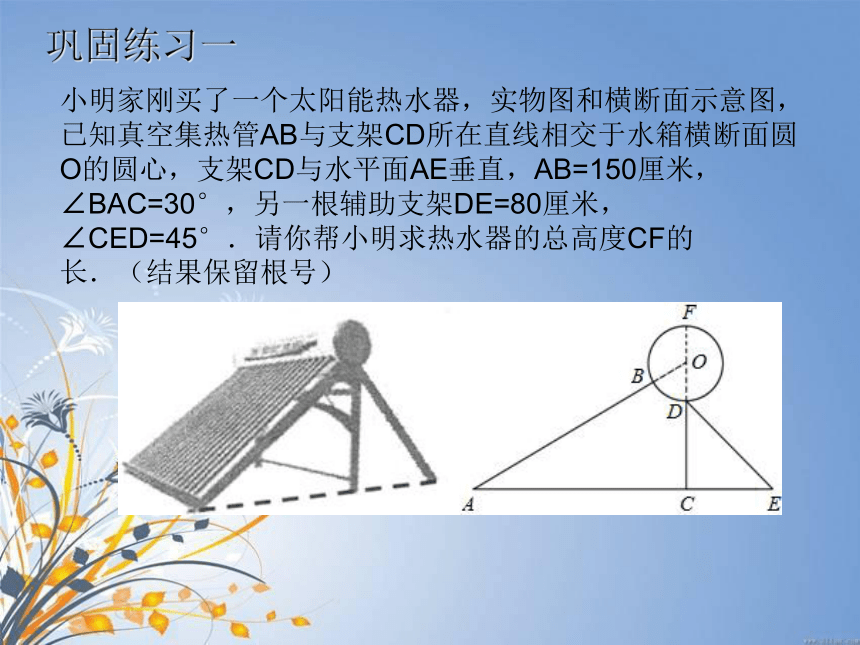
关系式1.解直角三角形常用关系:2.如图,Rt△ABC中,∠C=90°,已知a=2√3,c=4,求∠B应该用哪个关系?请计算出来。例3: 2003年10月15日“神舟”5号载人航天飞船发射成功.当飞船完成变轨后,就在离地球表面350km的圆形轨道上运行.如图,当飞船运行到地球表面上P点的正上方时,从飞船上最远能直接看到地球上的点在什么位置?这样的最远点与P点的距离是多少?(地球半径约为6 400km,结果取整数) 分析:从飞船上能最远直接看到的地球上的点,应是视线与地球相切时的切点.测量中的最远点问题解:在图中,FQ是⊙O的切线,△FOQ是直角三角形.∴ PQ的长为 当飞船在P点正上方时,从飞船观测地球时的最远点距离P点约2051km小明家刚买了一个太阳能热水器,实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面圆O的圆心,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=80厘米,∠CED=45°.请你帮小明求热水器的总高度CF的长.(结果保留根号)
巩固练习一读一读在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
仰角和俯角例4: 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m)分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60° Rt△ABC中,a =30°,AD=120,
所以利用解直角三角形的知识求出
BD;类似地可以求出CD,进而求出BC.仰角与俯角解:如图,a = 30°,β= 60°, AD=120.答:这栋楼高约为277.1mA巩固练习二 太子灵踪塔是我县标志性建筑之一.如图,在一次数学课外实践活动中,老师要求测塔的高度AB.小明在D处用高1.5m的测角仪CD,测得塔顶端A的仰角为30°,然后向塔前进224m到达E处,又测得塔顶端A的仰角为60°.求太子灵踪塔的高度AB.(结果保留根号)1.如图1,在离铁塔BE 120m的A处,用测角仪测量塔顶的仰角为30°,已知测角仪高AD=1.5m,则塔高BE= _________ (根号保留).图12.如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶部A点测建筑物CD的顶部C点的俯角∠EAC为30度.测得建筑物CD的底部D点的俯角∠EAD为45度.
(1)求两建筑物底部之间水平距离BD的长度; (2)求建筑物CD的高度(结果保留根号). 1.数形结合思想.方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.课堂小结2.方程思想.3.转化(化归)思想.小刘想测量学校操场旗杆顶端到地面的距离,但旗杆底部不能直接到达,请你应用今天所学知识,帮助他设计一个测量方案,画出示意图,相关数据用字母表示,并与同学交流。作业布置
三角形∠A+ ∠ B=90°a2+b2=c2三角函数
关系式1.解直角三角形常用关系:2.如图,Rt△ABC中,∠C=90°,已知a=2√3,c=4,求∠B应该用哪个关系?请计算出来。例3: 2003年10月15日“神舟”5号载人航天飞船发射成功.当飞船完成变轨后,就在离地球表面350km的圆形轨道上运行.如图,当飞船运行到地球表面上P点的正上方时,从飞船上最远能直接看到地球上的点在什么位置?这样的最远点与P点的距离是多少?(地球半径约为6 400km,结果取整数) 分析:从飞船上能最远直接看到的地球上的点,应是视线与地球相切时的切点.测量中的最远点问题解:在图中,FQ是⊙O的切线,△FOQ是直角三角形.∴ PQ的长为 当飞船在P点正上方时,从飞船观测地球时的最远点距离P点约2051km小明家刚买了一个太阳能热水器,实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面圆O的圆心,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=80厘米,∠CED=45°.请你帮小明求热水器的总高度CF的长.(结果保留根号)
巩固练习一读一读在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
仰角和俯角例4: 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m)分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60° Rt△ABC中,a =30°,AD=120,
所以利用解直角三角形的知识求出
BD;类似地可以求出CD,进而求出BC.仰角与俯角解:如图,a = 30°,β= 60°, AD=120.答:这栋楼高约为277.1mA巩固练习二 太子灵踪塔是我县标志性建筑之一.如图,在一次数学课外实践活动中,老师要求测塔的高度AB.小明在D处用高1.5m的测角仪CD,测得塔顶端A的仰角为30°,然后向塔前进224m到达E处,又测得塔顶端A的仰角为60°.求太子灵踪塔的高度AB.(结果保留根号)1.如图1,在离铁塔BE 120m的A处,用测角仪测量塔顶的仰角为30°,已知测角仪高AD=1.5m,则塔高BE= _________ (根号保留).图12.如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶部A点测建筑物CD的顶部C点的俯角∠EAC为30度.测得建筑物CD的底部D点的俯角∠EAD为45度.
(1)求两建筑物底部之间水平距离BD的长度; (2)求建筑物CD的高度(结果保留根号). 1.数形结合思想.方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.课堂小结2.方程思想.3.转化(化归)思想.小刘想测量学校操场旗杆顶端到地面的距离,但旗杆底部不能直接到达,请你应用今天所学知识,帮助他设计一个测量方案,画出示意图,相关数据用字母表示,并与同学交流。作业布置
