山东省鄄城县第一中学2016年高一探究部自主招生考试数学试题
文档属性
| 名称 | 山东省鄄城县第一中学2016年高一探究部自主招生考试数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 235.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-06 00:00:00 | ||
图片预览



文档简介
初三数学试题
本试卷分两部分,第一部分为选择题和填空题,第二部分为解答题,共6页.满分100分,考试用时100分钟.考试结束后,只将答题卡交回.
第一部分(选择题和填空题,共42分)
一、选择题:(本大题共8个小题,在每小题的四个选项中只有一个是正确的,请把正确的选项选出来,用2B铅笔把答题卡上对应题目的答案标号涂黑.每小题涂对得3分,满分24分.)
1.下列运算正确的是(
)
2.在算式的中填上运算符号,使结果最大,这个运算符号是( )
A. 加号
B. 减号
C. 乘号
D. 除号
3.用配方法解一元二次方程时,下列变形正确的为(
)
A.
B.
C.
D.
4.如图,一次函数y=kx+b的图像经过A、B两点,则kx+b>2的解集是(
)
A.x<-3
B.x>-3
C.x<0
D.x>0
4题图
5题图
5.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,
某女士身高165cm,下半身长x与身高l的比值是0.58,为尽可能达到美的效果,她应穿
的高跟鞋的高度大约为( )
A.4cm
B.6cm
C.8cm
D.10cm
6.如图,菱形ABCD中,∠B=60°,AB=4cm,
E、F分别是
BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )
A.4cm
B.6cm
C.8cm
D.6cm
(6题图)
一枚均匀的正方体骰子,六个面分别标有数字1,2,3,4,5,6,连续抛掷两次,朝上
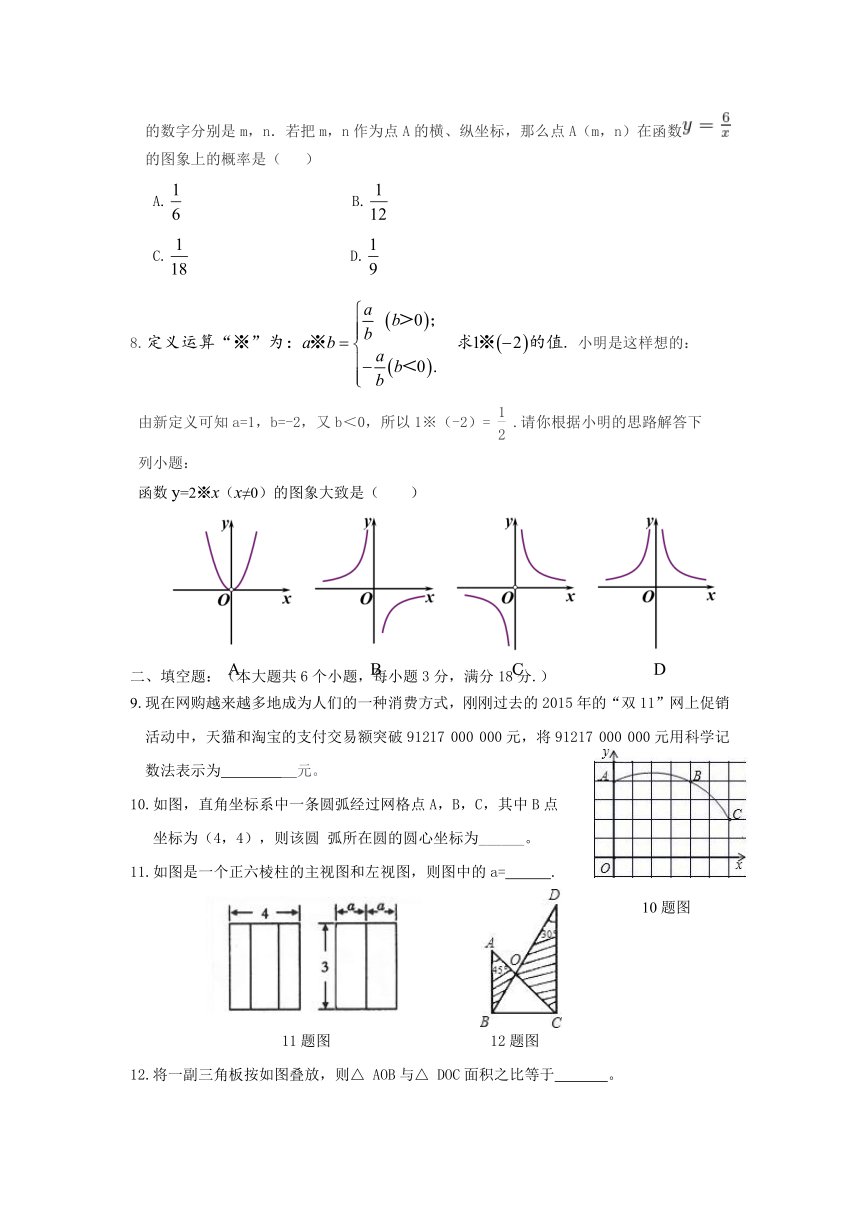
的数字分别是m,n.若把m,n作为点A的横、纵坐标,那么点A(m,n)在函数
的图象上的概率是(
)
A.
B.
C.
D.
小明是这样想的:
由新定义可知a=1,b=-2,又b<0,所以1※(-2)=
.请你根据小明的思路解答下
列小题:
函数y=2※x(x≠0)的图象大致是( )
二、填空题:(本大题共6个小题,每小题3分,满分18分.)
9.现在网购越来越多地成为人们的一种消费方式,刚刚过去的2015年的“双11”网上促销
活动中,天猫和淘宝的支付交易额突破91217
000
000元,将91217
000
000元用科学记
数法表示为 元。
如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点
坐标为(4,4),则该圆
弧所在圆的圆心坐标为______。
如图是一个正六棱柱的主视图和左视图,则图中的a= .
11题图
12题图
12.将一副三角板按如图叠放,则△
AOB与△
DOC面积之比等于
。
13.如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在点A′的位置上,若OA=1,tan∠BOC=,则点A′的坐标为________.
13题图
14题图
如图,抛物线y=ax2+bx+c的对称轴是x=-1,且过点(),有下列结论:①abc>0;
②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0;⑤a-b≥m(am-b);其中所有正确的结
论是________(填写正确结论的序号).
三、解答题:本大题共6个小题,满分58分.
解答时请写出必要的演推过程.
15.(每小题5分
共10分)
(1)计算:
(2)解方程:
16.(每小题5分
共10分)
(1)如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,
点E在BC边上,且BE=BD,连结AE、DE、DC.
16(1)题图
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
某居民小区为缓解居民停车难问题为缓解“停车难”问题,拟造地下停车库,如图是地
下停车库
坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C
在
BD
上,
BC=0.5.根据规定,地下停
车库破道口上方要张贴限高标志,以便告知驾驶员所驾
车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的
长作为限制的高度。小明和小亮谁说的对?请你判断并计算出正确的结果。
(sin18°≈0.309,cos18°≈0.951,tan18°≈0.325,结果精确到
0.1
米)
16(2)题图
17(1)题图
17.(本小题满分10分
每小题5分)
(1)如图,直线y
=2x+
3与x轴相交于点A,与y轴相交于点B.
①求A,B两点的坐标;
②过B点作直线BP与x轴的正半轴相交于P,且使OP
=
2OA,求ΔABP的面积.
(2)如图,在△AOB中,OA=OB,∠A=30 ,⊙O经过AB的中点E分别交OA、OB于C、D两点,连接CD.
(1)求证:AB是⊙O的切线.
(2)求证:AB∥CD.
(3)若CD=4,求扇形OCED的面积.
18.(本题满分8分)
17(2)题图
初中生对待学习的态度一直是教育工作者关注的问题之一.为此菏泽市教育局对我市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了__________名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
(第18题图)
19.(本题满分10分)我市为绿化城区,计划购买甲、乙两种树苗共计500棵,甲种树苗每棵50元,乙种树苗每棵80元,调查统计得:甲、乙两种树苗的成活率分别为90%、95%.
(1)如果购买两种树苗共用28000元,那么甲、乙两种树苗各买了多少棵?
(2)市绿化部门研究决定,购买树苗的钱数不得超过34000元,应如何选购树苗?
(3)要使这批树苗的成活率不低于92%,且使购买树苗的费用最低,应如何选购树苗?最低费用是多少?
20.(10分)
如图(1),矩形ABCD的一边BC在直角坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(m,0),其中m>0。
(1)求点E、F的坐标(用含m的式子表示);
(2)连接OA,若△OAF是等腰三角形,求m的值;
(3)如图(2),设抛物线y=a(x-m-6)2+h经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值。
第20题图
初三数学试题参考答案
第Ⅰ卷(选择题,共24分)
一、选择题:本大题共8个小题,每小题涂对得3分,满分24分.
题号
1
2
3
4
5
6
7
8
答案
D
D
B
D
C
B
D
D
第Ⅱ卷(非选择题,共76分)
填空题:本大题共6个小题,每小题3分,满分18分.
9.
9.1217X1010
10.
(2,0)
11.
12.
1:3
13.
14.①③⑤
三、解答题:
15(1)
(2)2=2x-1-3
2x=6
x=3
经检验,x=3是原分式方程的解.
16.(1)①证明:∵∠ABC=90°,D为AB延长线上一点,
∴∠ABE=∠CBD=90°,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS);
②解:∵AB=CB,∠ABC=90°,
∴∠CAB=45°,
∵∠CAE=30°,
∴∠BAE=∠CAB﹣∠CAE=45°﹣30°=15°,
∵△ABE≌△CBD,
∴∠BCD=∠BAE=15°,
∴∠BDC=90°﹣∠BCD=90°﹣15°=75°;
(2)解:∵AB⊥BD,
∴∠ABD=90°,
∴BD=AB tan∠BAD=10×tan18°=3.2(m),
∴CD=BD﹣BC=3.2﹣0.5=2.7(m),
∵∠BAD+∠BDA=∠DCE+∠BDA=90°,
∴∠DCE=18°,
∴CE=CD sin∠BDE=2.7×sin18°=2.7×0.95≈2.6(m),
即该地下停车库限高
CE
的长约为
2.6m.
17.解:(1)①∵y=2x+3,
∴当y=0时,x=-;当x=0时,y=3,
∴A(-,0)
B(0,3);
②∵OP=2OA=3,
∴AP=AO+OP=+3=
∴S△ABP=×AP×OB=××3=.
∴S△ABP=。
(2)证明:(1)证明:连接
4分
(2)证明:在
8分
(3)解:,,
12分
18.解:(1)50÷25%=200;(2分)
(2)200-120-50=30(人).画图如下.
(5分)
(3)C所占圆心角度数=360°×(1-25%-60%)=54°.(8分)
(4)80000×(25%+60%)=68000,
∴估计该市初中生中大约有68000名学生学习态度达标.(10分)
19.
设购买甲种树苗x棵,则购买乙种树苗为(500-x)棵,由题意得
50x+80(500-x)=28000.
解得x=400.
所以500-x=100.
答:购买甲种树苗400棵,购买乙种树苗100棵.
4分
(2)由题意得:
解得,(注意
答:购买甲种树苗不少于200棵,其余购买乙种树苗.
8分
(注意:得到购买乙种树苗不多于300棵,其余购买甲种树苗……也对)
(3)由题意得
设购买两种树苗的费用之和为y,
则
在此函数中,y随x的增大而减小,
所以当时,取得最小值,其最小值为
答:购买甲种树苗300棵,购买乙种树苗200棵,即可满足这批树苗的成活率不低于92%,又使购买树苗的费用最低,其最低费用为31000元.
12分
20.解:(1)∵四边形ABCD是矩形,
∴AD=BC=10,AB=CD=8,∠D=∠DCB=∠ABC=90°
由折叠对称性:AF=AD=10,FE=DE
在Rt△ABF中,BF=
∴FC=4
设FE=DE=x,
在Rt△ECF中,42+(8-x)2=x2,
解得x=5,CE=8-x=3
∵B(m,0),
∴E(m+10,3),F(m+6,0)。
(2)分三种情形讨论:
若AO=AF,
∵AB⊥OF,
∴OB=BF=6,
∴m=6
若FO=FA,则m+6=10,解得m=4
若OA=OF,在Rt△AOB中,
∴,解得m=
综上所述:m=6或4或。
(3)由(1)知A(m,8),E(m+10,3),
由题意得
解得
∴M(m+6,-1)
设抛物线的对称轴交AD于G
∴G(m+6,8),
∴AG=6,GM=9
∵∠OAB+∠BAM=90°,∠BAM+∠MAG=90°,
∴∠OAB=∠MAG
又∵∠ABO=∠MGA=90°,
∴△AOB∽△AMG
∴
即
∴m=12。
A
B
D
E
C
F
A
B
C
D
10题图
A
E
B
O
C
D
本试卷分两部分,第一部分为选择题和填空题,第二部分为解答题,共6页.满分100分,考试用时100分钟.考试结束后,只将答题卡交回.
第一部分(选择题和填空题,共42分)
一、选择题:(本大题共8个小题,在每小题的四个选项中只有一个是正确的,请把正确的选项选出来,用2B铅笔把答题卡上对应题目的答案标号涂黑.每小题涂对得3分,满分24分.)
1.下列运算正确的是(
)
2.在算式的中填上运算符号,使结果最大,这个运算符号是( )
A. 加号
B. 减号
C. 乘号
D. 除号
3.用配方法解一元二次方程时,下列变形正确的为(
)
A.
B.
C.
D.
4.如图,一次函数y=kx+b的图像经过A、B两点,则kx+b>2的解集是(
)
A.x<-3
B.x>-3
C.x<0
D.x>0
4题图
5题图
5.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,
某女士身高165cm,下半身长x与身高l的比值是0.58,为尽可能达到美的效果,她应穿
的高跟鞋的高度大约为( )
A.4cm
B.6cm
C.8cm
D.10cm
6.如图,菱形ABCD中,∠B=60°,AB=4cm,
E、F分别是
BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )
A.4cm
B.6cm
C.8cm
D.6cm
(6题图)
一枚均匀的正方体骰子,六个面分别标有数字1,2,3,4,5,6,连续抛掷两次,朝上
的数字分别是m,n.若把m,n作为点A的横、纵坐标,那么点A(m,n)在函数
的图象上的概率是(
)
A.
B.
C.
D.
小明是这样想的:
由新定义可知a=1,b=-2,又b<0,所以1※(-2)=
.请你根据小明的思路解答下
列小题:
函数y=2※x(x≠0)的图象大致是( )
二、填空题:(本大题共6个小题,每小题3分,满分18分.)
9.现在网购越来越多地成为人们的一种消费方式,刚刚过去的2015年的“双11”网上促销
活动中,天猫和淘宝的支付交易额突破91217
000
000元,将91217
000
000元用科学记
数法表示为 元。
如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点
坐标为(4,4),则该圆
弧所在圆的圆心坐标为______。
如图是一个正六棱柱的主视图和左视图,则图中的a= .
11题图
12题图
12.将一副三角板按如图叠放,则△
AOB与△
DOC面积之比等于
。
13.如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在点A′的位置上,若OA=1,tan∠BOC=,则点A′的坐标为________.
13题图
14题图
如图,抛物线y=ax2+bx+c的对称轴是x=-1,且过点(),有下列结论:①abc>0;
②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0;⑤a-b≥m(am-b);其中所有正确的结
论是________(填写正确结论的序号).
三、解答题:本大题共6个小题,满分58分.
解答时请写出必要的演推过程.
15.(每小题5分
共10分)
(1)计算:
(2)解方程:
16.(每小题5分
共10分)
(1)如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,
点E在BC边上,且BE=BD,连结AE、DE、DC.
16(1)题图
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
某居民小区为缓解居民停车难问题为缓解“停车难”问题,拟造地下停车库,如图是地
下停车库
坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C
在
BD
上,
BC=0.5.根据规定,地下停
车库破道口上方要张贴限高标志,以便告知驾驶员所驾
车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的
长作为限制的高度。小明和小亮谁说的对?请你判断并计算出正确的结果。
(sin18°≈0.309,cos18°≈0.951,tan18°≈0.325,结果精确到
0.1
米)
16(2)题图
17(1)题图
17.(本小题满分10分
每小题5分)
(1)如图,直线y
=2x+
3与x轴相交于点A,与y轴相交于点B.
①求A,B两点的坐标;
②过B点作直线BP与x轴的正半轴相交于P,且使OP
=
2OA,求ΔABP的面积.
(2)如图,在△AOB中,OA=OB,∠A=30 ,⊙O经过AB的中点E分别交OA、OB于C、D两点,连接CD.
(1)求证:AB是⊙O的切线.
(2)求证:AB∥CD.
(3)若CD=4,求扇形OCED的面积.
18.(本题满分8分)
17(2)题图
初中生对待学习的态度一直是教育工作者关注的问题之一.为此菏泽市教育局对我市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了__________名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
(第18题图)
19.(本题满分10分)我市为绿化城区,计划购买甲、乙两种树苗共计500棵,甲种树苗每棵50元,乙种树苗每棵80元,调查统计得:甲、乙两种树苗的成活率分别为90%、95%.
(1)如果购买两种树苗共用28000元,那么甲、乙两种树苗各买了多少棵?
(2)市绿化部门研究决定,购买树苗的钱数不得超过34000元,应如何选购树苗?
(3)要使这批树苗的成活率不低于92%,且使购买树苗的费用最低,应如何选购树苗?最低费用是多少?
20.(10分)
如图(1),矩形ABCD的一边BC在直角坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(m,0),其中m>0。
(1)求点E、F的坐标(用含m的式子表示);
(2)连接OA,若△OAF是等腰三角形,求m的值;
(3)如图(2),设抛物线y=a(x-m-6)2+h经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值。
第20题图
初三数学试题参考答案
第Ⅰ卷(选择题,共24分)
一、选择题:本大题共8个小题,每小题涂对得3分,满分24分.
题号
1
2
3
4
5
6
7
8
答案
D
D
B
D
C
B
D
D
第Ⅱ卷(非选择题,共76分)
填空题:本大题共6个小题,每小题3分,满分18分.
9.
9.1217X1010
10.
(2,0)
11.
12.
1:3
13.
14.①③⑤
三、解答题:
15(1)
(2)2=2x-1-3
2x=6
x=3
经检验,x=3是原分式方程的解.
16.(1)①证明:∵∠ABC=90°,D为AB延长线上一点,
∴∠ABE=∠CBD=90°,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS);
②解:∵AB=CB,∠ABC=90°,
∴∠CAB=45°,
∵∠CAE=30°,
∴∠BAE=∠CAB﹣∠CAE=45°﹣30°=15°,
∵△ABE≌△CBD,
∴∠BCD=∠BAE=15°,
∴∠BDC=90°﹣∠BCD=90°﹣15°=75°;
(2)解:∵AB⊥BD,
∴∠ABD=90°,
∴BD=AB tan∠BAD=10×tan18°=3.2(m),
∴CD=BD﹣BC=3.2﹣0.5=2.7(m),
∵∠BAD+∠BDA=∠DCE+∠BDA=90°,
∴∠DCE=18°,
∴CE=CD sin∠BDE=2.7×sin18°=2.7×0.95≈2.6(m),
即该地下停车库限高
CE
的长约为
2.6m.
17.解:(1)①∵y=2x+3,
∴当y=0时,x=-;当x=0时,y=3,
∴A(-,0)
B(0,3);
②∵OP=2OA=3,
∴AP=AO+OP=+3=
∴S△ABP=×AP×OB=××3=.
∴S△ABP=。
(2)证明:(1)证明:连接
4分
(2)证明:在
8分
(3)解:,,
12分
18.解:(1)50÷25%=200;(2分)
(2)200-120-50=30(人).画图如下.
(5分)
(3)C所占圆心角度数=360°×(1-25%-60%)=54°.(8分)
(4)80000×(25%+60%)=68000,
∴估计该市初中生中大约有68000名学生学习态度达标.(10分)
19.
设购买甲种树苗x棵,则购买乙种树苗为(500-x)棵,由题意得
50x+80(500-x)=28000.
解得x=400.
所以500-x=100.
答:购买甲种树苗400棵,购买乙种树苗100棵.
4分
(2)由题意得:
解得,(注意
答:购买甲种树苗不少于200棵,其余购买乙种树苗.
8分
(注意:得到购买乙种树苗不多于300棵,其余购买甲种树苗……也对)
(3)由题意得
设购买两种树苗的费用之和为y,
则
在此函数中,y随x的增大而减小,
所以当时,取得最小值,其最小值为
答:购买甲种树苗300棵,购买乙种树苗200棵,即可满足这批树苗的成活率不低于92%,又使购买树苗的费用最低,其最低费用为31000元.
12分
20.解:(1)∵四边形ABCD是矩形,
∴AD=BC=10,AB=CD=8,∠D=∠DCB=∠ABC=90°
由折叠对称性:AF=AD=10,FE=DE
在Rt△ABF中,BF=
∴FC=4
设FE=DE=x,
在Rt△ECF中,42+(8-x)2=x2,
解得x=5,CE=8-x=3
∵B(m,0),
∴E(m+10,3),F(m+6,0)。
(2)分三种情形讨论:
若AO=AF,
∵AB⊥OF,
∴OB=BF=6,
∴m=6
若FO=FA,则m+6=10,解得m=4
若OA=OF,在Rt△AOB中,
∴,解得m=
综上所述:m=6或4或。
(3)由(1)知A(m,8),E(m+10,3),
由题意得
解得
∴M(m+6,-1)
设抛物线的对称轴交AD于G
∴G(m+6,8),
∴AG=6,GM=9
∵∠OAB+∠BAM=90°,∠BAM+∠MAG=90°,
∴∠OAB=∠MAG
又∵∠ABO=∠MGA=90°,
∴△AOB∽△AMG
∴
即
∴m=12。
A
B
D
E
C
F
A
B
C
D
10题图
A
E
B
O
C
D
同课章节目录
