探索勾股定理

课件15张PPT。探索勾股定理郑州市第六十八中学：马胜涛常见数字的平方1211441691962252895766251、首先请你先将课文通读一遍，然后回答下面几个问题
①本节课主要研究的是什么问题？
②这个问题最后形成了什么结论？请详细
进行文字叙述
③这个结论的名称叫做什么？
④这个结论只在什么图形中才存在呢？
所有的这种图形都一定存在这种结论么？预习提纲①对于问题1，请你分别作出如下三个直角三角形，他们的两条直角边分别是 3cm,4cm； 6cm,8cm；5cm,12cm； 然后回答课本问题2、精读课文P2做一做
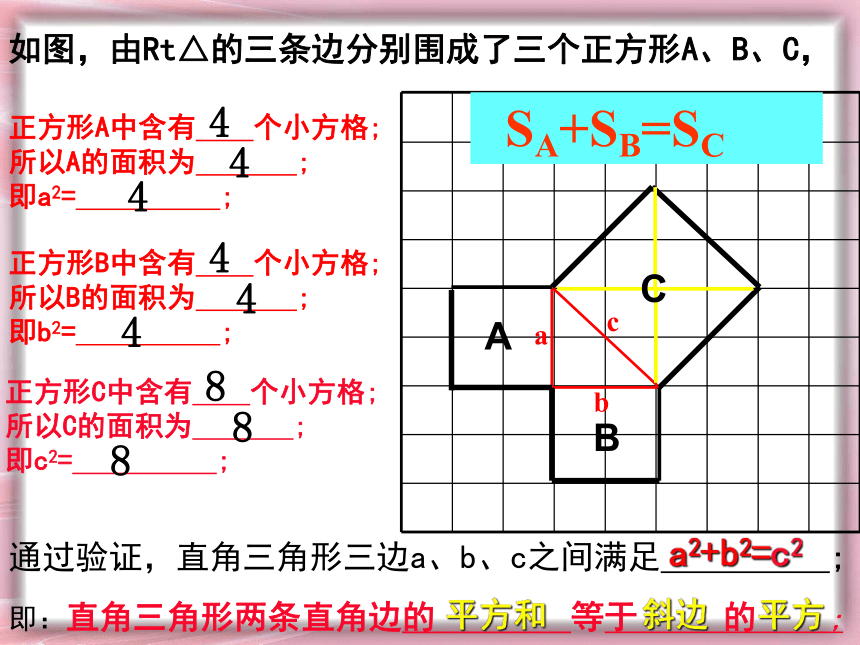
跟随提纲结合课本完成下面题目②对于问题2，你发现图1-2和图1-3中的直角三角形三边的平方与正方形面积之间的关系了么？你能利用正方形A、B、C面积的大小关系，来验证问题2么？ abc正方形A中含有 个小方格;
所以A的面积为 ;
即a2= ; ABC正方形B中含有 个小方格;
所以B的面积为 ;
即b2= ; 正方形C中含有 个小方格;
所以C的面积为 ;
即c2= ; 444444888如图，由Rt△的三条边分别围成了三个正方形A、B、C，通过验证，直角三角形三边a、b、c之间满足 ;
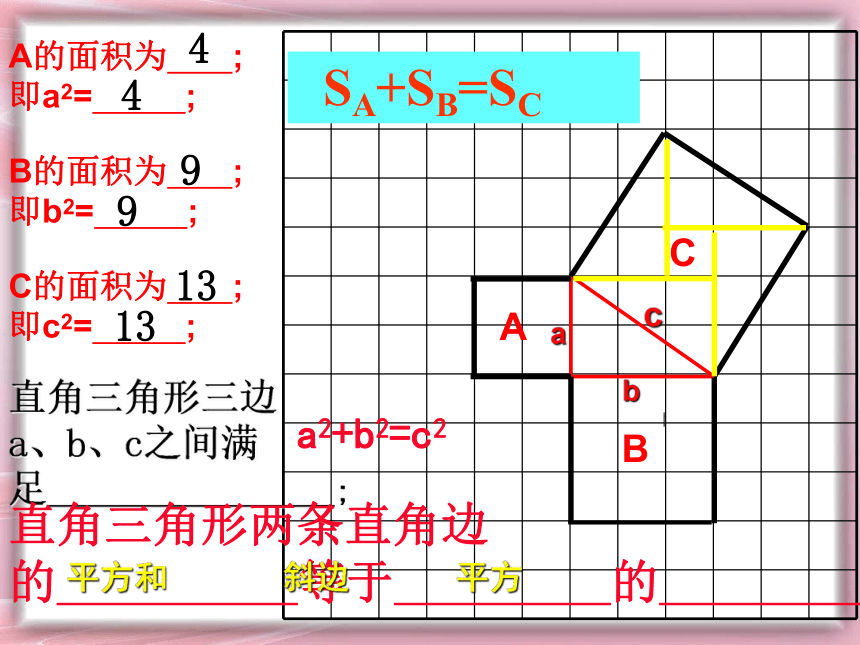
即：直角三角形两条直角边的 等于 的 ; a2+b2=c2 SA+SB=SCabcA的面积为 ;
即a2= ; B的面积为 ;
即b2= ; C的面积为 ;
即c2= ; 直角三角形三边
a、b、c之间满足 ;a2+b2=c2直角三角形两条直角边
的 等于 的 ;44991313 SA+SB=SCAC3、请再次逐字逐句读P4勾股定理内容，仔细阅读几遍后再思考以下问题，切忌：要仔细考虑，确信无误后方可作答
①勾股定理适用于所有的三角形么？
②△ABC三边分别为a,b,c，则一定有a2+b2=c2吗？
③直角三角形中,如果a=3,b=4,那么一定有c=5吗？
④在Rt△ABC中,较短的两边为a,b,较长边为c，则一定有a2+b2=c2吗？
定义:在直角三角形中，两条直角边的平方和，等于斜边的平方.勾股定理我国古代把直角三角形中较短的直角边称为勾 ，较长的直角边称为股 ，斜边称为弦；因此，我们称上面有关直角三角形三边之间关系的结论为勾股定理，也叫毕达格拉斯定理abca2+b2=c2预习检测1、如图，在Rt △ACB中，∠C=90。①若a=3，b=4, 则c =______.
②若a=5，c=13, 则b =_____.
③若a=6，b=8, 则c =______.
④若b=12，c=15, 则a =_____.5121092、下图三角形均为Rt△，求图中字母所代表的边长或正方形的面积1446259 cm210121、一根旗杆在离地面9米处断裂，旗杆顶部落在离旗杆底部12米处，旗杆折断之前有多高？-------勾股定理的应用延伸拓展，格式仿写解：由勾股定理得92+122=225∴旗杆高度=9+15=24 m=1522、求斜边长为17cm，一直角边长15cm的直角三角形的面积.-------勾股定理的应用解：设另一条直角边长为x cm由勾股定理得:延伸拓展，格式仿写x2=172-152∴S△= ×8×15=60 cm22、如图，在四边形ABCD中，∠A=90。,∠CBD=90。 AD=4，AB=3，BC=12, 求正方形DCEF的面积解：在Rt △BAD中BD2=42+32
BD2=25
BD=5在Rt △DBC中DC2=52+122
DC2=169
DC=13∴S正DCEF = 13×13=169 cm2延伸拓展，格式仿写-------勾股定理的应用3、如图，求等腰△ABC的面积5cm5cm6cm解：作CD⊥AB，D则AD=BD=3cm在Rt△ADC中CD2=52 - 32
CD2=16
CD = 4 cm∴S△ABC= ×6×4=12 cm2延伸拓展，格式仿写-------勾股定理的应用课堂小结1、本节课你都学到了哪些知识？2、勾股定理是用来做什么的？3、勾股定理的使用条件？4、用勾股定理解题时格式有怎样的要求？