5.2 万有引力定律的应用 课件 (1)

课件69张PPT。第2节 万有引力定律的应用
第3节 人类对太空的不懈追求1.了解卫星的发射、运行等情况.
2.知道三个宇宙速度的含义,会计算第一宇宙速度.
3.了解海王星的发现过程,掌握研究天体(或卫星)运动的基本方法，并能用万有引力定律解决相关问题.
4.了解人类探索太空的历史、现状及其未来发展的方向. 重点：1.用万有引力定律解决天体运动的基本方法.
2.了解三个宇宙速度的含义.
难点：1.天体(或卫星)的运行规律.
2.理解和区分宇宙速度、发射速度和运行速度.一、人造卫星上天与宇宙速度
1.人造地球卫星的发射原理
(1)牛顿设想：
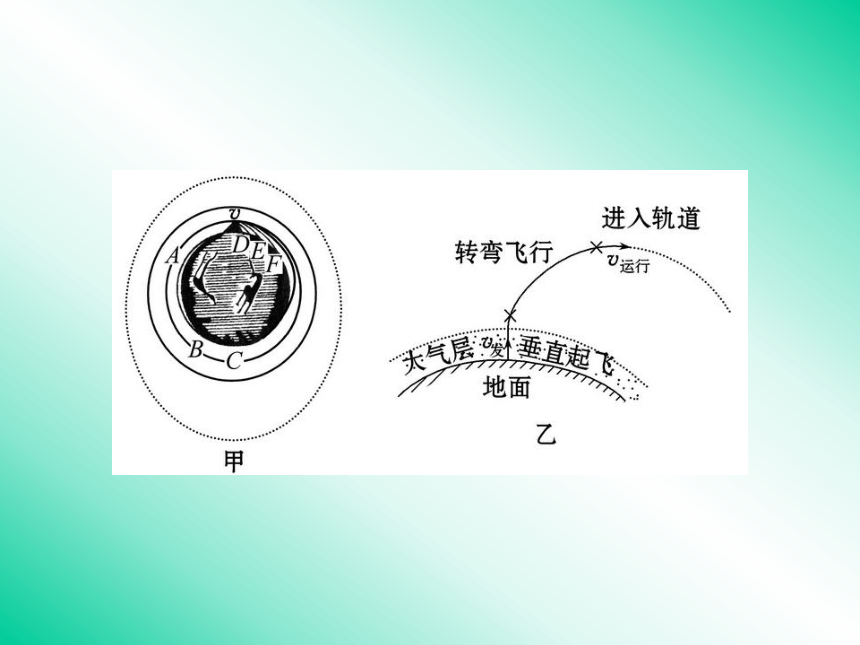
如图甲所示,当物体被抛出的速度_______时,它将围绕地球旋转
而不再落回地面,成为一颗人造地球卫星.足够大(2)发射过程简介：
如图乙所示,发射人造地球卫星的火箭一般为_____.使卫星进入
地球轨道后的大致过程也为三个阶段.
2.动力学特点
一般情况下可认为人造卫星绕地球做_________运动，其向心力
由地球对它的_________提供.三级匀速圆周万有引力3.卫星环绕地球运动的规律
4.宇宙速度
(1)第一宇宙速度：v1=____ km/s，又称_____速度，是人造卫
星在地面附近绕地球做匀速圆周运动的速度.7.9环绕(2)第二宇宙速度：v2=11.2 km/s，又称_____速度，是人造卫
星脱离_____引力所需的速度.
(3)第三宇宙速度：v3=16.7 km/s，又称_____速度，是人造卫
星脱离_____引力所需的速度.脱离地球逃逸太阳【想一想】能否有发射轨道高度不同但具有相同周期的地球卫星？
提示：不能.根据万有引力提供地球卫星做匀速圆周运动的向心力 所以当卫星轨道高度不同时，其周期一定不同，故不能发射在不同轨道高度但具有相同周期的地球卫星.二、人类对太空的探索
1.发现未知天体
在观测天王星时，发现其实际轨道与由_____________计算的轨
道不吻合，由此预测存在另一行星，这就是后来发现的_____星.万有引力定律海王2.人类对太空的不懈追求
(1)古希腊人的探索与文艺复兴时期的学说：地球地球太阳太阳匀速圆周第谷(2)牛顿的大综合：
牛顿在前人的基础上，逐步建立了_____________，将地面上的
力学与天上的力学统一起来，是物理学的第一次大综合，形成
了以_____________为基础的力学体系.
(3)对太空的探索成果：
1957年10月，_______成功发射了第一颗人造地球卫星；
1969年7月，美国“阿波罗”11号登上_____；
2003年10月，_____________发射升空，圆了中国人的飞天梦想.
2012年6月，我国_____________飞船首次完成与“天宫”一号
的手控交会对接任务. 万有引力定律牛顿三大定律前苏联月球“神舟”五号“神舟”九号【想一想】如图所示是航天员翟
志刚走出“神舟七号”飞船进行
舱外活动的精彩瞬间,试问翟志
刚还受重力作用吗?是什么力推
动他随飞船前进的?
提示：翟志刚还受重力作用,且万有引力等于重力.他随飞船前进是惯性表现,没有推动力.　　　　　对卫星的几个速度的理解
【探究导引】如图所示是发射卫星升空的过程和飞船进入轨道后对舱内航天员活动的记录.观察图片,思考以下问题：
(1)发射近地卫星和发射同步卫星,发射的速度一样大吗?
(2)卫星的发射速度与卫星的运行速度是一回事吗?
(3)飞船运行的半径越大时，它运行的速度越大吗?【要点整合】
1.人造卫星的发射速度与运行速度
(1)发射速度:是指在地面上发射卫星时卫星离开发射装置时的初速度,并且卫星一旦离开发射装置后就再无能量补充,依靠自身的惯性在地球引力作用下绕地球运动.显然要发射一颗人造地球卫星,发射的最小速度就是近地卫星做圆周运动的环绕速度,人造卫星的轨道半径越大,火箭要克服地球对它的引力做功越多,发射速度就越大.(2)运行速度:是指卫星进入运行轨道后绕地球做匀速圆周运动
的线速度.由万有引力提供向心力,即
由此可知,卫星的轨道半径越大,其运行速度越小.2.三种宇宙速度
(1)第一宇宙速度(环绕速度)的推导：
方法一：对于近地人造卫星,轨道半径近似等于地球半径R,卫星
在轨道处所受的万有引力近似等于卫星在地面上所受的重力,这
样重力等于向心力,即
把g=9.8 m/s2,R=6 400 km代入,得v≈7.9 km/s.方法二:设地球质量为M,卫星质量为m,卫星绕地球做匀速圆周运
动的半径为r,线速度为v,根据万有引力提供向心力
得 卫星贴近地面运动的半径r ≈R(R为地球半径).取
R=6.4×106 m,M=5.98×1024 kg,则
=7.9 km/s.可见，
7.9 km/s的速度是人造地球卫星在地面附近绕地球做匀速圆周
运动具有的最大运行速度，我们称为第一宇宙速度，也是人造
地球卫星的最小发射速度.当11.2 km/s>v>7.9 km/s时，卫星绕
地球旋转，其轨道是椭圆，地球位于椭圆的一个焦点上.(2)第二宇宙速度(脱离速度):v=11.2 km/s是使人造卫星挣脱地球引力束缚,成为绕太阳运行的人造行星或飞到其他行星上去的最小发射速度.当16.7 km/s>v>11.2 km/s时,卫星脱离地球束缚,成为太阳系的一颗“小行星”，且太阳位于椭圆的一个焦点上.
(3)第三宇宙速度(逃逸速度):v=16.7 km/s是使人造卫星挣脱太阳引力的束缚,飞到太阳系以外的宇宙空间去的最小发射速度.当v≥16.7 km/s时,卫星脱离太阳的引力束缚,跑到太阳系以外的宇宙空间中去.【特别提醒】(1)三种宇宙速度均指在地球上的发射速度.
(2)第一宇宙速度是卫星环绕地球做匀速圆周运动的最大速度,也是卫星的最小发射速度.
(3)轨道半径越大的卫星,其运行速度越小,但其地面发射速度越大.【典例1】(2012·武汉高一检测)“嫦娥二号”是我国月球探测第二期工程的先导星.设该卫星绕月球表面做匀速圆周运动,已知地球的质量是月球质量的81倍,地球半径约为月球半径的4倍.地球卫星的第一宇宙速度约为7.9 km/s,则“嫦娥二号”卫星绕月球运行的最大速度约为( )
A.0.4 km/s B.1.8 km/s
C.11 km/s D.36 km/s【思路点拨】解答本题应把握以下三点：
关键点
(1)明确第一宇宙速度的含义：是近地卫星的环绕速度.
(2)将卫星的运动看做匀速圆周运动，万有引力提供向心力.
(3)采用比例法求解.【规范解答】第一宇宙速度指的是近地卫星的环绕速度，对于贴近地
球表面或月球表面运动的人造卫星，其所受的万有引力提供做匀速圆
周运动所需要的向心力，即 所以
所以
由 知,半径越小,运行速度越大,所以绕月球
表面的卫星运行速度最大,故B正确.
答案：B【总结提升】天体第一宇宙速度的计算方法
对于任何天体，计算其环绕速度时，都是根据万有引力提供向
心力的思路，卫星的轨道半径等于天体的半径，由牛顿第二定律列式计算.
(1)如果知道天体的质量和半径，由 可直接列式计算.
(2)如果不知道天体的质量和半径的具体大小，但知道该天体与
地球的质量、半径关系，可分别列出天体与地球环绕速度的表
达式，用比例法进行计算.【变式训练】某人在一星球上以速率v竖直上抛一物体,经时间t物体以速率v落回手中.已知该星球的半径为R,求该星球上的第一宇宙速度.【解析】根据匀变速运动的规律可得,该星球表面的重力加速度
为
该星球的第一宇宙速度,即卫星在其表面附近绕它做匀速圆周运
动的线速度,该星球对卫星的引力(重力)提供卫星做圆周运动的
向心力,则
该星球表面的第一宇宙速度为
答案:【变式备选】若取地球的第一宇宙速度为8 km/s,某行星质量是地球的6倍，半径是地球的1.5倍，此行星的第一宇宙速度约为
( )
A.16 km/s B.32 km/s
C.4 km/s D.2 km/s【解析】选A.第一宇宙速度是近地卫星的环绕速度，对于近地
卫星，其轨道半径近似等于星球半径，所受万有引力提供其做
匀速圆周运动的向心力，根据万有引力定律和牛顿第二定律得
因为行星的质量M′是地球质量M的6倍，半径R′是地球半径R的
1.5倍，故
即v′=2v=2×8 km/s=16 km/s,A正确.　　　　　卫星的运动规律及其应用
【探究导引】
如图所示是记录的太空中形态各异、大小不同、高低不同的卫星及其运行的轨道.思考以下问题：(1)能发射轨道面与北回归线纬线圈共面的人造卫星吗？
(2)能发射周期为80 min的地球卫星吗？
(3)理论上，每个国家发射的地球同步卫星会在轨道上相撞吗？【要点整合】
1.人造地球卫星的轨道
人造卫星的轨道可以是椭圆轨道，也可以是圆轨道.
(1)椭圆轨道：地心位于椭圆的一个焦点上,卫星的运动遵循开普勒定律.
(2)圆轨道：卫星绕地球做匀速圆周运动，卫星所需的向心力由万有引力提供，由于万有引力指向地心，所以卫星的轨道圆心必然是地心，即卫星在以地心为圆心的轨道平面内绕地球做匀速圆周运动.(3)轨道及其特点:
地球卫星的轨道平面可以与赤道平面成任意角度，但轨道平面一定过地心.当轨道平面与赤道平面重合时，称为赤道轨道；当轨道平面与赤道平面垂直时，即通过极点，称为极地轨道，如图所示.2.卫星的运行特点
(1)由于万有引力提供卫星绕地球运动的向心力,所以有应
用(2)由于卫星轨道的最小半径为r=R(R为地球半径),此时加速度最大,a=g，线速度最大,为第一宇宙速度7.9 km/s,其角速度最大,周期最小,约为85 min.即所有卫星的a、v、ω、T只与轨道半径r有关,而与其他因素无关.3.卫星的“超重”与“失重”
(1)卫星在进入轨道前的加速过程及返回时的减速阶段,由于具有向上的加速度,所以卫星均处于超重状态.
(2)卫星在进入轨道后的正常运转过程中,由于万有引力完全充当向心力,产生指向地心的向心加速度,卫星上的物体对支持面和悬绳无弹力作用,卫星处于完全失重状态.此状态下,在卫星上的仪器,凡制造原理与重力有关的均不能使用.4.地球同步卫星及特点
(1)概念：
地球同步卫星是指在赤道平面内,以和地球自转角速度相同的角速度绕地球运动的卫星,同步卫星又叫通讯卫星.(2)特点：相对地球静止,与地球自转的周期相等,即T=24 h与地球自转的角速度相同与地球自转方向一致与赤道平面共面,即所有的同步卫星都在赤道正
上方 地球对卫星的万有引力提供向心力 离地面高度固定不变,速率一定,向心加速度大小一定,【特别提醒】(1)一般情况下可认为卫星的运动轨迹是圆形.当卫星的运行轨迹为椭圆时,其运动遵循开普勒三定律.
(2)所有卫星在空中运动的v、ω、T、a都是由r决定.r是自变量,前四个量为因变量，与卫星的质量m无关.【典例2】(2012·安徽高考)我国发射的“天宫”一号和“神舟”八号在对接前，“天宫”一号的运行轨道高度为350 km,
“神舟”八号的运行轨道高度为343 km.它们的运行轨道均视为圆周，则( )
A.“天宫”一号比“神舟”八号速度大
B.“天宫”一号比“神舟”八号周期长
C.“天宫”一号比“神舟”八号角速度大
D.“天宫”一号比“神舟”八号加速度大【思路点拨】卫星绕地球做匀速圆周运动时，万有引力提供向心力，根据F万=F向，得出卫星的线速度、周期、角速度、向心加速度与轨道半径r的关系，从而得出“天宫”一号和“神舟”八号各物理量的大小关系.【解题流程】卫星绕地球做匀速圆周运动时由
T天>T神，a天答案：B【总结提升】天体运动的解题技巧
(1)建立模型：
不论是自然天体(如地球、月亮等)还是人造天体(如卫星、飞船等)，只要它们是在绕某一中心天体做圆周运动，就可以将其简化为质点的匀速圆周运动模型.
(2)列方程求解：
根据中心天体对环绕天体的万有引力提供向心力，列出合适的向心力表达式进行求解.(3)巧用“黄金代换GM=gR2”：
若不知天体的质量M，但知道其表面的重力加速度g，则可利用物体在天体表面的重力等于万有引力，列出方程
继而GM=gR2，用gR2替代GM，将问题简单化.【变式训练】(2011·天津高考)质量为m的探月航天器在接近月球表面的轨道上飞行，其运动视为匀速圆周运动，已知月球质量为M，月球半径为R，月球表面重力加速度为g，引力常量为G，不考虑月球自转的影响，则航天器的( )
A.线速度
B.角速度
C.运行周期
D.向心加速度【解析】选A、C.月球对探月航天器的万有引力提供探月航天器
在月球附近做匀速圆周运动所需要的向心力，根据牛顿第二定
律列方程得 则探月航天器的线速度为
选项A正确.其加速度 选项D错误.又知，在
月球附近满足 因此探月航天器的角速度
其周期为 选项B错误，而选项C正确.【变式备选】(2011·北京高考)由于通讯和广播等方面的需要，许多国家发射了地球同步轨道卫星，这些卫星的( )
A.质量可以不同
B.轨道半径可以不同
C.轨道平面可以不同
D.速率可以不同【解析】选A.由万有引力提供卫星的向心力
解得周期 环绕速度 可见周期相同的情况
下轨道半径必然相同，B错误；轨道半径相同,环绕速度必然相
同，D错误；同步卫星相对于地面静止在赤道上空，所有的同步
卫星运行轨道都在赤道上空同一个圆轨道上，C错误；同步卫星
的质量可以不同，A正确.【温馨提示】浩瀚的宇宙中,除有地球绕太阳旋转与卫星绕地球旋转这种典型的运动模型外,还有双星互转、三星互转的模型,多星问题是同学们学习的难点,也是近几年高考中时常考查的问题.【典例】(2012·重庆高考)冥王星与其附近的另一星体卡戎可视为双星系统，质量比约为7∶1，同时绕它们连线上某点O做匀速圆周运动.由此可知，冥王星绕O点运动的( )
A.轨道半径约为卡戎的
B.角速度大小约为卡戎的
C.线速度大小约为卡戎的7倍
D.向心力大小约为卡戎的7倍【思路点拨】解答本题需要明确以下两点：
关键点
(1)双星间的万有引力提供它们做圆周运动的向心力.
(2)双星的角速度相等.【规范解答】可通过以下表格对选项逐一分析.√因为双星始终在一条直线上,所以它们的
角速度一定相等×冥王星与卡戎之间的万有引力是双星做匀速圆
周运动的向心力,即m冥ω2r冥=m卡ω2r卡得答案：A×双星间的万有引力提供它们做圆周运动的向心
力,是一对作用力和反作用力,故向心力相等×同步卫星、近地卫星和赤道上随地球自转物体的比较
近地卫星是轨道半径近似等于地球半径的卫星，卫星做匀速圆周运动的向心力由万有引力提供.同步卫星是在赤道平面内，定点在某一特定高度的卫星，其做匀速圆周运动的向心力由万有引力提供.在赤道上随地球自转做匀速圆周运动的物体是地球的一部分，它不是地球的卫星，充当向心力的是物体所受万有引力与重力之差.近地卫星与同步卫星的共同点是卫星做匀速圆周运动的向心力由万有引力提供；同步卫星与赤道上随地球自转的物体的共同点是具有相同的角速度.当比较近地卫星和赤道上物体的运动规律时，往往借助同步卫星这一纽带，这样会使问题迎刃而解.【案例展示】地球同步卫星离地心距离为r,运行速度为v1,加速度为a1;地球赤道上物体随地球自转的向心加速度为a2,第一宇宙速度为v2,地球半径为R,则( )
A. B.
C. D. 【规范解答】设地球的质量为M，同步卫星的质量为m1，地球赤
道上的物体质量为m2，近地卫星的质量为m2′，根据向心加速度
和角速度的关系有
故 可知选项A正确，B错误.
由万有引力定律得
对同步卫星：
对近地卫星：
由以上两式解得 可知选项D正确，C错误.
答案：A、D 【易错分析】对本题易错选项及错误原因具体分析如下：1.(2012·南京高一检测)把人造地球卫星的运动近似看做匀速圆周运动,则离地球越近的卫星( )
A.质量越大 B.万有引力越大
C.周期越大 D.角速度越大【解析】选D.由万有引力提供向心力得F向=F引
可知离地面越近,周期越小,角速度越大,
且运动快慢与质量无关.所以卫星离地球的远近决定运动
的快慢,与质量无关,故A、C错，D正确.由于卫星质量m不
确定,故无法比较万有引力大小,故B错.2.若地球卫星绕地球做匀速圆周运动，其绕行速度( )
A.一定等于7.9 km/s
B.一定小于7.9 km/s
C.一定大于7.9 km/s
D.介于7.9 km/s～11.2 km/s之间【解析】选B.第一宇宙速度(v1=7.9 km/s)是卫星贴近地表的
环绕速度，实际上卫星都是距离地面一定高度的，由
知，卫星越高，其环绕速度越小，即一定小于7.9 km/s，故B
正确.3.在轨道上运行的人造地球卫星,若卫星上的天线突然折断,则天线将( )
A.做自由落体运动
B.做平抛运动
C.和卫星一起绕地球在同一轨道上运行
D.由于惯性沿轨道切线方向做直线运动
【解析】选C.卫星上折断的天线与卫星的线速度大小相同,由于折断的天线距地心的距离也不变化,所以它和卫星一起绕地球在同一轨道上运行,仍然做匀速圆周运动.故C选项正确.4.(2012·临沂高一检测)如图所示
是在同一轨道平面上的三颗不同的
人造地球卫星,关于各物理量的关
系,下列说法正确的是( )
A.根据
B.根据万有引力定律可知FA>FB>FC
C.角速度ωA>ωB>ωC
D.向心加速度aA系为rA可知 所以vA>vB>vC,A选项错;由于三颗卫星的质量关
系不确定,故万有引力大小不确定,B选项错; 所以
ωA>ωB>ωC,故C选项正确; 所以aA>aB>aC,故D选项错.5.地球同步卫星绕地球运动的周期T1=1天，月球绕地球运行的周期T2=27.3天，已知地球半径R=6 400 km，同步卫星的高度h=3.6×104 km,则月球到地心的距离多大？(保留三位有效数字)【解析】设地球质量为M，同步卫星质量为m1，月球的质量
为m2,月球到地心的距离为r，则
①式除以②式得
答案：3.84×105 km