湖南省娄底市冷水江市铎山中学2015-2016学年八年级(上)期末数学模拟试卷(解析版)
文档属性
| 名称 | 湖南省娄底市冷水江市铎山中学2015-2016学年八年级(上)期末数学模拟试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 170.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-09 00:00:00 | ||
图片预览




文档简介
2015-2016学年湖南省娄底市冷水江市铎山中学八年级(上)期末数学模拟试卷
一、选择题(每小题3分,共30分)
1.的平方根是( )
A.
B.2
C.±2
D.
2.如果分式有意义,则x的取值范围是( )
A.全体实数
B.x=1
C.x≠1
D.x=0
3.不等式8﹣2x>0的解集在数轴上表示正确的是( )
A.
B.
C.
D.
4.等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为( )
A.12
B.15
C.12或15
D.18
5.计算+的结果为( )
A.﹣1
B.1
C.4﹣3
D.7
6.不等式组的整数解有( )
A.1个
B.2个
C.3个
D.4个
7.化简÷(1+)的结果是( )
A.
B.
C.
D.
8.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE
B.AD=AE
C.DA=DE
D.BE=CD
9.如图,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是( )
A.4cm
B.6cm
C.8cm
D.9cm
10.张老师和李老师住在同一个小区,离学校3000米,某天早晨,张老师和李老师分别于7点10分、7点15分离家骑自行车上班,刚好在校门口遇上,已知李老师骑车的速度是张老师的1.2倍,为了求他们各自骑自行车的速度,设张老师骑自行车的速度是x米/分,则可列得方程为( )
A.
B.
C.
D.
二、填空题(每小题3分,共30分)
11.的立方根是 .
12.不等式2x﹣1>3的解集是 .
13.命题“对顶角相等”的逆命题是 .
14.计算的值是 .
15.比较大小: .
16.如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 (添加一个条件即可).
17.如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=125°,则∠ABC= .
18.在等腰三角形中,马彪同学做了如下研究:已知一个角是60°,则另两个角是唯一确定的(60°,60°),已知一个角是90°,则另两个角也是唯一确定的(45°,45°),已知一个角是120°,则另两个角也是唯一确定的(30°,30°).由此马彪同学得出结论:在等腰三角形中,已知一个角的度数,则另两个角的度数也是唯一确定的.马彪同学的结论是 的.(填“正确”或“错误”)
19.化简:
= .
20.已知关于x的方程的解是负数,则n的取值范围为 .
三、计算与解答(共26分)
21.计算:(﹣3)﹣2+|﹣3|﹣+(π﹣3)0.
22.计算:﹣3﹣|﹣4|+.
23.先化简,再求值:,其中a=2,b=.
24.解方程:.
25.解不等式组:并写出它的所有的整数解.
四、操作与证明(共18分)
26.如图所示,点C、D是∠AOB内部的两点.
(1)作∠AOB的平分线OE;
(2)在射线OE上,求作一点P,使PC=PD.(要求用尺规作图,保留作图痕迹)
27.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
28.如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)当∠AEB=50°,求∠EBC的度数.
五、生活与应用(每小题8分,共16分)
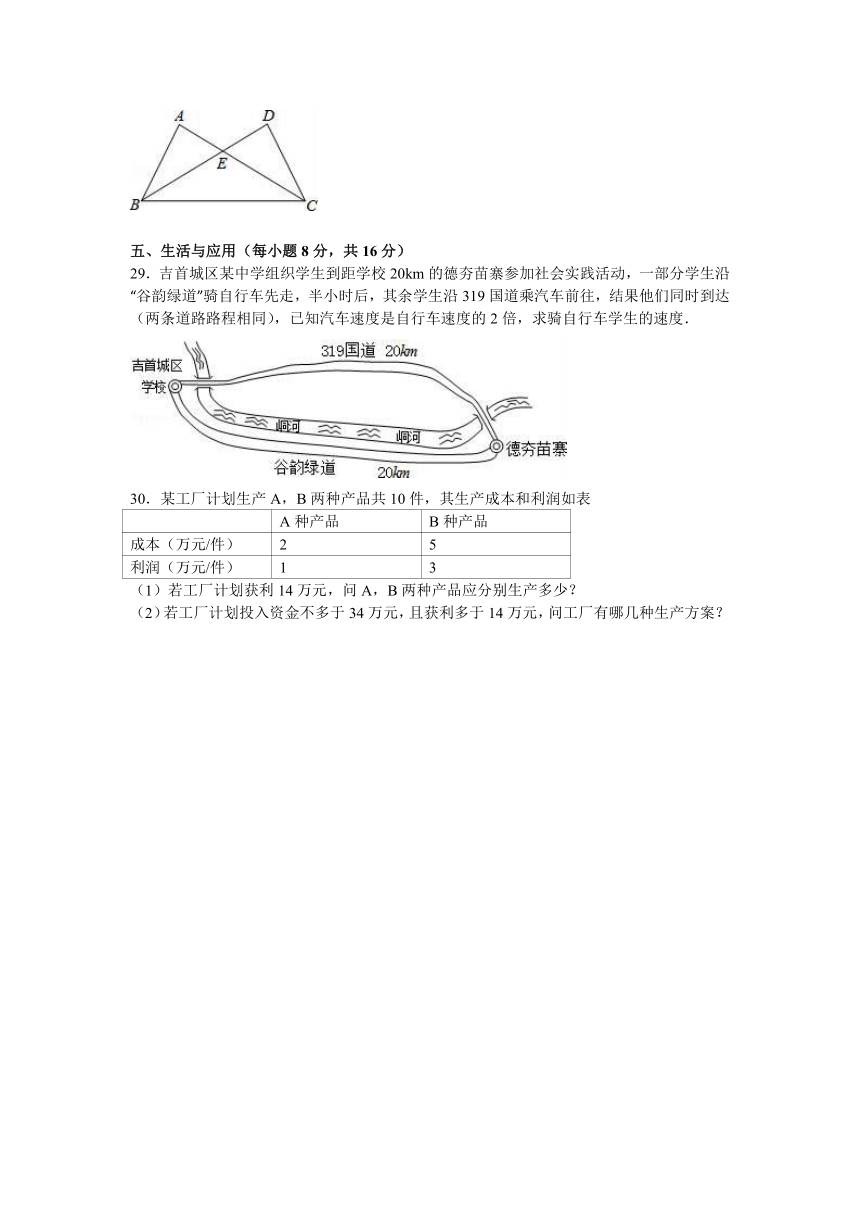
29.吉首城区某中学组织学生到距学校20km的德夯苗寨参加社会实践活动,一部分学生沿“谷韵绿道”骑自行车先走,半小时后,其余学生沿319国道乘汽车前往,结果他们同时到达(两条道路路程相同),已知汽车速度是自行车速度的2倍,求骑自行车学生的速度.
30.某工厂计划生产A,B两种产品共10件,其生产成本和利润如表
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少?
(2)若工厂计划投入资金不多于34万元,且获利多于14万元,问工厂有哪几种生产方案?
2015-2016学年湖南省娄底市冷水江市铎山中学八年级(上)期末数学模拟试卷
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.的平方根是( )
A.
B.2
C.±2
D.
【考点】算术平方根;平方根.
【分析】首先根据算术平方根的定义化简,然后根据平方根的定义即可得出结果.
【解答】解:∵=4,
又∵22=4,(﹣2)2=4,
∴的平方根为±2;
故选C.
2.如果分式有意义,则x的取值范围是( )
A.全体实数
B.x=1
C.x≠1
D.x=0
【考点】分式有意义的条件.
【分析】分式有意义,分母x﹣1≠0,据此可以求得x的取值范围.
【解答】解:当分母x﹣1≠0,即x≠1时,分式有意义.
故选C.
3.不等式8﹣2x>0的解集在数轴上表示正确的是( )
A.
B.
C.
D.
【考点】在数轴上表示不等式的解集;解一元一次不等式.
【分析】先根据不等式的基本性质求出此不等式的解集,在数轴上表示出来,再找出符合条件的选项即可.
【解答】解:移项得,﹣2x>﹣8,
系数化为1得,x<4.
在数轴上表示为:
故选C.
4.等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为( )
A.12
B.15
C.12或15
D.18
【考点】等腰三角形的性质;三角形三边关系.
【分析】因为已知长度为3和6两边,没有明确是底边还是腰,所以有两种情况,需要分类讨论.
【解答】解:①当3为底时,其它两边都为6,
3、6、6可以构成三角形,
周长为15;
②当3为腰时,
其它两边为3和6,
∵3+3=6=6,
∴不能构成三角形,故舍去,
∴答案只有15.
故选B.
5.计算+的结果为( )
A.﹣1
B.1
C.4﹣3
D.7
【考点】实数的运算.
【分析】先算乘法,再算加法即可.
【解答】解:原式=+
=4﹣3
=1.
故选B.
6.不等式组的整数解有( )
A.1个
B.2个
C.3个
D.4个
【考点】一元一次不等式组的整数解.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,从而得知.
【解答】解:解不等式2x﹣1<3,得:x<2,
解不等式﹣0.5x≤1,得:x≥﹣2,
所以不等式组的解集为:﹣2≤x<2,
则其整数解有:﹣2、﹣1、0、1这4个,
故选:D.
7.化简÷(1+)的结果是( )
A.
B.
C.
D.
【考点】分式的混合运算.
【分析】首先对括号内的式子通分相加,然后把除法转化成乘法,进行约分即可.
【解答】解:原式=÷
=
=.
故选A.
8.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE
B.AD=AE
C.DA=DE
D.BE=CD
【考点】等腰三角形的性质.
【分析】根据全等三角形的判定与性质,等边对等角的性质对各选项分析判断后利用排除法求解.
【解答】解:A、添加BD=CE,可以利用“边角边”证明△ABD和△ACE全等,再根据全等三角形对应角相等得到∠DAB=∠EAC,故本选项错误;
B、添加AD=AE,根据等边对等角可得∠ADE=∠AED,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠DAB=∠EAC,故本选项错误;
C、添加DA=DE无法求出∠DAB=∠EAC,故本选项正确;
D、添加BE=CD可以利用“边角边”证明△ABE和△ACD全等,再根据全等三角形对应角相等得到∠DAB=∠EAC,故本选项错误.
故选C.
9.如图,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是( )
A.4cm
B.6cm
C.8cm
D.9cm
【考点】全等三角形的判定与性质.
【分析】求出∠FBD=∠CAD,AD=BD,证△DBF≌△DAC,推出BF=AC,代入求出即可.
【解答】解:∵F是高AD和BE的交点,
∴∠ADC=∠ADB=∠AEF=90°,
∴∠CAD+∠AFE=90°,∠DBF+∠BFD=90°,
∵∠AFE=∠BFD,
∴∠CAD=∠FBD,
∵∠ADB=90°,∠ABC=45°,
∴∠BAD=45°=∠ABD,
∴AD=BD,
在△DBF和△DAC中
∴△DBF≌△DAC(ASA),
∴BF=AC=8cm,
故选C.
10.张老师和李老师住在同一个小区,离学校3000米,某天早晨,张老师和李老师分别于7点10分、7点15分离家骑自行车上班,刚好在校门口遇上,已知李老师骑车的速度是张老师的1.2倍,为了求他们各自骑自行车的速度,设张老师骑自行车的速度是x米/分,则可列得方程为( )
A.
B.
C.
D.
【考点】由实际问题抽象出分式方程.
【分析】设张老师骑自行车的速度是x米/分,则李老师骑自行车的速度是1.2x米/分,根据题意可得等量关系:张老师行驶的路程3000÷他的速度﹣李老师行驶的路程3000÷他的速度=5分钟,根据等量关系列出方程即可.
【解答】解:设张老师骑自行车的速度是x米/分,由题意得:
﹣=5,
故选:A.
二、填空题(每小题3分,共30分)
11.的立方根是 ﹣ .
【考点】立方根.
【分析】如果一个数x的立方等于a,那么x是a的立方根,根据此定义求解即可.
【解答】解:∵(﹣)3=﹣,
∴﹣的立方根根是:﹣.
故答案是:﹣.
12.不等式2x﹣1>3的解集是 x>2 .
【考点】解一元一次不等式;不等式的性质.
【分析】移项后合并同类项得出2x>4,不等式的两边都除以2即可求出答案.
【解答】解:2x﹣1>3,
移项得:2x>3+1,
合并同类项得:2x>4,
不等式的两边都除以2得:x>2,
故答案为:x>2.
13.命题“对顶角相等”的逆命题是 相等的角为对顶角 .
【考点】命题与定理.
【分析】交换原命题的题设与结论即可得到其逆命题.
【解答】解:命题“对顶角相等”的逆命题是“相等的角为对顶角”.
故答案为相等的角为对顶角.
14.计算的值是 2 .
【考点】二次根式的混合运算.
【分析】根据二次根式运算顺序直接运算得出即可.
【解答】解:
=2﹣+
=2.
故答案为:2.
15.比较大小: > .
【考点】实数大小比较.
【分析】利用作差法比较两个数的大小.
【解答】解:∵1<3<4,
∴1<<2,
∴﹣1>0,
∴﹣=>0,
∴>.
故答案是:>.
16.如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 ∠B=∠C或AE=AD (添加一个条件即可).
【考点】全等三角形的判定.
【分析】要使△ABE≌△ACD,已知AB=AC,∠A=∠A,则可以添加一个边从而利用SAS来判定其全等,或添加一个角从而利用AAS来判定其全等.
【解答】解:添加∠B=∠C或AE=AD后可分别根据ASA、SAS判定△ABE≌△ACD.
故答案为:∠B=∠C或AE=AD.
17.如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=125°,则∠ABC= 70° .
【考点】线段垂直平分线的性质;角平分线的性质;等腰三角形的性质.
【分析】先根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠C,再根据线段垂直平分线上的点到线段两端点的距离相等可得OB=OC,根据等边对等角的性质求出∠OBC=∠C,然后根据角平分线的定义解答即可.
【解答】解:∵AD⊥BC,∠AOC=125°,
∴∠C=∠AOC﹣∠ADC=125°﹣90°=35°,
∵D为BC的中点,AD⊥BC,
∴OB=OC,
∴∠OBC=∠C=35°,
∵OB平分∠ABC,
∴∠ABC=2∠OBC=2×35°=70°.
故答案为:70°.
18.在等腰三角形中,马彪同学做了如下研究:已知一个角是60°,则另两个角是唯一确定的(60°,60°),已知一个角是90°,则另两个角也是唯一确定的(45°,45°),已知一个角是120°,则另两个角也是唯一确定的(30°,30°).由此马彪同学得出结论:在等腰三角形中,已知一个角的度数,则另两个角的度数也是唯一确定的.马彪同学的结论是 错误 的.(填“正确”或“错误”)
【考点】等腰三角形的性质.
【分析】分别把已知角看做等腰三角形的顶角和底角,分两种情况考虑,利用三角形内角和是180度计算即可.
【解答】解:如已知一个角=70°.
当70°为顶角时,另外两个角是底角,它们的度数是相等的,为÷2=55°,
当70°为底角时,另外一个底角也是70°,顶角是180°﹣140°=40°.
故答案为:错误.
19.化简:
= .
【考点】分式的加减法.
【分析】先将x2﹣4分解为(x+2)(x﹣2),然后通分,再进行计算.
【解答】解:
===.
20.已知关于x的方程的解是负数,则n的取值范围为 n<2且n≠ .
【考点】分式方程的解.
【分析】求出分式方程的解x=n﹣2,得出n﹣2<0,求出n的范围,根据分式方程得出n﹣2≠﹣,求出n,即可得出答案.
【解答】解:,
解方程得:x=n﹣2,
∵关于x的方程的解是负数,
∴n﹣2<0,
解得:n<2,
又∵原方程有意义的条件为:x≠﹣,
∴n﹣2≠﹣,
即n≠.
故答案为:n<2且n≠.
三、计算与解答(共26分)
21.计算:(﹣3)﹣2+|﹣3|﹣+(π﹣3)0.
【考点】实数的运算;零指数幂;负整数指数幂.
【分析】原式第一项利用负整数指数幂法则计算,第二项利用绝对值的代数意义化简,第三项利用算术平方根定义计算,第四项利用零指数幂法则计算即可得到结果.
【解答】解:原式=+3﹣3+1=.
22.计算:﹣3﹣|﹣4|+.
【考点】二次根式的加减法.
【分析】首先化简二次根式,进而合并求出答案.
【解答】解:原式=3﹣﹣4+3
=2﹣.
23.先化简,再求值:,其中a=2,b=.
【考点】分式的化简求值.
【分析】先把括号内通分,再把除法运算化为乘法运算,然后把a2﹣b2分解因式后约分得到原式=,再把a和b的值代入计算即可.
【解答】解:原式=÷
=
=,
当a=2,b=时,原式==2+.
24.解方程:.
【考点】解分式方程.
【分析】先去分母把分式方程化为整式方程,求出整式方程中x的值,代入公分母进行检验即可.
【解答】解:方程两边同时乘以2(3x﹣1),得4﹣2(3x﹣1)=3,
化简,﹣6x=﹣3,解得x=.
检验:x=时,2(3x﹣1)=2×(3×﹣1)≠0
所以,x=是原方程的解.
25.解不等式组:并写出它的所有的整数解.
【考点】解一元一次不等式组;一元一次不等式组的整数解.
【分析】先求出两个不等式的解集,再求其公共解,然后写出整数解即可.
【解答】解:,
解不等式①得,x≥1,
解不等式②得,x<4,
所以,不等式组的解集是1≤x<4,
所以,不等式组的所有整数解是1、2、3.
四、操作与证明(共18分)
26.如图所示,点C、D是∠AOB内部的两点.
(1)作∠AOB的平分线OE;
(2)在射线OE上,求作一点P,使PC=PD.(要求用尺规作图,保留作图痕迹)
【考点】作图—基本作图.
【分析】(1)根据赔付风险的画法画出图形即可.
(2)画出作线段CD的垂直平分线MN,即可解决问题.
【解答】解:(1)∠AOB的平分想如图所示,
(2)作线段CD的垂直平分线MN与射线OE交于点P.
点P就是所求的点.
27.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
【考点】线段垂直平分线的性质;等腰三角形的性质.
【分析】(1)ED是AC的垂直平分线,可得AE=EC;∠A=∠C;已知∠A=36,即可求得;
(2)△ABC中,AB=AC,∠A=36°,可得∠B=72°又∠BEC=∠A+∠ECA=72°,所以,得BC=EC=5;
【解答】解:(1)∵DE垂直平分AC,
∴CE=AE,∴∠ECD=∠A=36°;
(2)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∴∠BEC=∠A+∠ECD=72°,
∴∠BEC=∠B,
∴BC=EC=5.
答:(1)∠ECD的度数是36°;
(2)BC长是5.
28.如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)当∠AEB=50°,求∠EBC的度数.
【考点】全等三角形的判定与性质.
【分析】(1)根据AAS即可推出△ABE和△DCE全等;
(2)根据三角形全等得出EB=EC,推出∠EBC=∠ECB,根据三角形的外角性质得出∠AEB=2∠EBC,代入求出即可.
【解答】(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS);
(2)解:∵△ABE≌△DCE,
∴BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
五、生活与应用(每小题8分,共16分)
29.吉首城区某中学组织学生到距学校20km的德夯苗寨参加社会实践活动,一部分学生沿“谷韵绿道”骑自行车先走,半小时后,其余学生沿319国道乘汽车前往,结果他们同时到达(两条道路路程相同),已知汽车速度是自行车速度的2倍,求骑自行车学生的速度.
【考点】分式方程的应用.
【分析】首先设骑自行车学生的速度是x千米/时,则汽车速度是2x千米/时,由题意可得等量关系;骑自行车学生行驶20千米所用时间﹣汽车行驶20千米所用时间=,根据等量关系,列出方程即可.
【解答】解:设骑自行车学生的速度是x千米/时,由题意得:
﹣=,
解得:x=20,
经检验:x=20是原分式方程的解,
答:骑自行车学生的速度是20千米/时.
30.某工厂计划生产A,B两种产品共10件,其生产成本和利润如表
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少?
(2)若工厂计划投入资金不多于34万元,且获利多于14万元,问工厂有哪几种生产方案?
【考点】一元一次不等式组的应用;一元一次方程的应用.
【分析】(1)设A种产品应生产x件,则B种产品应生产(10﹣x)件,列出方程即可解决.
(2)设A种产品应生产m件,则B种产品应生产(10﹣m)件,列出不等式组解决问题.
【解答】解:(1)设A种产品应生产x件,则B种产品应生产(10﹣x)件,
由题意,x+3(10﹣x)=14,
解得x=8,
∴10﹣x=2,
∴A种产品应生产8件,B种产品应生产2件.
(2)设A种产品应生产m件,则B种产品应生产(10﹣m)件,
由题意得,
解这个不等式组,得,
∵m为正整数,m可以取6或7;
∴生产方案有两种:
①生产A种产品6件,B种产品4件;
②生产A种产品7件,B种产品3件.
2016年8月9日
一、选择题(每小题3分,共30分)
1.的平方根是( )
A.
B.2
C.±2
D.
2.如果分式有意义,则x的取值范围是( )
A.全体实数
B.x=1
C.x≠1
D.x=0
3.不等式8﹣2x>0的解集在数轴上表示正确的是( )
A.
B.
C.
D.
4.等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为( )
A.12
B.15
C.12或15
D.18
5.计算+的结果为( )
A.﹣1
B.1
C.4﹣3
D.7
6.不等式组的整数解有( )
A.1个
B.2个
C.3个
D.4个
7.化简÷(1+)的结果是( )
A.
B.
C.
D.
8.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE
B.AD=AE
C.DA=DE
D.BE=CD
9.如图,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是( )
A.4cm
B.6cm
C.8cm
D.9cm
10.张老师和李老师住在同一个小区,离学校3000米,某天早晨,张老师和李老师分别于7点10分、7点15分离家骑自行车上班,刚好在校门口遇上,已知李老师骑车的速度是张老师的1.2倍,为了求他们各自骑自行车的速度,设张老师骑自行车的速度是x米/分,则可列得方程为( )
A.
B.
C.
D.
二、填空题(每小题3分,共30分)
11.的立方根是 .
12.不等式2x﹣1>3的解集是 .
13.命题“对顶角相等”的逆命题是 .
14.计算的值是 .
15.比较大小: .
16.如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 (添加一个条件即可).
17.如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=125°,则∠ABC= .
18.在等腰三角形中,马彪同学做了如下研究:已知一个角是60°,则另两个角是唯一确定的(60°,60°),已知一个角是90°,则另两个角也是唯一确定的(45°,45°),已知一个角是120°,则另两个角也是唯一确定的(30°,30°).由此马彪同学得出结论:在等腰三角形中,已知一个角的度数,则另两个角的度数也是唯一确定的.马彪同学的结论是 的.(填“正确”或“错误”)
19.化简:
= .
20.已知关于x的方程的解是负数,则n的取值范围为 .
三、计算与解答(共26分)
21.计算:(﹣3)﹣2+|﹣3|﹣+(π﹣3)0.
22.计算:﹣3﹣|﹣4|+.
23.先化简,再求值:,其中a=2,b=.
24.解方程:.
25.解不等式组:并写出它的所有的整数解.
四、操作与证明(共18分)
26.如图所示,点C、D是∠AOB内部的两点.
(1)作∠AOB的平分线OE;
(2)在射线OE上,求作一点P,使PC=PD.(要求用尺规作图,保留作图痕迹)
27.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
28.如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)当∠AEB=50°,求∠EBC的度数.
五、生活与应用(每小题8分,共16分)
29.吉首城区某中学组织学生到距学校20km的德夯苗寨参加社会实践活动,一部分学生沿“谷韵绿道”骑自行车先走,半小时后,其余学生沿319国道乘汽车前往,结果他们同时到达(两条道路路程相同),已知汽车速度是自行车速度的2倍,求骑自行车学生的速度.
30.某工厂计划生产A,B两种产品共10件,其生产成本和利润如表
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少?
(2)若工厂计划投入资金不多于34万元,且获利多于14万元,问工厂有哪几种生产方案?
2015-2016学年湖南省娄底市冷水江市铎山中学八年级(上)期末数学模拟试卷
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.的平方根是( )
A.
B.2
C.±2
D.
【考点】算术平方根;平方根.
【分析】首先根据算术平方根的定义化简,然后根据平方根的定义即可得出结果.
【解答】解:∵=4,
又∵22=4,(﹣2)2=4,
∴的平方根为±2;
故选C.
2.如果分式有意义,则x的取值范围是( )
A.全体实数
B.x=1
C.x≠1
D.x=0
【考点】分式有意义的条件.
【分析】分式有意义,分母x﹣1≠0,据此可以求得x的取值范围.
【解答】解:当分母x﹣1≠0,即x≠1时,分式有意义.
故选C.
3.不等式8﹣2x>0的解集在数轴上表示正确的是( )
A.
B.
C.
D.
【考点】在数轴上表示不等式的解集;解一元一次不等式.
【分析】先根据不等式的基本性质求出此不等式的解集,在数轴上表示出来,再找出符合条件的选项即可.
【解答】解:移项得,﹣2x>﹣8,
系数化为1得,x<4.
在数轴上表示为:
故选C.
4.等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为( )
A.12
B.15
C.12或15
D.18
【考点】等腰三角形的性质;三角形三边关系.
【分析】因为已知长度为3和6两边,没有明确是底边还是腰,所以有两种情况,需要分类讨论.
【解答】解:①当3为底时,其它两边都为6,
3、6、6可以构成三角形,
周长为15;
②当3为腰时,
其它两边为3和6,
∵3+3=6=6,
∴不能构成三角形,故舍去,
∴答案只有15.
故选B.
5.计算+的结果为( )
A.﹣1
B.1
C.4﹣3
D.7
【考点】实数的运算.
【分析】先算乘法,再算加法即可.
【解答】解:原式=+
=4﹣3
=1.
故选B.
6.不等式组的整数解有( )
A.1个
B.2个
C.3个
D.4个
【考点】一元一次不等式组的整数解.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,从而得知.
【解答】解:解不等式2x﹣1<3,得:x<2,
解不等式﹣0.5x≤1,得:x≥﹣2,
所以不等式组的解集为:﹣2≤x<2,
则其整数解有:﹣2、﹣1、0、1这4个,
故选:D.
7.化简÷(1+)的结果是( )
A.
B.
C.
D.
【考点】分式的混合运算.
【分析】首先对括号内的式子通分相加,然后把除法转化成乘法,进行约分即可.
【解答】解:原式=÷
=
=.
故选A.
8.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE
B.AD=AE
C.DA=DE
D.BE=CD
【考点】等腰三角形的性质.
【分析】根据全等三角形的判定与性质,等边对等角的性质对各选项分析判断后利用排除法求解.
【解答】解:A、添加BD=CE,可以利用“边角边”证明△ABD和△ACE全等,再根据全等三角形对应角相等得到∠DAB=∠EAC,故本选项错误;
B、添加AD=AE,根据等边对等角可得∠ADE=∠AED,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠DAB=∠EAC,故本选项错误;
C、添加DA=DE无法求出∠DAB=∠EAC,故本选项正确;
D、添加BE=CD可以利用“边角边”证明△ABE和△ACD全等,再根据全等三角形对应角相等得到∠DAB=∠EAC,故本选项错误.
故选C.
9.如图,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是( )
A.4cm
B.6cm
C.8cm
D.9cm
【考点】全等三角形的判定与性质.
【分析】求出∠FBD=∠CAD,AD=BD,证△DBF≌△DAC,推出BF=AC,代入求出即可.
【解答】解:∵F是高AD和BE的交点,
∴∠ADC=∠ADB=∠AEF=90°,
∴∠CAD+∠AFE=90°,∠DBF+∠BFD=90°,
∵∠AFE=∠BFD,
∴∠CAD=∠FBD,
∵∠ADB=90°,∠ABC=45°,
∴∠BAD=45°=∠ABD,
∴AD=BD,
在△DBF和△DAC中
∴△DBF≌△DAC(ASA),
∴BF=AC=8cm,
故选C.
10.张老师和李老师住在同一个小区,离学校3000米,某天早晨,张老师和李老师分别于7点10分、7点15分离家骑自行车上班,刚好在校门口遇上,已知李老师骑车的速度是张老师的1.2倍,为了求他们各自骑自行车的速度,设张老师骑自行车的速度是x米/分,则可列得方程为( )
A.
B.
C.
D.
【考点】由实际问题抽象出分式方程.
【分析】设张老师骑自行车的速度是x米/分,则李老师骑自行车的速度是1.2x米/分,根据题意可得等量关系:张老师行驶的路程3000÷他的速度﹣李老师行驶的路程3000÷他的速度=5分钟,根据等量关系列出方程即可.
【解答】解:设张老师骑自行车的速度是x米/分,由题意得:
﹣=5,
故选:A.
二、填空题(每小题3分,共30分)
11.的立方根是 ﹣ .
【考点】立方根.
【分析】如果一个数x的立方等于a,那么x是a的立方根,根据此定义求解即可.
【解答】解:∵(﹣)3=﹣,
∴﹣的立方根根是:﹣.
故答案是:﹣.
12.不等式2x﹣1>3的解集是 x>2 .
【考点】解一元一次不等式;不等式的性质.
【分析】移项后合并同类项得出2x>4,不等式的两边都除以2即可求出答案.
【解答】解:2x﹣1>3,
移项得:2x>3+1,
合并同类项得:2x>4,
不等式的两边都除以2得:x>2,
故答案为:x>2.
13.命题“对顶角相等”的逆命题是 相等的角为对顶角 .
【考点】命题与定理.
【分析】交换原命题的题设与结论即可得到其逆命题.
【解答】解:命题“对顶角相等”的逆命题是“相等的角为对顶角”.
故答案为相等的角为对顶角.
14.计算的值是 2 .
【考点】二次根式的混合运算.
【分析】根据二次根式运算顺序直接运算得出即可.
【解答】解:
=2﹣+
=2.
故答案为:2.
15.比较大小: > .
【考点】实数大小比较.
【分析】利用作差法比较两个数的大小.
【解答】解:∵1<3<4,
∴1<<2,
∴﹣1>0,
∴﹣=>0,
∴>.
故答案是:>.
16.如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 ∠B=∠C或AE=AD (添加一个条件即可).
【考点】全等三角形的判定.
【分析】要使△ABE≌△ACD,已知AB=AC,∠A=∠A,则可以添加一个边从而利用SAS来判定其全等,或添加一个角从而利用AAS来判定其全等.
【解答】解:添加∠B=∠C或AE=AD后可分别根据ASA、SAS判定△ABE≌△ACD.
故答案为:∠B=∠C或AE=AD.
17.如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=125°,则∠ABC= 70° .
【考点】线段垂直平分线的性质;角平分线的性质;等腰三角形的性质.
【分析】先根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠C,再根据线段垂直平分线上的点到线段两端点的距离相等可得OB=OC,根据等边对等角的性质求出∠OBC=∠C,然后根据角平分线的定义解答即可.
【解答】解:∵AD⊥BC,∠AOC=125°,
∴∠C=∠AOC﹣∠ADC=125°﹣90°=35°,
∵D为BC的中点,AD⊥BC,
∴OB=OC,
∴∠OBC=∠C=35°,
∵OB平分∠ABC,
∴∠ABC=2∠OBC=2×35°=70°.
故答案为:70°.
18.在等腰三角形中,马彪同学做了如下研究:已知一个角是60°,则另两个角是唯一确定的(60°,60°),已知一个角是90°,则另两个角也是唯一确定的(45°,45°),已知一个角是120°,则另两个角也是唯一确定的(30°,30°).由此马彪同学得出结论:在等腰三角形中,已知一个角的度数,则另两个角的度数也是唯一确定的.马彪同学的结论是 错误 的.(填“正确”或“错误”)
【考点】等腰三角形的性质.
【分析】分别把已知角看做等腰三角形的顶角和底角,分两种情况考虑,利用三角形内角和是180度计算即可.
【解答】解:如已知一个角=70°.
当70°为顶角时,另外两个角是底角,它们的度数是相等的,为÷2=55°,
当70°为底角时,另外一个底角也是70°,顶角是180°﹣140°=40°.
故答案为:错误.
19.化简:
= .
【考点】分式的加减法.
【分析】先将x2﹣4分解为(x+2)(x﹣2),然后通分,再进行计算.
【解答】解:
===.
20.已知关于x的方程的解是负数,则n的取值范围为 n<2且n≠ .
【考点】分式方程的解.
【分析】求出分式方程的解x=n﹣2,得出n﹣2<0,求出n的范围,根据分式方程得出n﹣2≠﹣,求出n,即可得出答案.
【解答】解:,
解方程得:x=n﹣2,
∵关于x的方程的解是负数,
∴n﹣2<0,
解得:n<2,
又∵原方程有意义的条件为:x≠﹣,
∴n﹣2≠﹣,
即n≠.
故答案为:n<2且n≠.
三、计算与解答(共26分)
21.计算:(﹣3)﹣2+|﹣3|﹣+(π﹣3)0.
【考点】实数的运算;零指数幂;负整数指数幂.
【分析】原式第一项利用负整数指数幂法则计算,第二项利用绝对值的代数意义化简,第三项利用算术平方根定义计算,第四项利用零指数幂法则计算即可得到结果.
【解答】解:原式=+3﹣3+1=.
22.计算:﹣3﹣|﹣4|+.
【考点】二次根式的加减法.
【分析】首先化简二次根式,进而合并求出答案.
【解答】解:原式=3﹣﹣4+3
=2﹣.
23.先化简,再求值:,其中a=2,b=.
【考点】分式的化简求值.
【分析】先把括号内通分,再把除法运算化为乘法运算,然后把a2﹣b2分解因式后约分得到原式=,再把a和b的值代入计算即可.
【解答】解:原式=÷
=
=,
当a=2,b=时,原式==2+.
24.解方程:.
【考点】解分式方程.
【分析】先去分母把分式方程化为整式方程,求出整式方程中x的值,代入公分母进行检验即可.
【解答】解:方程两边同时乘以2(3x﹣1),得4﹣2(3x﹣1)=3,
化简,﹣6x=﹣3,解得x=.
检验:x=时,2(3x﹣1)=2×(3×﹣1)≠0
所以,x=是原方程的解.
25.解不等式组:并写出它的所有的整数解.
【考点】解一元一次不等式组;一元一次不等式组的整数解.
【分析】先求出两个不等式的解集,再求其公共解,然后写出整数解即可.
【解答】解:,
解不等式①得,x≥1,
解不等式②得,x<4,
所以,不等式组的解集是1≤x<4,
所以,不等式组的所有整数解是1、2、3.
四、操作与证明(共18分)
26.如图所示,点C、D是∠AOB内部的两点.
(1)作∠AOB的平分线OE;
(2)在射线OE上,求作一点P,使PC=PD.(要求用尺规作图,保留作图痕迹)
【考点】作图—基本作图.
【分析】(1)根据赔付风险的画法画出图形即可.
(2)画出作线段CD的垂直平分线MN,即可解决问题.
【解答】解:(1)∠AOB的平分想如图所示,
(2)作线段CD的垂直平分线MN与射线OE交于点P.
点P就是所求的点.
27.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
【考点】线段垂直平分线的性质;等腰三角形的性质.
【分析】(1)ED是AC的垂直平分线,可得AE=EC;∠A=∠C;已知∠A=36,即可求得;
(2)△ABC中,AB=AC,∠A=36°,可得∠B=72°又∠BEC=∠A+∠ECA=72°,所以,得BC=EC=5;
【解答】解:(1)∵DE垂直平分AC,
∴CE=AE,∴∠ECD=∠A=36°;
(2)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∴∠BEC=∠A+∠ECD=72°,
∴∠BEC=∠B,
∴BC=EC=5.
答:(1)∠ECD的度数是36°;
(2)BC长是5.
28.如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)当∠AEB=50°,求∠EBC的度数.
【考点】全等三角形的判定与性质.
【分析】(1)根据AAS即可推出△ABE和△DCE全等;
(2)根据三角形全等得出EB=EC,推出∠EBC=∠ECB,根据三角形的外角性质得出∠AEB=2∠EBC,代入求出即可.
【解答】(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS);
(2)解:∵△ABE≌△DCE,
∴BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
五、生活与应用(每小题8分,共16分)
29.吉首城区某中学组织学生到距学校20km的德夯苗寨参加社会实践活动,一部分学生沿“谷韵绿道”骑自行车先走,半小时后,其余学生沿319国道乘汽车前往,结果他们同时到达(两条道路路程相同),已知汽车速度是自行车速度的2倍,求骑自行车学生的速度.
【考点】分式方程的应用.
【分析】首先设骑自行车学生的速度是x千米/时,则汽车速度是2x千米/时,由题意可得等量关系;骑自行车学生行驶20千米所用时间﹣汽车行驶20千米所用时间=,根据等量关系,列出方程即可.
【解答】解:设骑自行车学生的速度是x千米/时,由题意得:
﹣=,
解得:x=20,
经检验:x=20是原分式方程的解,
答:骑自行车学生的速度是20千米/时.
30.某工厂计划生产A,B两种产品共10件,其生产成本和利润如表
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少?
(2)若工厂计划投入资金不多于34万元,且获利多于14万元,问工厂有哪几种生产方案?
【考点】一元一次不等式组的应用;一元一次方程的应用.
【分析】(1)设A种产品应生产x件,则B种产品应生产(10﹣x)件,列出方程即可解决.
(2)设A种产品应生产m件,则B种产品应生产(10﹣m)件,列出不等式组解决问题.
【解答】解:(1)设A种产品应生产x件,则B种产品应生产(10﹣x)件,
由题意,x+3(10﹣x)=14,
解得x=8,
∴10﹣x=2,
∴A种产品应生产8件,B种产品应生产2件.
(2)设A种产品应生产m件,则B种产品应生产(10﹣m)件,
由题意得,
解这个不等式组,得,
∵m为正整数,m可以取6或7;
∴生产方案有两种:
①生产A种产品6件,B种产品4件;
②生产A种产品7件,B种产品3件.
2016年8月9日
同课章节目录
