3.1 匀变速直线运动的规律 学案 (8)
文档属性
| 名称 | 3.1 匀变速直线运动的规律 学案 (8) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-08-13 10:48:14 | ||
图片预览

文档简介
第1节 匀变速直线运动的规律
一、匀变速直线运动的基本规律
1.匀变速直线运动的特点:加速度a恒定且轨迹为直线。
2.匀变速直线运动的基本公式
(1)速度—时间公式:vt=v0+at。
(2)位移—时间公式:s=v0t+at2。
(3)位移—速度—加速度公式2as=v-v。
你知道上述公式是怎样推得的吗?
答案:由a==得vt=v0+at
由s=t=·t得s=v0t+at2
或由v-t图象推导,由图象与横轴所构成面积求得
s梯形=s=v0t+at2
将速度中的t代入位移公式得2as=v-v。
3.匀变速直线运动的图象描述
如图所示甲图中甲、乙的加速度有何关系?丙一直做匀变速运动吗?
答案:甲、乙的加速度相等,因为图象平行,图象的斜率表示加速度,所以甲、乙加速度相同;同理丙一直做匀变速直线运动,t1时刻前a<0,v0>0,做匀减速直线运动,t1时刻后a<0,v<0,做反方向匀加速直线运动。
【例1】如图所示,小球以6
m/s的速度由足够长的斜面中部沿着斜面向上滑。已知小球在斜面上运动的加速度大小为2
m/s2,则小球的速度大小何时达到3
m/s?(小球在光滑斜面上运动时,加速度的大小、方向都不改变)
解析:小球先沿斜面向上做匀减速直线运动,速度由6
m/s逐渐减小到零,然后又反向做匀加速直线运动。取沿斜面向上的方向为正方向,则v0=6
m/s,a=-2
m/s2,小球的速度大小为3
m/s有两种情况:向上滑时v1=3
m/s,向下滑时v2=-3
m/s。由公式v=v0+at得t=,所以t1==
s=1.5
s,t2==
s=4.5
s。
答案:1.5
s或4.5
s
在审题时,应格外关注以下词语:“速度大小达到3
m/s”,说明只确定了大小,没确定方向,方向分两种情况讨论。
1-1某物体做匀变速直线运动,某时刻速度的大小为4
m/s,2
s后速度的大小变为8
m/s,在这2
s内物体的( )
A.加速度方向与初速度方向相同
B.加速度方向与末速度方向相同
C.加速度的大小可能小于2
m/s2
D.加速度的大小可能大于4
m/s2
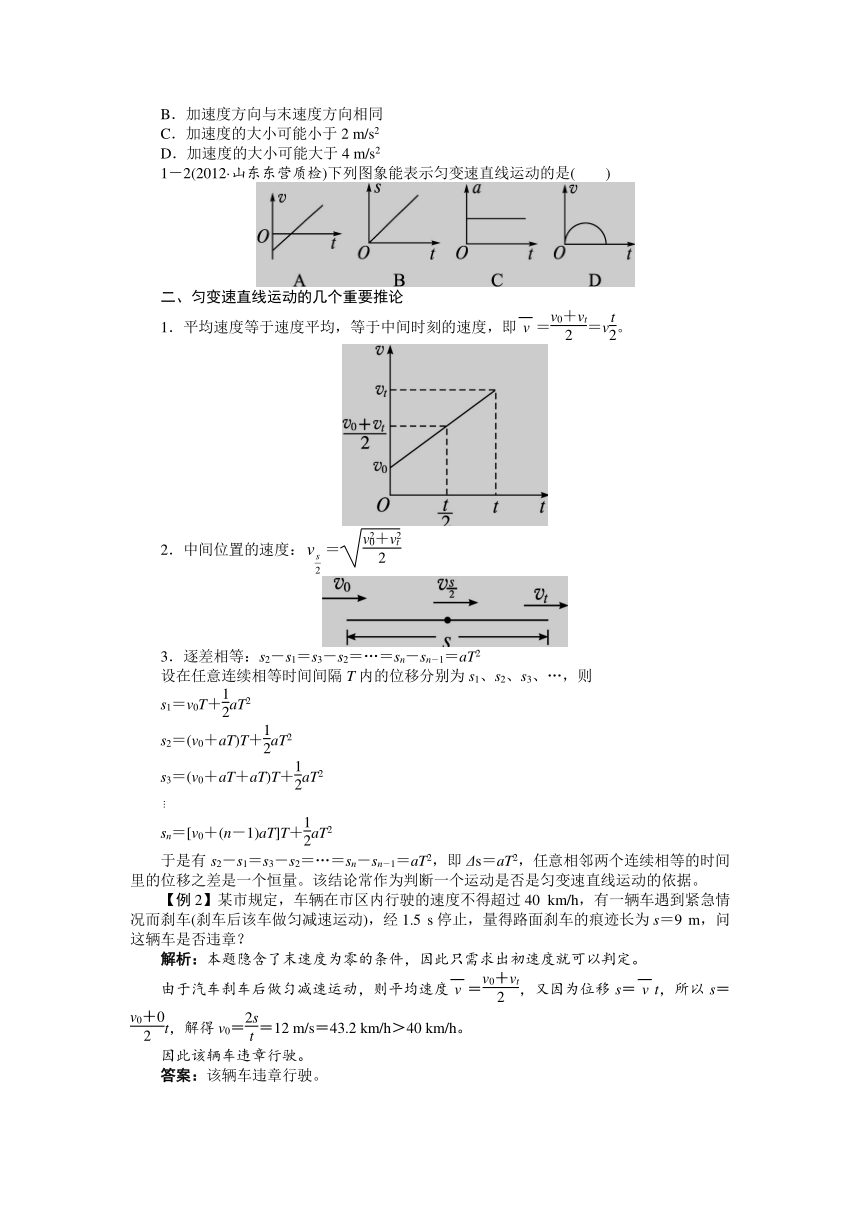
1-2(2012·山东东营质检)下列图象能表示匀变速直线运动的是( )
二、匀变速直线运动的几个重要推论
1.平均速度等于速度平均,等于中间时刻的速度,即==v。
2.中间位置的速度:=
3.逐差相等:s2-s1=s3-s2=…=sn-sn-1=aT2
设在任意连续相等时间间隔T内的位移分别为s1、s2、s3、…,则
s1=v0T+aT2
s2=(v0+aT)T+aT2
s3=(v0+aT+aT)T+aT2
sn=[v0+(n-1)aT]T+aT2
于是有s2-s1=s3-s2=…=sn-sn-1=aT2,即Δs=aT2,任意相邻两个连续相等的时间里的位移之差是一个恒量。该结论常作为判断一个运动是否是匀变速直线运动的依据。
【例2】某市规定,车辆在市区内行驶的速度不得超过40
km/h,有一辆车遇到紧急情况而刹车(刹车后该车做匀减速运动),经1.5
s停止,量得路面刹车的痕迹长为s=9
m,问这辆车是否违章?
解析:本题隐含了末速度为零的条件,因此只需求出初速度就可以判定。
由于汽车刹车后做匀减速运动,则平均速度=,又因为位移s=t,所以s=t,解得v0==12
m/s=43.2
km/h>40
km/h。
因此该辆车违章行驶。
答案:该辆车违章行驶。
2-1某物体做匀变速直线运动,其在第3
s内发生15
m的位移,在第9
s内发生9
m的位移,问其加速度为多大?
2-2做匀变速直线运动的物体先后通过A、B两点,通过A、B点的瞬时速度分别为vA和vB.若物体通过A、B连线中点C的瞬时速度为v1,通过A到B所用时间中间时刻的瞬时速度为v2,关于v1、v2的大小,下列说法正确的是( )
A.若做匀加速直线运动,则v1>v2
B.若做匀减速直线运动,则v1>v2
C.若做匀加速直线运动,则v1<v2
D.若做匀减速直线运动,则v1<v2
4.初速度为零的匀加速直线运动的几个比例关系(T为单位时间)。
(1)1T末、2T末、3T末…的速度之比:
v1∶v2∶v3∶…∶vn=1∶2∶3∶…∶n。
(2)1T内、2T内、3T内…的位移之比:
s1∶s2∶s3∶…∶sn=1∶22∶33∶…∶n2。
(3)第一个T内、第二个T内、第三个T内…的位移之比:
sⅠ∶sⅡ∶sⅢ∶…∶sN=1∶3∶5∶…∶(2N-1)。
(4)通过连续相等的位移所用的时间之比:
t1∶t2∶t3∶…∶tn=1∶(-1)∶(-)∶…∶(-)。
(5)通过前1
s、前2
s、前3
s…的位移所用的时间之比:
tⅠ∶tⅡ∶tⅢ∶…∶tN=1∶∶∶…∶。
5.末速度为零的匀减速直线运动
对于末速度为零的匀减速直线运动,可以按逆过程分析,视为初速度为零的匀加速直线运动,运用前面的比例关系,使运算大为简化。
【例3】一小球沿斜面由静止开始匀加速滚下(斜面足够长),已知小球在第4
s末的速度为4
m/s。求:
(1)第6
s末的速度;
(2)前6
s内的位移;
(3)第6
s内的位移。
解析:由v1=at1,得a===1
m/s2
所以第1
s内的位移s1=a×12
m=0.5
m。
(1)由于第4
s末与第6
s末的速度之比
v1∶v2=4∶6=2∶3,
故第6
s末的速度v2=v1=6
m/s。
(2)第1
s内与前6
s内的位移之比s1∶s6=12∶62
故前6
s内小球的位移s6=36s1=18
m。
(3)第1
s内与第6
s内的位移之比
sⅠ∶sⅥ=1∶(2×6-1),
故第6
s内的位移sⅥ=11sⅠ=5.5
m。
答案:(1)6
m/s (2)18
m (3)5.5
m
求例题中的小球
(1)在前6
s内的平均速度(采用多种求法);
(2)在第6
s内的平均速度(采用多种求法)。
答案:(1)3
m/s (2)5.5
m/s
3-1物体由静止开始做匀加速直线运动,前三个连续时间段的时间之比为1∶2∶3,该三段位移之比为多少?平均速度之比为多少?
三、刹车类交通工具的匀减速直线运动的处理
1.特点:对于汽车刹车、飞机降落后在跑道上滑行等这类交通工具的匀减速直线运动,当速度减到零后,加速度也为零,不可能倒过来做反向的运动,所以其运动的最长时间t=。
2.处理方法:首先计算速度减到零所需时间,然后再与题中所给的时间比较,看在所给的时间内是否早已停止,如果是,则不能用题目所给的时间计算,这就是所谓的“时间过量”问题;如果没有停止,则可以应用题目所给的时间直接求解。
【例4】(2012·江西南昌检测)一辆汽车以36
km/s的速度行驶在城市的街道上,因为前方路口出现红灯,司机从较远的地方开始刹车,刹车后的加速度大小为5
m/s2,求:
(1)刹车1
s后汽车的速度;
(2)刹车多长时间后汽车停下;
(3)刹车4
s后汽车的速度。
解析:汽车刹车后做匀减速直线运动,加速度方向和初速度方向相反,速度取正值时,加速度取负值。
且知:v0=36
km/h=10
m/s,a=-5
m/s2
(1)t1=1
s时,v1=v0+at1=10
m/s-5×1
m/s=5
m/s
(2)由v=v0+at知t==
s=2
s
(3)因刹车2
s后汽车就已经停下,所以4
s时速度为0。
答案:(1)5
m/s (2)2
s (3)0
生活中的现象告诉我们汽车刹车停下时不再运动,所以对于刹车及类似刹车问题,为防止因盲目套用公式出错,应先计算刹车时间,根据给出时间与刹车时间的关系,确定计算的方法。
4-1磁悬浮列车由静止开始加速出站,加速度为0.6
m/s2,2
min后列车速度为多大?列车匀速运动时速度为432
km/h,如果以0.8
m/s2的加速度减速进站,求减速160
s时速度为多大?
答案:
【互动课堂】
迁移训练
1-1 D 解析:因题中只给出初、末时刻速度的大小,这就隐含着初、末速度方向可能相同也可能相反的两种情况,故需讨论。若初、末速度方向相同,物体做匀加速直线运动,加速度a1=
m/s2=2
m/s2;若初、末速度方向相反,物体做匀减速直线运动,加速度a2=
m/s2=-6
m/s2,负号表示加速度的方向与v0方向相反。
1-2 AC 解析:v-t图象的斜率表示加速度,故A正确,D不正确;s-t图象的斜率表示速度,故B不正确;匀变速直线运动,加速度恒定,故C正确。
2-1 解析:做匀变速直线运动的物体,在某段时间内的平均速度等于该段时间的中间时刻的瞬时速度,
即==
2.5
s时刻的速度为v1:
v1=第3秒内=15
m/s
8.5
s时刻的速度为v2:
v2=第9秒内=9
m/s
加速度a==
m/s2=-1
m/s2。
答案:-1
m/s2
2-2 AB 解析:若做匀加速直线运动,则由v-t图象知v1>v2
若做匀减速直线运动的v-t图象如下图所示,由图象知v1>v2。
3-1 解析:由题意可将运动时间分割成6等份,每份为t,根据初速度为零的匀加速直线运动在连续相等时间内的位移之比s1∶s2∶s3∶s4∶s5∶s6=1∶3∶5∶7∶9∶11可知st∶s2t∶s3t=1∶(3+5)∶(7+9+11)=1∶8∶27。由=得t∶2t∶3t=∶∶=∶∶=1∶4∶9。
速度之比也可以通过以下方法求得:
第1个t末的速度v1=a·t
第3个t末的速度v2=a·3t
第6个t末的速度v3=a·6t
故三段平均速度之比为vt∶v2t∶v3t
=∶∶=1∶4∶9。
答案:1∶8∶27 1∶4∶9
4-1 解析:取列车运动方向为正方向。
v=v10+a1t1=(0+0.6×120)m/s=72
m/s=259
km/h。
列车减速进站时a2=-0.8
m/s2
v20=432
km/h=120
m/s
刹车到速度为0的时间t0==
s=150
s
所以160
s时列车已经停止运动,速度为0。
答案:259
km/h 0
一、匀变速直线运动的基本规律
1.匀变速直线运动的特点:加速度a恒定且轨迹为直线。
2.匀变速直线运动的基本公式
(1)速度—时间公式:vt=v0+at。
(2)位移—时间公式:s=v0t+at2。
(3)位移—速度—加速度公式2as=v-v。
你知道上述公式是怎样推得的吗?
答案:由a==得vt=v0+at
由s=t=·t得s=v0t+at2
或由v-t图象推导,由图象与横轴所构成面积求得
s梯形=s=v0t+at2
将速度中的t代入位移公式得2as=v-v。
3.匀变速直线运动的图象描述
如图所示甲图中甲、乙的加速度有何关系?丙一直做匀变速运动吗?
答案:甲、乙的加速度相等,因为图象平行,图象的斜率表示加速度,所以甲、乙加速度相同;同理丙一直做匀变速直线运动,t1时刻前a<0,v0>0,做匀减速直线运动,t1时刻后a<0,v<0,做反方向匀加速直线运动。
【例1】如图所示,小球以6
m/s的速度由足够长的斜面中部沿着斜面向上滑。已知小球在斜面上运动的加速度大小为2
m/s2,则小球的速度大小何时达到3
m/s?(小球在光滑斜面上运动时,加速度的大小、方向都不改变)
解析:小球先沿斜面向上做匀减速直线运动,速度由6
m/s逐渐减小到零,然后又反向做匀加速直线运动。取沿斜面向上的方向为正方向,则v0=6
m/s,a=-2
m/s2,小球的速度大小为3
m/s有两种情况:向上滑时v1=3
m/s,向下滑时v2=-3
m/s。由公式v=v0+at得t=,所以t1==
s=1.5
s,t2==
s=4.5
s。
答案:1.5
s或4.5
s
在审题时,应格外关注以下词语:“速度大小达到3
m/s”,说明只确定了大小,没确定方向,方向分两种情况讨论。
1-1某物体做匀变速直线运动,某时刻速度的大小为4
m/s,2
s后速度的大小变为8
m/s,在这2
s内物体的( )
A.加速度方向与初速度方向相同
B.加速度方向与末速度方向相同
C.加速度的大小可能小于2
m/s2
D.加速度的大小可能大于4
m/s2
1-2(2012·山东东营质检)下列图象能表示匀变速直线运动的是( )
二、匀变速直线运动的几个重要推论
1.平均速度等于速度平均,等于中间时刻的速度,即==v。
2.中间位置的速度:=
3.逐差相等:s2-s1=s3-s2=…=sn-sn-1=aT2
设在任意连续相等时间间隔T内的位移分别为s1、s2、s3、…,则
s1=v0T+aT2
s2=(v0+aT)T+aT2
s3=(v0+aT+aT)T+aT2
sn=[v0+(n-1)aT]T+aT2
于是有s2-s1=s3-s2=…=sn-sn-1=aT2,即Δs=aT2,任意相邻两个连续相等的时间里的位移之差是一个恒量。该结论常作为判断一个运动是否是匀变速直线运动的依据。
【例2】某市规定,车辆在市区内行驶的速度不得超过40
km/h,有一辆车遇到紧急情况而刹车(刹车后该车做匀减速运动),经1.5
s停止,量得路面刹车的痕迹长为s=9
m,问这辆车是否违章?
解析:本题隐含了末速度为零的条件,因此只需求出初速度就可以判定。
由于汽车刹车后做匀减速运动,则平均速度=,又因为位移s=t,所以s=t,解得v0==12
m/s=43.2
km/h>40
km/h。
因此该辆车违章行驶。
答案:该辆车违章行驶。
2-1某物体做匀变速直线运动,其在第3
s内发生15
m的位移,在第9
s内发生9
m的位移,问其加速度为多大?
2-2做匀变速直线运动的物体先后通过A、B两点,通过A、B点的瞬时速度分别为vA和vB.若物体通过A、B连线中点C的瞬时速度为v1,通过A到B所用时间中间时刻的瞬时速度为v2,关于v1、v2的大小,下列说法正确的是( )
A.若做匀加速直线运动,则v1>v2
B.若做匀减速直线运动,则v1>v2
C.若做匀加速直线运动,则v1<v2
D.若做匀减速直线运动,则v1<v2
4.初速度为零的匀加速直线运动的几个比例关系(T为单位时间)。
(1)1T末、2T末、3T末…的速度之比:
v1∶v2∶v3∶…∶vn=1∶2∶3∶…∶n。
(2)1T内、2T内、3T内…的位移之比:
s1∶s2∶s3∶…∶sn=1∶22∶33∶…∶n2。
(3)第一个T内、第二个T内、第三个T内…的位移之比:
sⅠ∶sⅡ∶sⅢ∶…∶sN=1∶3∶5∶…∶(2N-1)。
(4)通过连续相等的位移所用的时间之比:
t1∶t2∶t3∶…∶tn=1∶(-1)∶(-)∶…∶(-)。
(5)通过前1
s、前2
s、前3
s…的位移所用的时间之比:
tⅠ∶tⅡ∶tⅢ∶…∶tN=1∶∶∶…∶。
5.末速度为零的匀减速直线运动
对于末速度为零的匀减速直线运动,可以按逆过程分析,视为初速度为零的匀加速直线运动,运用前面的比例关系,使运算大为简化。
【例3】一小球沿斜面由静止开始匀加速滚下(斜面足够长),已知小球在第4
s末的速度为4
m/s。求:
(1)第6
s末的速度;
(2)前6
s内的位移;
(3)第6
s内的位移。
解析:由v1=at1,得a===1
m/s2
所以第1
s内的位移s1=a×12
m=0.5
m。
(1)由于第4
s末与第6
s末的速度之比
v1∶v2=4∶6=2∶3,
故第6
s末的速度v2=v1=6
m/s。
(2)第1
s内与前6
s内的位移之比s1∶s6=12∶62
故前6
s内小球的位移s6=36s1=18
m。
(3)第1
s内与第6
s内的位移之比
sⅠ∶sⅥ=1∶(2×6-1),
故第6
s内的位移sⅥ=11sⅠ=5.5
m。
答案:(1)6
m/s (2)18
m (3)5.5
m
求例题中的小球
(1)在前6
s内的平均速度(采用多种求法);
(2)在第6
s内的平均速度(采用多种求法)。
答案:(1)3
m/s (2)5.5
m/s
3-1物体由静止开始做匀加速直线运动,前三个连续时间段的时间之比为1∶2∶3,该三段位移之比为多少?平均速度之比为多少?
三、刹车类交通工具的匀减速直线运动的处理
1.特点:对于汽车刹车、飞机降落后在跑道上滑行等这类交通工具的匀减速直线运动,当速度减到零后,加速度也为零,不可能倒过来做反向的运动,所以其运动的最长时间t=。
2.处理方法:首先计算速度减到零所需时间,然后再与题中所给的时间比较,看在所给的时间内是否早已停止,如果是,则不能用题目所给的时间计算,这就是所谓的“时间过量”问题;如果没有停止,则可以应用题目所给的时间直接求解。
【例4】(2012·江西南昌检测)一辆汽车以36
km/s的速度行驶在城市的街道上,因为前方路口出现红灯,司机从较远的地方开始刹车,刹车后的加速度大小为5
m/s2,求:
(1)刹车1
s后汽车的速度;
(2)刹车多长时间后汽车停下;
(3)刹车4
s后汽车的速度。
解析:汽车刹车后做匀减速直线运动,加速度方向和初速度方向相反,速度取正值时,加速度取负值。
且知:v0=36
km/h=10
m/s,a=-5
m/s2
(1)t1=1
s时,v1=v0+at1=10
m/s-5×1
m/s=5
m/s
(2)由v=v0+at知t==
s=2
s
(3)因刹车2
s后汽车就已经停下,所以4
s时速度为0。
答案:(1)5
m/s (2)2
s (3)0
生活中的现象告诉我们汽车刹车停下时不再运动,所以对于刹车及类似刹车问题,为防止因盲目套用公式出错,应先计算刹车时间,根据给出时间与刹车时间的关系,确定计算的方法。
4-1磁悬浮列车由静止开始加速出站,加速度为0.6
m/s2,2
min后列车速度为多大?列车匀速运动时速度为432
km/h,如果以0.8
m/s2的加速度减速进站,求减速160
s时速度为多大?
答案:
【互动课堂】
迁移训练
1-1 D 解析:因题中只给出初、末时刻速度的大小,这就隐含着初、末速度方向可能相同也可能相反的两种情况,故需讨论。若初、末速度方向相同,物体做匀加速直线运动,加速度a1=
m/s2=2
m/s2;若初、末速度方向相反,物体做匀减速直线运动,加速度a2=
m/s2=-6
m/s2,负号表示加速度的方向与v0方向相反。
1-2 AC 解析:v-t图象的斜率表示加速度,故A正确,D不正确;s-t图象的斜率表示速度,故B不正确;匀变速直线运动,加速度恒定,故C正确。
2-1 解析:做匀变速直线运动的物体,在某段时间内的平均速度等于该段时间的中间时刻的瞬时速度,
即==
2.5
s时刻的速度为v1:
v1=第3秒内=15
m/s
8.5
s时刻的速度为v2:
v2=第9秒内=9
m/s
加速度a==
m/s2=-1
m/s2。
答案:-1
m/s2
2-2 AB 解析:若做匀加速直线运动,则由v-t图象知v1>v2
若做匀减速直线运动的v-t图象如下图所示,由图象知v1>v2。
3-1 解析:由题意可将运动时间分割成6等份,每份为t,根据初速度为零的匀加速直线运动在连续相等时间内的位移之比s1∶s2∶s3∶s4∶s5∶s6=1∶3∶5∶7∶9∶11可知st∶s2t∶s3t=1∶(3+5)∶(7+9+11)=1∶8∶27。由=得t∶2t∶3t=∶∶=∶∶=1∶4∶9。
速度之比也可以通过以下方法求得:
第1个t末的速度v1=a·t
第3个t末的速度v2=a·3t
第6个t末的速度v3=a·6t
故三段平均速度之比为vt∶v2t∶v3t
=∶∶=1∶4∶9。
答案:1∶8∶27 1∶4∶9
4-1 解析:取列车运动方向为正方向。
v=v10+a1t1=(0+0.6×120)m/s=72
m/s=259
km/h。
列车减速进站时a2=-0.8
m/s2
v20=432
km/h=120
m/s
刹车到速度为0的时间t0==
s=150
s
所以160
s时列车已经停止运动,速度为0。
答案:259
km/h 0
同课章节目录
- 第1章 绪论
- 物理学与自然规律
- 物理学与社会发展
- 怎样学习物理学
- 高中物理教材特点
- 第2章 运动的描述
- 导入 认识运动
- 第1节 运动、空间和时间
- 第2节 质点和位移
- 第3节 速度和加速度
- 第3章 匀变速直线运动的研究
- 导入 速度的变化
- 第1节 匀变速直线运动的规律
- 第2节 匀变速直线运动的实验探究
- 第3节 匀变速直线运动实例-自由落体运动
- 第4章 相互作用
- 导入 奇特的力现象
- 第1节 重力与重心
- 第2节 形变与弹力
- 第3节 摩擦力
- 第5章 力与平衡
- 导入 感悟平衡之美
- 第1节 力的合成
- 第2节 力的分解
- 第3节 力的平衡
- 第4节 平衡条件的应用
- 第6章 力与运动
- 导入 跨越时空的对话
- 第1节 牛顿第一定律
- 第2节 牛顿第二定律
- 第3节 牛顿第三定律
- 第4节 超重与失重
- 本章复习与测试
