4.1 重力与重心 课件 (3)

课件37张PPT。第1节 重力与重心温故知新1．力的________、________、________称为力的三要素．
(1)力的图示：用带箭头的线段表示力，它的长短表示力的________，它的指向表示力的_______，箭头(或箭尾)表示力的________．
(2)力的示意图：只需画出力的________和________，表示物体在这个方向上受到了力．
答案：大小　方向　作用点　(1)大小　方向　作用点　(2)作用点　方向
精彩回眸2．重力是由于物体________而产生的．重力的大小G＝________，重力的方向________，重力在物体上的________叫重心．
答案：受到地球的吸引　mg　竖直向下　作用点
1．力的描述
(1)力是物体与物体之间的_____作用，是使物体的形状和运动状态发生改变的原因．
(2)力是矢量：既有____又有____ ．力的大小可以用______测量，在国际单位制中，力的单位是___，简称牛，符号N.
新知梳理相互大小方向牛测力计顿(3)力的图示：用一带箭头的有向线段表示力的____和____，线段是按一定的比例(标度)画出的，它的____表示力的大小．
(4)力的示意图：用一带箭头的有向线段表示力的______和____，只表明物体在这个______受到了力，______不严格表示力的大小．
(5)自然界存在的四种基本相互作用是：________作用、________作用、强相互作用、弱相互作用．
作用点方向长短作用点方向方向上线段长短万有引力电磁相互2．重力及其测量
(1)定义：由于地球的____而使物体受到的力．
(2)公式：G＝___.
(3)方向：总是_________．
重力的施力物体是地球，地球周围的物体都受重力作用．
重力的方向竖直向下，不能理解成垂直于地面向下．
吸引mg竖直向下3．重心与稳定
(1)物体的各部分都受____作用，从效果上看，可认为各个部分受到的重力作用集中于一点，即为物体的____．
(2)重心的位置：a.与物体的____有关；b.与物体内____的分布有关．
(3)薄板形物体的重心位置的确定方法：悬挂法．形状规则、质量分布均匀的物体的重心在其几何中心上．
重力重心形状质量合作探究1．对力的概念的理解
(1)相互性：力的作用是相互的，一个物体对另一个物体施加了力，另一个物体也必然同时对该物体施加力的作用．
(2)物质性：力不能脱离物体而独立存在．
(3)力的矢量性：力有方向，描述一个力既要说明大小，还要指明方向．
力和力的图示
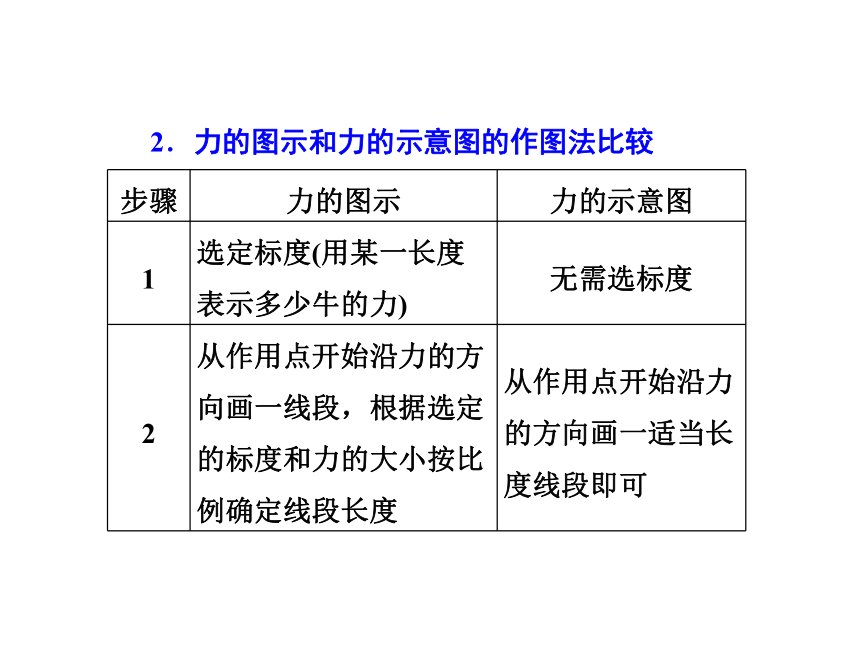
2．力的图示和力的示意图的作图法比较
特别提醒：(1)用力的图示法表示力时，标度的选取是任意的，实际作图时可根据力的大小选取恰当的标度．
(2)在同一物体上画几个力的图示时，所选取的标度应当统一．
1. 如图4－1－1所示，物体A对物体B的压力是10 N，试画出这个力的图示和示意图．
图4－1－1解析：画力的图示(1)选定标度：此题选2 mm长的线段表示2 N的力．
(2)从作用点沿力的方向画一线段，线段长短根据选定的标度和力的大小成正比，线段上加刻度，如图甲所示，也可以如图乙所示，从O点(用O点代替B物体)竖直向下画一段五倍于标度(10 mm)的线段；
(3)在线段上加箭头表示力的方向．
画力的示意图：从作用点或从B的中心处沿力的方向画一线段，并加上箭头，表示方向，然后标明N＝10 N即可，如图丙所示．
答案：见解析
1．重力
(1)大小：G＝mg.
①在同一地点，重力的大小与质量成正比．
②在不同地点，重力的大小与物体所处的纬度位置有关，在纬度越高的位置，所受重力越大；重力的大小还与物体的海拔高度有关，在同一纬度，位置越高，重力越小．
③重力的大小与物体的运动状态无关，与物体是否受其他力无关．重力及重力的测量
(2)方向：总是竖直向下，而不是垂直向下．
2．重力的测量
(1)测量工具：弹簧测力计．
(2)测量方法：竖直悬挂在测力计上的物体静止时，测力计的示数即为物体重力的大小．
特别提醒：(1)重力是由于地球的吸引而产生，但重力的大小不一定等于地球对物体的吸引力，重力的方向不一定指向地心．
(2)由于重力的方向竖直向下，地球是一个球体，所以物体在地球表面不同的位置时所受重力的方向一般不同．
(3)物体的重力随g值的变化而变化，而g值随纬度的增加而增大，在同一纬度g值随高度的增加而减小．
2．关于重力的大小，下列说法中正确的是(　　)
A．物体的重力大小总是恒定的
B．同一地点，物体的重力与物体的质量成正比
C．物体落向地面时，它受到的重力大于它静止时所受到的重力
D．物体的重力总等于它对竖直弹簧测力计的拉力
解析：物体的重力的计算公式为G＝mg，物体的质量m是恒定的，但g的取值与地理位置有关．对同一地点，g的取值相同，随高度的增大g值将减小．随着物体所处的地理位置的纬度的增大，g值将增大．故A错误、B正确；由公式可知，物体所受的重力只与物体的质量及g值有关，与物体是否受其他力及运动状态均无关，故C错误；用弹簧测力计竖直悬挂重物在静止或匀速直线运动时，物体对弹簧测力计的拉力才等于其重力，故D错误．
答案：B
重心与稳定
1．对重心的理解
(1)重心并不是实际存在的一个特殊点，它的位置跟物体的形状和物体的各部分的质量有关．
(2)对于质量分布均匀的物体，重心的位置只跟物体的形状有关，若形状规则，物体的重心在几何中心上．例如，均匀细直棒的重心在棒的中点，均匀球体的重心在球心．
(3)质量分布不均匀的物体，重心的位置除了跟物体的形状有关外，还跟物体内质量分布有关．例如，载重车辆重心随着货物多少和装载位置而变化，起重机的重心随着提升物的重量和高度而变化．
(4)重心的位置并不一定都位于物体上．例如，我们平时玩的篮球、排球、圆环等物体的重心位置是在球心或圆心上．
2．悬挂法测重心
(1)条件：薄板状物体．
(2)原理：当悬挂的物体静止时，重力和拉力作用在同一条直线上，重心一定位于过悬挂点的竖直线上．
3．重心的高低对物体稳定性的影响
(1)物体的稳定性往往受重心高度的影响，物体的重心越低，则物体越稳定，生活中往往采用降低重心高度的办法来增加物体的稳定性，如装运货物时，往往把较重的货物放在下面，就是为了降低重心，增大稳定性．
(2)当物体的重力作用线落在它的支持面内时，物体可以保持稳定，落到支持面外时则会倾斜，如车辆行驶时车身倾斜的角度不能过大．
3．关于物体的重心，下列说法正确的是(　　)
A．任何有规则形状的物体，它的重心一定与它的几何中心重合
B．用一根绳子将物体悬挂，物体处于静止状态，该物体的重心一定在悬绳的延长线上
C．任何物体的重心都必须在物体上
D．有固定形状的物体重心相对于物体的位置，不因物体升高、降低或倾斜而发生变化
解析：有规则几何外形且必须质量分布均匀的物体重心才一定在几何中心上，A错误；用悬挂法确定物体重心时，两次悬挂时悬绳的延长线的交点即为重心位置，B对；有些物体(比如圆环)的重心不在物体本身上，C错；形状固定的物体，重心的位置相对物体本身不变，D对．
答案：BD
典例精析力的性质和力的图示【典例1】 下列说法正确的是 (　　)
A．用手压弹簧，手给弹簧一个作用力，弹簧对手没有作用力
B．运动员将垒球抛出后，垒球的运动状态仍在变化，垒球仍为受力物体，但施力物体不是运动员
C．施力物体对受力物体施加了力，施力物体本身可能不受力的作用
D．某物体作为一个施力物体，也一定是受力物体
思路分析：解答本题的关键要理解力的概念，即力是物体之间的相互作用．
解析：力的作用具有相互性，即物体甲对乙有力的作用的同时，乙对甲也有力的作用，因此选项A、C错，D正确；垒球在运动过程中，已脱离了运动员的作用，但必受重力和空气阻力的作用，因此运动状态发生了变化，故选项B正确．
答案：BD
反思领悟：物体之间力的作用是相互的，每个物体都既是施力物体，也是受力物体．物体的运动状态发生改变时，一定是由于受到了力的作用．另外，为了能够在解题中表示力，必须学会力的图示．
如图4－1－2所示，一木箱放置在水平桌面上，桌面对它的支持力是20 N．画出这个力的图示．
图4－1－2解析：①取标度，如右图所示，选取5 mm长的线段表示5 N的力．
②从力的作用点O沿垂直桌面方向向上画一线段，线段长度4倍于标度，即取20 mm长，并在线段上加标度．
③在线段上端端点加上箭头表示力的方向．
答案：见解析
重力与重心【典例2】 下列说法正确的是 (　　)
A．形状规则的物体的重心，一定在物体的几何中心上
B．物体的重心一定在其内部
C．地球对物体的吸引力就是物体的重力
D．物体的重力，是由于地球对物体的吸引而产生的
思路分析：解答本题的关键是要正确理解重力和重心的概念．
解析：物体重心的位置不但与物体的形状有关，还和物体质量分布情况有关，所以选项A错；物体的重心不一定在物体上，如质量分布均匀的圆环的重心在其圆心，但不在圆环上，故选项B错；重力是由于物体受到地球的吸引而产生的，但地球对物体的吸引力并不是重力，故选项C错，D对．
答案：D
反思领悟：影响物体重心位置的因素有物体的形状和物体的质量分布，重心可以在物体上，也可以在物体之外．重力的施力物体是地球，但重力和地球对物体的吸引力是有差异的．
一个重为20 N的物体沿着斜面下滑，在下图中，关于物体所受重力的图示正确的是(　　)
解析：作力的图示的时候，箭尾应在力的作用点上；箭头指向为力的方向；根据选定标度表示力的大小，箭头应画在线段的末端；重力方向总是竖直向下的．
答案：A
重心的确定方法
重心是一个等效作用点，引入重心的概念后，整个物体就可以用一个有质量的点来代替，从而使研究问题大大简化．要注意重心并非物体上最重的点，也并非只有这一点才受到重力的作用．确定物体重心的位置要注意物体的形状和质量的分布情况．薄板的重心位置可以用悬挂法求出，对于复杂的物体系统，其重心可以采用由局部到全局的计算方法求出．
创新拓展【典例3】 如图4－1－3所示，有一等边三角形ABC，在B、C两点各放一个质量为m的小球，在A点放一个质量为2m的小球，则这个球组的重心在何处？
图4－1－3思路分析：要求一个系统的重心位置，可以把这个系统分成几部分，从最方便处着手，逐步找出重心的位置．
解析：根据题意可先求出B、C两球的重心，即在B、C连线的中点处．可以认为在B、C连线的中点处有一个质量为2m的小球D，如右图所示，接着求A、D两球的重心，因为A、D两球质量相等，所以其重心位于A、D两点连线的中点E处．
答案：重心位于BC的中点与A点连线的中点处