4.2 形变与弹力 同步练习(含答案解析) (1)
文档属性
| 名称 | 4.2 形变与弹力 同步练习(含答案解析) (1) |  | |
| 格式 | zip | ||
| 文件大小 | 449.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-08-13 14:11:40 | ||
图片预览


文档简介
4.2
形变与弹力
同步练习
1.下列说法中不正确的是( )
A.书放在水平桌面上受到的支持力,是由于书发生了微小形变而产生的
B.用细木棍拨动浮在水中的圆木,圆木受到的弹力是由于细木棍发生形变而产生的
C.绳对物体的拉力方向总是沿着绳而指向绳收缩的方向
D.支持力的方向总是垂直于支持面而指向被支持的物体
【解析】 弹力是发生弹性形变的物体对对方施加的力,书放在水平桌面上受到的支持力,是由于桌面发生了微小形变而产生的.A不正确,B正确.弹力的方向垂直于接触面而指向受力物体,绳类柔软物体的弹力方向指向收缩的方向,C、D正确.故选A.
【答案】 A
2.关于形变和弹力的说法中,正确的是( )
A.相互接触的物体先产生形变后产生弹力
B.相互接触的物体先产生弹力后产生形变
C.相互接触的物体产生形变的同时产生弹力
D.
物体间弹力的作用不是相互的
【解析】 相互接触的物体产生形变的同时也就产生了弹力,二者无先后之分,A、B错误,C正确,物体间任何力的作用都是相互的,D错.
【答案】 C
3.下列两个实验中体现出的共同的物理思想方法是( )
图4-2-13
A.极限法
B.放大法
C.控制变量法
D.等效替代法
【解析】 图甲是利用光的反射将微小形变放大,图乙是利用细管中液面的变化观察玻璃瓶的微小形变,故为放大法,B正确.
【答案】 B
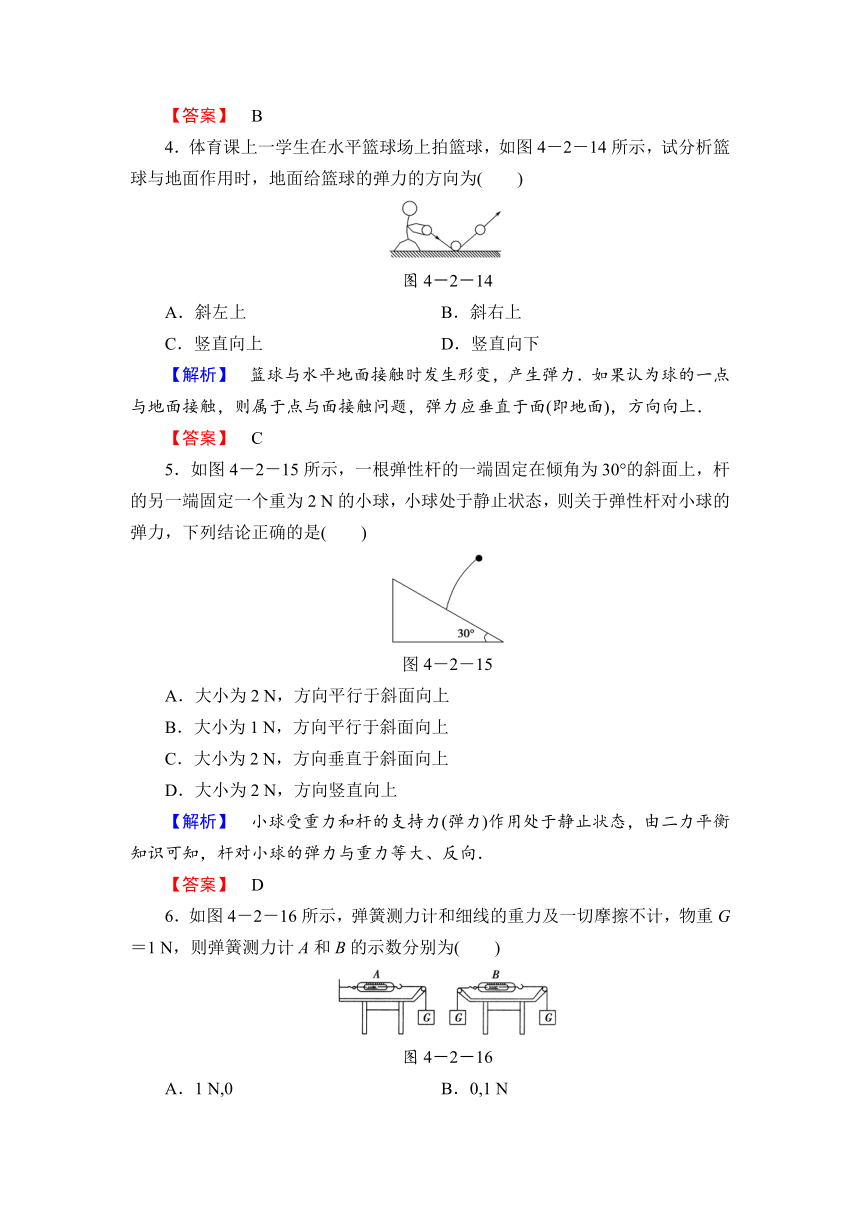
4.体育课上一学生在水平篮球场上拍篮球,如图4-2-14所示,试分析篮球与地面作用时,地面给篮球的弹力的方向为( )
图4-2-14
A.斜左上
B.斜右上
C.竖直向上
D.竖直向下
【解析】 篮球与水平地面接触时发生形变,产生弹力.如果认为球的一点与地面接触,则属于点与面接触问题,弹力应垂直于面(即地面),方向向上.
【答案】 C
5.如图4-2-15所示,一根弹性杆的一端固定在倾角为30°的斜面上,杆的另一端固定一个重为2
N的小球,小球处于静止状态,则关于弹性杆对小球的弹力,下列结论正确的是( )
图4-2-15
A.大小为2
N,方向平行于斜面向上
B.大小为1
N,方向平行于斜面向上
C.大小为2
N,方向垂直于斜面向上
D.大小为2
N,方向竖直向上
【解析】 小球受重力和杆的支持力(弹力)作用处于静止状态,由二力平衡知识可知,杆对小球的弹力与重力等大、反向.
【答案】 D
6.如图4-2-16所示,弹簧测力计和细线的重力及一切摩擦不计,物重G=1
N,则弹簧测力计A和B的示数分别为( )
图4-2-16
A.1
N,0
B.0,1
N
C.2
N,1
N
D.1
N,1
N
【解析】 弹簧测力计的示数等于钩受到的拉力,与弹簧测力计外壳受力无关,物体平衡时绳对物体的拉力F与物重G是一对平衡力,所以F=G=1
N.两弹簧测力计的读数都为1
N,所以D正确.
【答案】 D
7.如图4-2-17所示,弹簧的劲度系数为k,小球重力为G,平衡时球在A位置,今用力F将小球向下拉长x至B位置,则此时弹簧的弹力为( )
图4-2-17
A.kx
B.kx+G
C.G-kx
D.以上都不对
【解析】 对此题,x不是弹簧形变后的长度与不发生形变的长度的差值.球在A位置时弹簧已经伸长了(令它为Δx),这样FB=k(Δx+x)=kΔx+kx.球在A位置平衡时有G=kΔx,所以FB=kx+G,故选项B是正确的.
【答案】 B
8.如图4-2-18所示,物块A静止在斜面B上,下列说法正确的是( )
图4-2-18
A.斜面B对物块A的弹力方向是竖直向上的
B.物块A对斜面B的弹力方向是竖直向下的
C.斜面B对物块A的弹力方向是垂直斜面向上的
D.物块A对斜面B的弹力方向跟物块A恢复形变的方向是相反的
【解析】 斜面B对物块A的弹力方向垂直于斜面向上,A错,C对.物块A对斜面B的弹力方向垂直于斜面向下,跟物块A恢复形变的方向是相同的,B、D错.
【答案】 C
9.一根轻质弹簧一端固定,用大小为F1的力压弹簧的另一端,平衡时长度为l1;改用大小为F2的力拉弹簧,平衡时长度为l2.弹簧的拉伸和压缩均在弹性限度内,该弹簧的劲度系数为( )
A.
B.
C.
D.
【解析】 设弹簧的原长为l,劲度系数为k,由胡克定律F=kx得,F1=k(l-l1),F2=k(l2-l),联立两式求得k=,C正确.
【答案】 C
10.如图4-2-19所示,四个完全相同的弹簧都处于水平位置,它们的右端受到大小皆为F的拉力作用,而左端的情况各不相同:①中弹簧的左端固定在墙上;②中弹簧的左端受大小也为F的拉力作用;③中弹簧的左端拴一小物块,物块在光滑的桌面上滑动;④中弹簧的左端拴一小物块,物块在粗糙的桌面上滑动.若认为弹簧的质量都为零,以l1、l2、l3、l4依次表示四个弹簧的伸长量,则有( )
图4-2-19
A.l1>l2
B.l2>l3
C.l3>l4
D.l1=l2=l3=l4
【解析】 本题考查弹簧所受拉力与弹簧伸长量的关系.弹簧的伸长量等于弹簧弹力与弹簧劲度系数的比值,分析四种情况下弹簧所受弹力都等于外力F,又因弹簧完全相同,劲度系数相同,所以四种情况下弹簧的伸长量相等.
【答案】 D
11.某人设计了一只弹簧测力计,如图4-2-20所示,当弹簧的自由端B未悬挂重物时指针正对刻度5,在弹性限度内,当挂上80
N重物时指针正对刻度45;当指针正对刻度20时,请你探究分析所挂重物的重量为多少?
图4-2-20
【解析】 弹簧的伸长量可用刻度的变化量表示.当所挂重物G1=80
N时,伸长量x1=40;当指针正对刻度20时,弹簧伸长量x2=15.设所挂重物为G2,根据二力平衡和胡克定律得,G1=kx1,G2=kx2,所以G2=G1=×80
N=30
N.
【答案】 30
N
12.
“蹦极”是一种非常刺激的户外休闲运动,人从水面上方某处的平台上跳下,靠自身所受的重力让其自由下落,被拉伸的橡皮绳又会产生向上的力,把人拉上去,然后人再下落.正是在这上上下下的运动中,蹦极者体会到惊心动魄的刺激,如图4-2-21所示.设一次蹦极中所用的橡皮绳原长为15
m.质量为50
kg的人在下落到最低点时所受的向上的最大拉力为3
000
N,已知此人停在空中时,蹦极的橡皮绳长度为17.5
m,橡皮绳的弹力与伸长的关系符合胡克定律.(取g=10
N/kg).求:
图4-2-21
(1)橡皮绳的劲度系数;
(2)橡皮绳的上端悬点离下方的水面至少为多高?
【解析】 (1)人静止于空中时,橡皮绳的拉力F1=500
N.
而F1=k(l-l0),所以橡皮绳劲度系数k==
N/m=200
N/m.
(2)设橡皮绳拉力最大时,绳长为l′.
据胡克定律F2=k(l′-l0)得
l′=+l0=
m+15
m=30
m.
【答案】 (1)200
N/m (2)30
m
形变与弹力
同步练习
1.下列说法中不正确的是( )
A.书放在水平桌面上受到的支持力,是由于书发生了微小形变而产生的
B.用细木棍拨动浮在水中的圆木,圆木受到的弹力是由于细木棍发生形变而产生的
C.绳对物体的拉力方向总是沿着绳而指向绳收缩的方向
D.支持力的方向总是垂直于支持面而指向被支持的物体
【解析】 弹力是发生弹性形变的物体对对方施加的力,书放在水平桌面上受到的支持力,是由于桌面发生了微小形变而产生的.A不正确,B正确.弹力的方向垂直于接触面而指向受力物体,绳类柔软物体的弹力方向指向收缩的方向,C、D正确.故选A.
【答案】 A
2.关于形变和弹力的说法中,正确的是( )
A.相互接触的物体先产生形变后产生弹力
B.相互接触的物体先产生弹力后产生形变
C.相互接触的物体产生形变的同时产生弹力
D.
物体间弹力的作用不是相互的
【解析】 相互接触的物体产生形变的同时也就产生了弹力,二者无先后之分,A、B错误,C正确,物体间任何力的作用都是相互的,D错.
【答案】 C
3.下列两个实验中体现出的共同的物理思想方法是( )
图4-2-13
A.极限法
B.放大法
C.控制变量法
D.等效替代法
【解析】 图甲是利用光的反射将微小形变放大,图乙是利用细管中液面的变化观察玻璃瓶的微小形变,故为放大法,B正确.
【答案】 B
4.体育课上一学生在水平篮球场上拍篮球,如图4-2-14所示,试分析篮球与地面作用时,地面给篮球的弹力的方向为( )
图4-2-14
A.斜左上
B.斜右上
C.竖直向上
D.竖直向下
【解析】 篮球与水平地面接触时发生形变,产生弹力.如果认为球的一点与地面接触,则属于点与面接触问题,弹力应垂直于面(即地面),方向向上.
【答案】 C
5.如图4-2-15所示,一根弹性杆的一端固定在倾角为30°的斜面上,杆的另一端固定一个重为2
N的小球,小球处于静止状态,则关于弹性杆对小球的弹力,下列结论正确的是( )
图4-2-15
A.大小为2
N,方向平行于斜面向上
B.大小为1
N,方向平行于斜面向上
C.大小为2
N,方向垂直于斜面向上
D.大小为2
N,方向竖直向上
【解析】 小球受重力和杆的支持力(弹力)作用处于静止状态,由二力平衡知识可知,杆对小球的弹力与重力等大、反向.
【答案】 D
6.如图4-2-16所示,弹簧测力计和细线的重力及一切摩擦不计,物重G=1
N,则弹簧测力计A和B的示数分别为( )
图4-2-16
A.1
N,0
B.0,1
N
C.2
N,1
N
D.1
N,1
N
【解析】 弹簧测力计的示数等于钩受到的拉力,与弹簧测力计外壳受力无关,物体平衡时绳对物体的拉力F与物重G是一对平衡力,所以F=G=1
N.两弹簧测力计的读数都为1
N,所以D正确.
【答案】 D
7.如图4-2-17所示,弹簧的劲度系数为k,小球重力为G,平衡时球在A位置,今用力F将小球向下拉长x至B位置,则此时弹簧的弹力为( )
图4-2-17
A.kx
B.kx+G
C.G-kx
D.以上都不对
【解析】 对此题,x不是弹簧形变后的长度与不发生形变的长度的差值.球在A位置时弹簧已经伸长了(令它为Δx),这样FB=k(Δx+x)=kΔx+kx.球在A位置平衡时有G=kΔx,所以FB=kx+G,故选项B是正确的.
【答案】 B
8.如图4-2-18所示,物块A静止在斜面B上,下列说法正确的是( )
图4-2-18
A.斜面B对物块A的弹力方向是竖直向上的
B.物块A对斜面B的弹力方向是竖直向下的
C.斜面B对物块A的弹力方向是垂直斜面向上的
D.物块A对斜面B的弹力方向跟物块A恢复形变的方向是相反的
【解析】 斜面B对物块A的弹力方向垂直于斜面向上,A错,C对.物块A对斜面B的弹力方向垂直于斜面向下,跟物块A恢复形变的方向是相同的,B、D错.
【答案】 C
9.一根轻质弹簧一端固定,用大小为F1的力压弹簧的另一端,平衡时长度为l1;改用大小为F2的力拉弹簧,平衡时长度为l2.弹簧的拉伸和压缩均在弹性限度内,该弹簧的劲度系数为( )
A.
B.
C.
D.
【解析】 设弹簧的原长为l,劲度系数为k,由胡克定律F=kx得,F1=k(l-l1),F2=k(l2-l),联立两式求得k=,C正确.
【答案】 C
10.如图4-2-19所示,四个完全相同的弹簧都处于水平位置,它们的右端受到大小皆为F的拉力作用,而左端的情况各不相同:①中弹簧的左端固定在墙上;②中弹簧的左端受大小也为F的拉力作用;③中弹簧的左端拴一小物块,物块在光滑的桌面上滑动;④中弹簧的左端拴一小物块,物块在粗糙的桌面上滑动.若认为弹簧的质量都为零,以l1、l2、l3、l4依次表示四个弹簧的伸长量,则有( )
图4-2-19
A.l1>l2
B.l2>l3
C.l3>l4
D.l1=l2=l3=l4
【解析】 本题考查弹簧所受拉力与弹簧伸长量的关系.弹簧的伸长量等于弹簧弹力与弹簧劲度系数的比值,分析四种情况下弹簧所受弹力都等于外力F,又因弹簧完全相同,劲度系数相同,所以四种情况下弹簧的伸长量相等.
【答案】 D
11.某人设计了一只弹簧测力计,如图4-2-20所示,当弹簧的自由端B未悬挂重物时指针正对刻度5,在弹性限度内,当挂上80
N重物时指针正对刻度45;当指针正对刻度20时,请你探究分析所挂重物的重量为多少?
图4-2-20
【解析】 弹簧的伸长量可用刻度的变化量表示.当所挂重物G1=80
N时,伸长量x1=40;当指针正对刻度20时,弹簧伸长量x2=15.设所挂重物为G2,根据二力平衡和胡克定律得,G1=kx1,G2=kx2,所以G2=G1=×80
N=30
N.
【答案】 30
N
12.
“蹦极”是一种非常刺激的户外休闲运动,人从水面上方某处的平台上跳下,靠自身所受的重力让其自由下落,被拉伸的橡皮绳又会产生向上的力,把人拉上去,然后人再下落.正是在这上上下下的运动中,蹦极者体会到惊心动魄的刺激,如图4-2-21所示.设一次蹦极中所用的橡皮绳原长为15
m.质量为50
kg的人在下落到最低点时所受的向上的最大拉力为3
000
N,已知此人停在空中时,蹦极的橡皮绳长度为17.5
m,橡皮绳的弹力与伸长的关系符合胡克定律.(取g=10
N/kg).求:
图4-2-21
(1)橡皮绳的劲度系数;
(2)橡皮绳的上端悬点离下方的水面至少为多高?
【解析】 (1)人静止于空中时,橡皮绳的拉力F1=500
N.
而F1=k(l-l0),所以橡皮绳劲度系数k==
N/m=200
N/m.
(2)设橡皮绳拉力最大时,绳长为l′.
据胡克定律F2=k(l′-l0)得
l′=+l0=
m+15
m=30
m.
【答案】 (1)200
N/m (2)30
m
同课章节目录
- 第1章 绪论
- 物理学与自然规律
- 物理学与社会发展
- 怎样学习物理学
- 高中物理教材特点
- 第2章 运动的描述
- 导入 认识运动
- 第1节 运动、空间和时间
- 第2节 质点和位移
- 第3节 速度和加速度
- 第3章 匀变速直线运动的研究
- 导入 速度的变化
- 第1节 匀变速直线运动的规律
- 第2节 匀变速直线运动的实验探究
- 第3节 匀变速直线运动实例-自由落体运动
- 第4章 相互作用
- 导入 奇特的力现象
- 第1节 重力与重心
- 第2节 形变与弹力
- 第3节 摩擦力
- 第5章 力与平衡
- 导入 感悟平衡之美
- 第1节 力的合成
- 第2节 力的分解
- 第3节 力的平衡
- 第4节 平衡条件的应用
- 第6章 力与运动
- 导入 跨越时空的对话
- 第1节 牛顿第一定律
- 第2节 牛顿第二定律
- 第3节 牛顿第三定律
- 第4节 超重与失重
- 本章复习与测试
