命题名家谈中考命题

课件15张PPT。新课标下的数学中考命题 一份好试卷，应有和谐的结构和适量的亮点，使人看起来应是“出乎意料之外，又在情理之中”.要达到这种层次，我们必须会编好题、编新题.编题是一项有趣味、有价值、有意义，同时也是一项非常艰辛的教研活动.怎样编出含金量高的试题.首先要把握新课程标准，其次要植根于现行教材，在课本中，实际生活中寻找编题的突破口，或改编，或引申或移植，或原创，有时会“移花接木”，有时需新旧结合，有时又需展开想象.总之，编题是有法而又无定法，下面我就自己在命题实践中的感受谈谈自己的作法.一、改编习题 刷新陈题 （1）由“正向思维”变“逆向思维” 所谓改编习题就是利用已有题目，既在呈现的方式上进行变换，又在实质上、思维角度有所改变，使问题变得更加灵活，思维空间更大.原题：在Rt△ABC中，∠C=900，AC=1，BC=3则sinB= ___________.
朝着此题的思维反向进行改编为例1、如图，在正方形网格中，小格的顶点叫格点，请你以三个格点为顶点画一个直角三角形，其中一个内角的正弦值为（2）由“静态”变“动态” 一、改编习题 刷新陈题原题：（2001宁夏）如图，已知在⊙O中，半径OA⊥OB，
C是OB延长线上一点，AC交⊙O于D，求证：弧AD的度数是∠C度数的2倍（用三种方法证明）
通过对此题的观察可发现点C位置不固定，其中蕴含了动态感，因此本题可改造成如下动态题：
例2、如图，CD是⊙O的直径，半径OA⊥CD于O，直线AB绕着A点转动，分别交直线CD于B，⊙O于P.
（1）在图（1）中直线AB经过点C（B、P与C重合）时，∠ABD的度数与弧AP的度数关系是_______________；
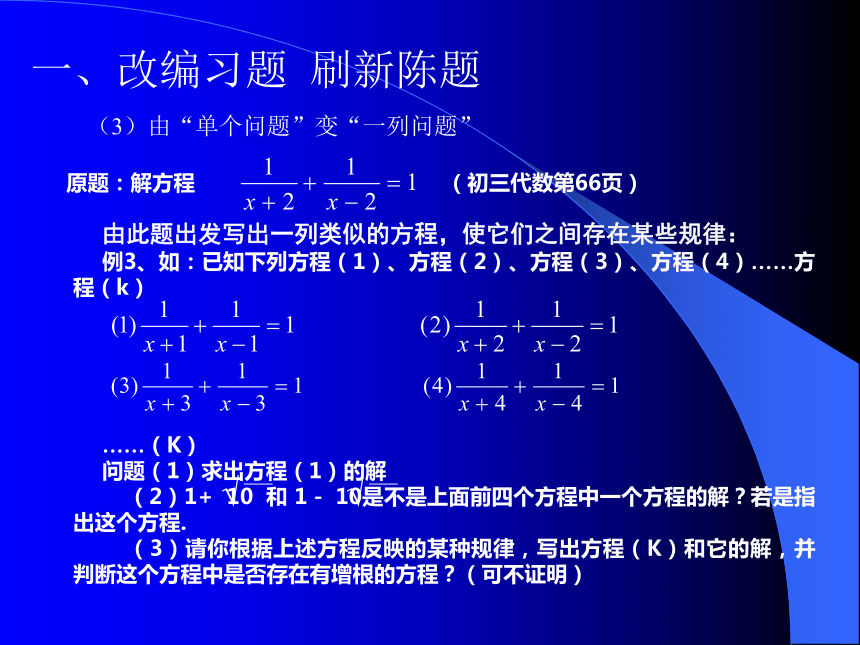
（2）当直线AB分别不经过C、O、D三点时，在图（2）、图（3）的两种情况下，∠ABD的度数与弧AP的度数的关系是否都与第（1）问相同，并在图（2）、图（3）中选一个证明你对该情况下的结论.AAACCCOOODDDP. BBPPB（1）（2）（3）（3）由“单个问题”变“一列问题” 一、改编习题 刷新陈题原题：解方程（初三代数第66页）由此题出发写出一列类似的方程，使它们之间存在某些规律：
例3、如：已知下列方程（1）、方程（2）、方程（3）、方程（4）……方程（k）
……（K）
问题（1）求出方程（1）的解
（2）1+ 10 和 1－ 10是不是上面前四个方程中一个方程的解？若是指出这个方程.
（3）请你根据上述方程反映的某种规律，写出方程（K）和它的解，并判断这个方程中是否存在有增根的方程？（可不证明）
原题：(2004年 南昌)欣赏下面各等式
32+42=52102+112+122=132+142
请写出下一个由7个连续正整数组成，前4个数的平方和等于后3个数的平方和的等式为_________
将此题拓展，引申如下：
例4、观察下列等式，解答下列问题
等式（1）：32+42=52
等式（2）：102+112+122=132+142
等式（3）212+222+232+242=252+262+292
……
等式（n）
（1）由上述等式可知，每个等式中紧靠等于左边的数分别是42、122、242……，这些数存在规律(4×1)2，[4×(1+2)]2,[4×(1+2+3)]2……请你根据这个规律直接写出等式（4）；
（2）若紧靠左边的数是2202，那么该等式是多少个连续正整数平方和组成的？ 一、改编习题 刷新陈题（4）由“小题”变“大题” 数学来源于生活，生活中处处有数学，所以关注生活中的数学是编制数学题的“活水源头”.只要你从不同角度，用搜寻的眼光审视每一个与数学有关联的问题，创新灵感必然会降临.二、更新理念，原创试题 所谓原创题（也可称创新题）就是试题的背景、知识结构、思维角度、问题的呈现方式，都与现有试题不雷同，并突出试题独特的立意，体现新课程理念和思维的创新.
如何编制原创题呢？（1）从实际生活中提炼｛｝例5 1、某单位用钢筋焊接的护栏中有如下图所示规律的图案（图案中四边形均为正方形）：
（1）第3个图案大小正方形共有_________个
（2）第n个图案大小正方形共有__________个
二、更新理念，原创试题（1）从实际生活中提炼2、某文具商店有一次进了一批每只进价为5元的文具盒，开始的标价在进价的基础上增加的百分数为 ，结果标价过高，发现销售不畅，立刻又把标价降低，降低率为（1）设每只文具盒的利润为y，求y与x的函数关系；
（2）要想利润率为20%，开始的标价应是多少？
答①
②10元成15元
，二、更新理念，原创试题（1）从实际生活中提炼最终按第二次标价的8折出售.（2）从操作中发现例6、（2004年，江西）如图，在矩形ABCD中， 近几年来全国各地出现了许多置于剪、拼、折或用学具不同图形中移动，翻转等操作情景中的试题二、更新理念，原创试题AB=3，AD=2，点E F分别在AB、DC 上，AE=DF=2.现把一块直径为2的量角器（圆心为O）放置在图形上，使其0°线MN与EF重合；若将量角器0°线上的端点N固定在点F上，再把量角器绕点F顺时针方向旋转∠α（0°＜α＜90°＝，此时量角器的半圆弧与EF相交与点P，设点P处量角器的读数为n°.（1）用含n°的代数式表示∠α的大小；（2）当n°等于多少时，线段PC与M＇F平行？ （3）在量角器的旋转过程中，过点M＇作GH⊥M＇F，交AE与点G，交AD于点H.设GE=x，ΔAGH的面积为S，试求出S关于x的函数关系式，并写出自变量x的取值范围.证明（略） 例7、如图，已知△ABC、△DCE、△FEG
是三个全等的等腰三角形，底边BC、CE、EG
在同一直线上，且AB= ，BC=1.连结BF，
分别交AC、DC、DE于点P、Q、R.
（1）求证：△BFG～△FEG，并求出BF的长；
（2）观察图形，请你提出一个与点P相关的问题，
并进行解答（根据提出问题的层次和解答过程评分）.
原创题的编拟离不开灵感，而灵感决不会让从来没有经过编题实践的人而突然得到.只有经历艰苦、长期的思考磨练，才会有这种稍纵即逝的思维火花.
（3）从一个图形或一个数学结论去联想二、更新理念，原创试题 有了好的构思不一定能编好题，从素材到成题还需经过精心的雕琢才可能成型.像上面所举例题，哪一道背后不是饱尝命题者的艰辛，几经修改，反复推敲，才形成的.因此，编题时对素材的加工整理不可一蹴而就.三、精心雕琢 提升品位 表述一道试题需要严谨治学的态度，首先，不能出现漏洞，产生歧义，杜绝科学性的错误；再则表述语言力求简洁、准确到位，文字量不宜过长，当然必要的思考铺垫还需进入试题（如例1题中网格及与网格有关表述是一种铺垫的内容），它能方便学生答题，同时，又能反映学生的思维过程，增加试题的效度.（1）简洁准确地表达试题情境三、精心雕琢 提升品位 既要按照思维规律，由浅入深、由简单到复杂，前为后做铺垫，后为前做深化，引导考生逐步解决目标问题来设置问题，又要注意思维的发散，在适当的地方设置开放性、探索性等有价值的设问，这样有利于增强试题考查功能.
总之，试题的改造或创新都需要信心、耐心、灵感及严谨的科学态度，有了这些我们一定能够编出和谐、优美的试题. （2）要科学地设置问题三、精心雕琢 提升品位谢谢大家！