5.1 力的合成 课件 (2)

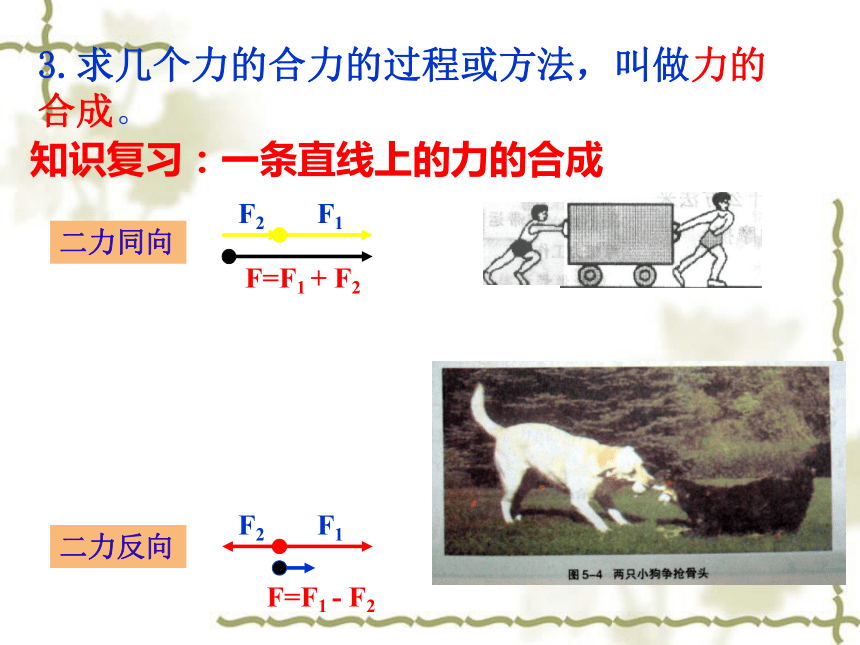
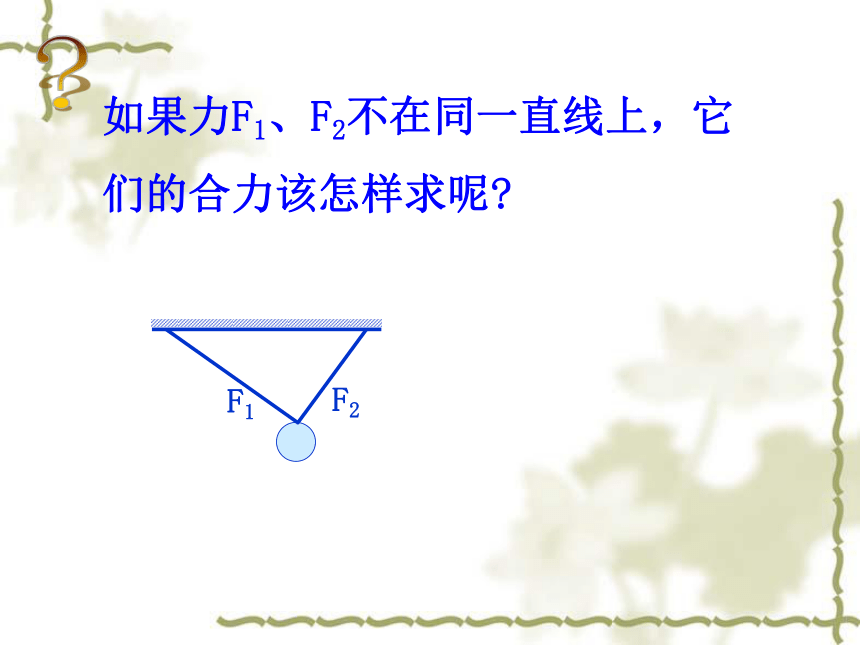
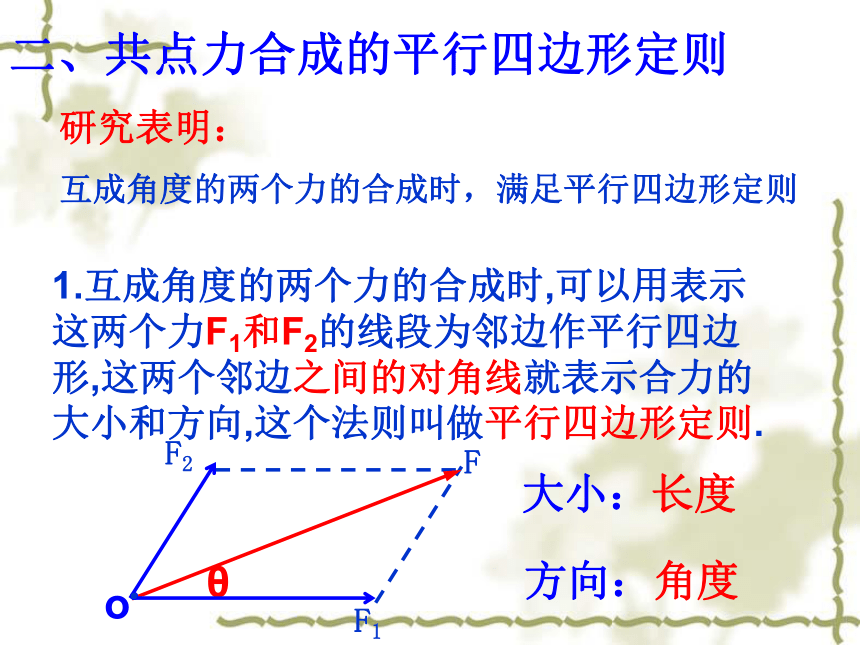
课件25张PPT。第一节 力的合成高一物理第五章一、共点力的合成1．共点力：几个力如果都作用在物体的同一点，或它们的作用线相交于同一点，这几个力叫共点力．2.一个力产生的效果如果能跟原来几个力共同作用在物体上时产生的效果相同，这个力就叫做那几个力的合力，原来的几个力叫做这个力的分力。 合力与分力的关系是“等效替代”。知识复习：一条直线上的力的合成F2F1F=F1 + F2F=F1 - F2二力同向二力反向3.求几个力的合力的过程或方法，叫做力的合成。 ?如果力F1、F2不在同一直线上，它们的合力该怎样求呢?二、共点力合成的平行四边形定则1.互成角度的两个力的合成时,可以用表示这两个力F1和F2的线段为邻边作平行四边形,这两个邻边之间的对角线就表示合力的大小和方向,这个法则叫做平行四边形定则.互成角度的两个力的合成时，满足平行四边形定则研究表明：F大小：长度方向：角度θ实验器材:
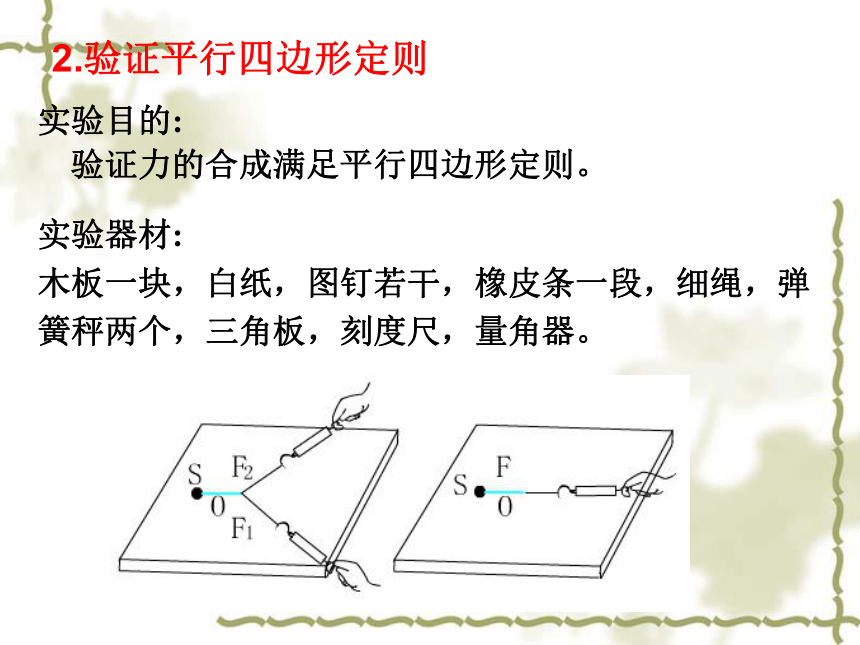
木板一块，白纸，图钉若干，橡皮条一段，细绳，弹簧秤两个，三角板，刻度尺，量角器。 实验目的:
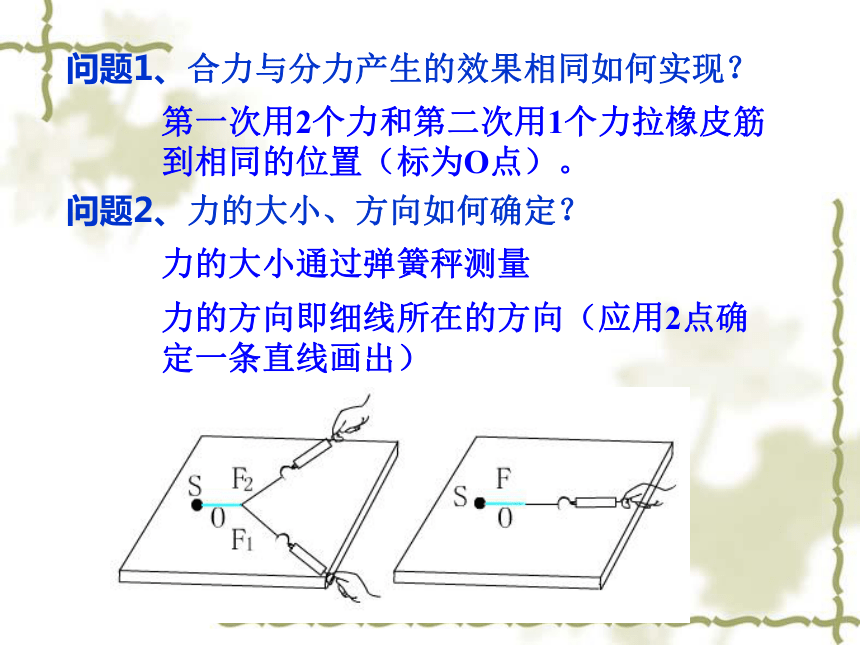
验证力的合成满足平行四边形定则。2.验证平行四边形定则 问题1、合力与分力产生的效果相同如何实现？问题2、力的大小、方向如何确定？第一次用2个力和第二次用1个力拉橡皮筋到相同的位置（标为O点）。力的大小通过弹簧秤测量力的方向即细线所在的方向（应用2点确定一条直线画出）此实验是要用互成角度的两个力与一个力产生相同的效果（即：使橡皮条伸长到同一位置），看其用平行四边形定则求出的合力与这一个力是否在实验误差允许范围内相等，如果在实验误差允许范围内相等，就验证了力的平行四边形定则。实验原理:实验步骤:1．用图钉把一张白纸钉在水平桌面上的方木板上。2．用图钉把橡皮条的一端固定在板上的A点，用两条细绳套结在橡皮条的另一端。3．用两个弹簧秤分别钩住两个细绳套，互成角度地拉橡皮条，使橡皮条伸长，结点到达某一位置O（如图所示）。4．用铅笔描下结点O的位置和两
条细绳套的方向，并记录弹簧秤
的读数。在白纸上按比例作出两
个弹簧秤的拉力F1和F2的图示，
利用刻度尺和三角板根椐平行四
边形定则求出合力F。5．只用一个弹簧秤，通过细绳套把橡皮条的结点拉到与前面相同的位置O,记下弹簧秤的读数和细绳的方向.按同样的比例用刻度尺从O点起做出这个弹簧秤的拉力F'的图示。6．比较F'与用平行四边形定则求得的合力F，在实验误差允许的范围内是否相等。7．改变两个分力F1和F2的大小和夹角。再重复实验两次,比较每次的F与F '是否在实验误差允许的范围内相等。实验现象：表示合力F'的有向线段与平行四边形的对角线F在实验误差允许的范围内重合。实验结论：两个互成一定角度的共点力的合力，可以用这两个力的有向线段为邻边所画的平行四边形的对角线来表示。对角线的长度表示合力的大小，对角线的方向就是合力的方向例：某同学做“验证力的平行四边形定则”实验时，主要步骤是：
A. 在桌上放一块方木板，在方木板上铺一张白纸，用图钉把白纸钉在方木板上
B. 用图钉把橡皮条的一端固定在板上的A点，在橡皮条的另一端拴上两条细绳，细绳的另一端系着绳套
C. 用两个弹簧秤分别钩住绳套，互成角度地拉橡皮条，使橡皮条伸长，结点到达某一位置O．记录下O点的位置，读出两个弹簧秤的示数
D. 按选好的标度,用铅笔和刻度尺作出两只弹簧秤的拉力F1和F2的图示,并用平行四边形定则求出合力F
E. 只用一只弹簧秤，通过细绳套拉橡皮条使其伸长，读出弹簧秤的示数，记下细绳的方向，按同一标度作出这个力F′的图示. F. 比较力F′和F的大小和方向, 看它们是否相同, 得出结论.
上述步骤中：
①有重要遗漏的步骤的序号是 和 ；
②遗漏的内容分别是 和
．CEC中未记下两条绳子的方向E中未说明是否把橡皮条的结点拉到了位置O3.互成角度的两个力合成的方法平行四边形定则 （1）图解法　从力的作用点沿两个分力的作用方向，按同一标度作出两个分力F 1和F 2,并画成一个平行四边形，这个平行四边形的对角线的长度按同样比例表示合力的大小，对角线的方向就是合力的方向。通常可用量角器直接量出它与某一个分力方向的角度。 F大小：长度方向：角度θθ1.如果F1、F2相互垂直，求其合力F合力F的大小：方向：由θ角度确定（计算）（2）计算法　用公式计算出合力的大小。2、两个等大的力的合力若两个分力大小相等时，平行四边形是菱形， 两条对角线互相垂直，合力F的大小为：如果F1和F2的夹角为1200，求合力？合力在角平分线上，大小为：F=F1=F2F ＝ 2×F1 cosα合力F的方向与其中某一个分力F1的夹角α为：F1 和 F2夹角的一半。3．两力夹角为任意时 例. 两个共点力间的夹角是90o，力的大小分别为90 N和120 N，试用作图法和计算法求合力的大小和方向。FO （2）计算法 解：（1）作图法F1F2F3F4F12F123F12344.互成角度的多力合成的方法：逐次合成法思考与讨论：先求两个力的合力，再求出这个合力与第三个力的合力，……，得到合力。如何求多个力的合力？两个共点力F1、F2大小不变，当改变二力间的夹角θ时，其合力F怎样变化？结论：互成角度的二个共点力如果保持大小不变，它们的合力将随夹角的增大而减小。演示5.合力与分力的关系思考与讨论：F1和F2大小一定,夹角θ增大则F减小（θ减小则F增大）合力可(大于等于小于)一个分力F取值范围：|F1－F2|≤ F≤ F1+F2 结论：三个共点力F1、F2、F3，其合力F的取值范围如何？课后思考与讨论：qF三角形定则:平移分力,使分力首尾连接,从第一个分力始端指向最后一个分力末端的有向线段表示合力大小和方向拓展6.三角形定则 小结1、合力与分力的关系是“等效替代”。
2、平行四边形定则：不在一条直线的两个力的合成时，以表示这两个力的线段为邻边做平行四边形，这两个邻边之间的对角线就代表合力的大小和方向。
3、合力与分力的大小关系：
（1）合力大小范围︱F1 - F2︱ ≤ F ≤ F1 + F2
合力不一定比分力大
（2）在两个分力F1、F2大小不变的情况下，两个分力的夹角越大，合力越小。