５.2 力的分解 课件 (3)

课件43张PPT。第2节 力的分解温故知新1．两个大小分别为F1和F2(F2＜F1)的力作用在同一点上，它们合力的大小F满足 (　　)
C．F1－F2≤F≤F1＋F2 D．F12－F22≤F2≤F12＋F22
答案：C
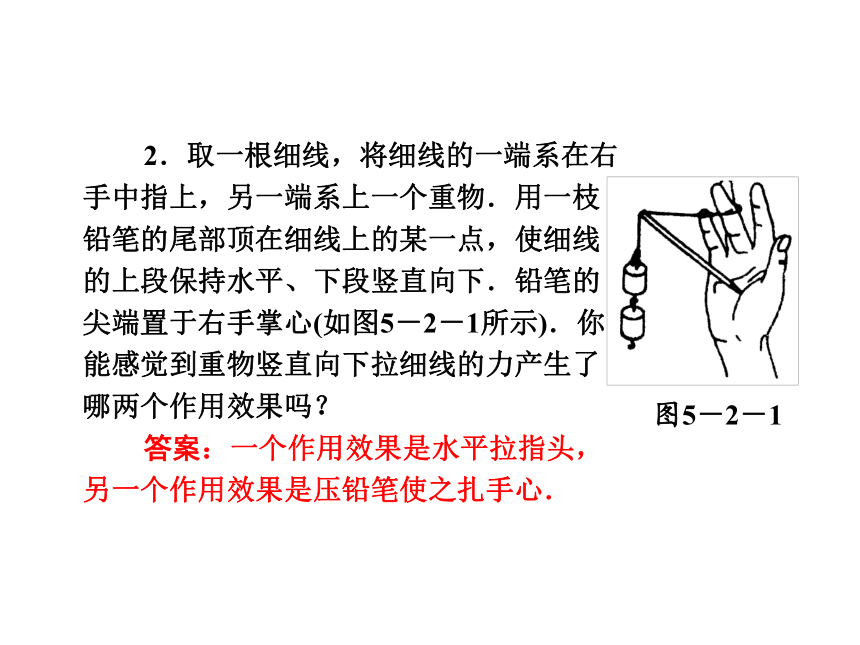
精彩回眸2．取一根细线，将细线的一端系在右手中指上，另一端系上一个重物．用一枝铅笔的尾部顶在细线上的某一点，使细线的上段保持水平、下段竖直向下．铅笔的尖端置于右手掌心(如图5－2－1所示)．你能感觉到重物竖直向下拉细线的力产生了哪两个作用效果吗？
答案：一个作用效果是水平拉指头，另一个作用效果是压铅笔使之扎手心．
图5－2－11．力的分解
(1)定义
求一个力的____叫做力的分解．力的分解是____ ____的逆运算，同样遵守_______________，把一个已知力F作为平行四边形的______，那么，与力F共点的平行四边形的两个____，就表示力F的两个分力．
(2)按力的作用效果分解
先分析力的实际_________确定两个分力的____再根据平行四边形定则求出分力的____．
新知梳理分力力的合成平行四边形定则对角线邻边作用效果大小方向2．力的正交分解
在利用平行四边形定则求合力或分力时，若平行四边形为____，可利用解直角三角形的方法简单计算，有时为了计算简便的需要把一个力沿着两个____的方向分解，这种分解方法叫正交分解．
?
矩形垂直合作探究力的分解
1．对力的分解的理解
(1)遵循法则：力的分解是力的合成的逆运算，同样遵守平行四边形定则．
(2)等效替代：一个力可以用多个分力来等效替代．当分力确定时，合力是唯一的，但合力确定，由于分解方式多种多样，故分力是不唯一的．
2．分解原则及解题思路
(1)分解原则：根据力的实际作用效果分解．
(2)常见实例分析：
(3)解题思路
①先根据力的实际效果确定两个分力的方向；
②再根据两个分力的方向作出力的平行四边形；
③解三角形或解平行四边形，计算出分力的大小和方向，三角形的边长表示力的大小，夹角表示力的方向．
1．如图5－2－2所示，一位重为600 N的演员，悬挂在绳上．若AO绳与水平方向上的夹角为37°，BO绳水平，则 AO、BO两绳受到的力各为多大？若B点位置向上移，AO、BO两绳受到的力各为多大？若B点位置向上移，AO、BO的拉力如何变化？(cos37°＝0.6，cos37°＝0.8)
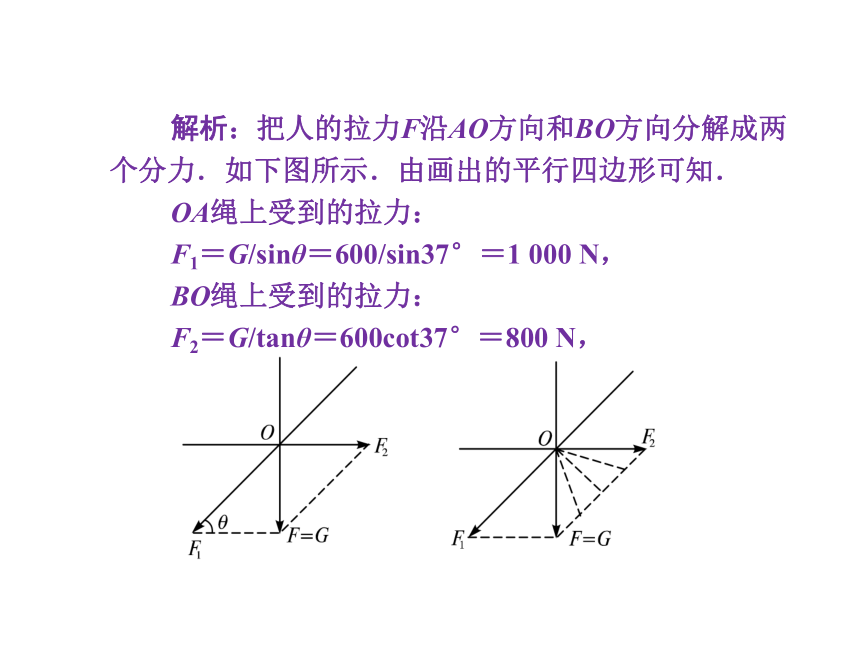
图5－2－2解析：把人的拉力F沿AO方向和BO方向分解成两个分力．如下图所示．由画出的平行四边形可知．
OA绳上受到的拉力：
F1＝G/sinθ＝600/sin37°＝1 000 N，
BO绳上受到的拉力：
F2＝G/tanθ＝600cot37°＝800 N，
若B点上移，人的拉力大小和方向一定不变，利用力的分解方法做出力的平行四边形，可判断出AO绳上的拉力一直在减小、BO绳上的拉力先减小后增大，如上图所示．
答案：见解析
力的正交分解
1．目的：将力的合成化简为同向、反向或垂直方向的分力，便于运用代数运算解决矢量的运算，“分解”的目的是为了更好的“合成”．
2．适用情况：适用于计算三个或三个以上的力的合成．
3．步骤：
(1)建立坐标系：以共点力的作用点为坐标原点，直角坐标系x轴和y轴的选择应使尽量多的力在坐标轴上．
(2)正交分解合力：将每一个不在坐标轴上的力分解到x轴和y轴上，并求出各分力的大小，如图5－2－3所示．
(3)分别求出x轴、y轴上各分力的合力，即：
Fx＝F1x＋F2x＋…，Fy＝F1y＋F2y＋…
图5－2－3特别提醒：(1)求多个力的合力时，一般采用正交分解法．
(2)建立坐标系时，应使尽量多的力落在坐标轴上，以少分解力，求解方便为原则．
2．如图5－2－4所示，重力为500 N的人通过跨过定滑轮的轻绳牵引重200 N的物体，当绳与水平面成60°角时，物体静止．不计滑轮与绳的摩擦．求地面对人的支持力和摩擦力．
图5－2－4解析：人和重物静止，所受合力皆为零，对物体分析得到，绳的拉力F等于物重200 N；人受四个力作用，将绳的拉力分解，即可求解．
如下图所示，以人为研究对象，将绳的拉力分解得
水平拉力
对力的分解时有解无解的讨论
力分解时可能有解或无解，关键看代表合力的对角线与给定的代表分力的有向线段是否能构成平行四边形(或三角形)，若能，即有解；若不能，则无解．具体情况有以下几种：
3．关于力的分解，下列说法正确的是 (　　)
A．力的分解的本质就是用同时作用于物体的几个力产生的作用效果代替一个力的作用效果
B．某个分力的大小可能大于合力大小
C．力的分解是力的合成的逆运算，同样遵循平行四边形定则
D．分解一个力往往根据它产生的效果来分解
答案：ABCD
典例精析 按力的实际效果分解力【典例1】 如图5－2－5所示，光滑斜面的倾角为θ，有两个相同的小球，分别用光滑挡板A、B挡住，挡板A沿竖直方向，挡板B垂直于斜面，则两档板受到小球压力大小之比为多大？斜面受到两小球压力的大小之比为多大？
图5－2－5思路分析：根据两小球所处的位置，正确分析力的作用效果确定分力的方向，作力的平行四边形，力的计算可转化为直角三角形的边角计算，从而求出压力之比．
解析：对球1所受的重力来说，其效果有二：第一，使小球沿水平方向上挤压挡板；第二，使小球垂直压紧斜面．因此，力的分解如图甲所示，由此可得两个分力的大小分别为：F1＝Gtanθ，F2＝G/cosθ
对球2所受的重力G来说，其效果有二：第一，使小球垂直挤压挡板，第二，使小球垂直压紧斜面．因此，力的分解如图乙所示，由此可得两个分力的大小分别为：F3＝Gsinθ，F4＝Gcosθ.
所以挡板A、B所受两个小球压力之比为：F1∶F3＝1∶cosθ，斜面所受两个小球压力之比为：F2∶F4＝1∶cos2θ.
答案：1∶cosθ　1∶cos2θ
反思领悟：按力的作用效果将力进行分解的关键是能够结合实际情况，准确找到力的两个作用效果，依据力的作用效果确定出两个分力的方向．
如图5－2－6所示，质量为m的物体用一轻绳悬挂在水平轻杆BC的端点上，C点由轻绳AC系住．已知AC与BC的夹角为θ，则轻绳AC上的拉力大小为多大？轻杆BC上的压力为多大？
图5－2－6解析：取C点为研究对象，其受力如右图所示．
可将G沿F1和F2的反方向按其作用效果进行分解，由三角形知识得：对力的分解的讨论思路分析：可将平行四边形定则演变、简化为三角形定则，利用三角形知识求解力的合成与分解问题．
解析：如右图所示，由平行四边形定则可知，把分力F2平行移到对边位置，则分力F1、F2与合力F构成一个封闭三角形．
反思领悟：要确定一个力的两个分力，一定要有分解条件．力的分解的求解方法一般是先根据已知条件作出示意图，然后利用平行四边形定则和三角形知识进行定量计算求解．由于力的分解具有多解性，所以在求解时应防止漏解的发生．
把一个力F分解成两分力F1、F2，已知一个分力F1的方向和另一个分力F2的大小，则它的解的情况有几种？试对可能情况进行分析讨论．
解析：本题采用图示法和三角形定则进行分析，从力F的端点O作出分力F1的方向，以F的另一端为圆心，用另一个分力F2的大小为半径作圆．
若F2＜Fsinθ，圆与F1不相交，则无解，如图(a)所示；若F2＝Fsinθ，圆与F1相切，即只有一解，如图(b)所示；若F＞F2＞Fsinθ，圆与F1相割，可得两个三角形，应有两个解，如图(c)所示；若F2＞F，圆与F作用线相交于一点，可得一个三角形，还是一解，如图(d)所示．
答案：三种，讨论见解析
实际生活中力的分解
根据实际情况进行力的分解的具体步骤如下：
(1)先根据力的实际作用效果确定两个分力的方向．
(2)再根据两个分力的方向和待分解力的大小作出力的平行四边形．
(3)然后根据平行四边形或三角形的相关知识求出两个分力的大小和方向．
创新拓展【典例3】 假期里，一位同学在厨房里协助妈妈做菜，对菜刀发生了兴趣．他发现菜刀的刀刃前部和后部的厚薄不一样，刀刃前部的顶角小，后部的顶角大(如图5－2－7所示)，他先后做出过几个猜想，其中合理的是 (　　)图5－2－7所A．刀刃前部和后部厚薄不匀，仅是为了打造方便，外形美观，跟使用功能无关
B．在刀背上加上同样的力时，分开其他物体的力跟刀刃厚薄无关
C．在刀背上加上同样的压力时，顶角越大，分开其他物体的力越大
D．在刀背上加上同样的压力时，顶角越小，分开其他物体的力越大
解析：把刀刃部分抽象后，可简化成一个等腰三角劈，设顶角为2θ，背宽为d，侧面长为l，如图甲所示．
当在刀背施加压力F后，产生垂直侧面的两个分力为F1、F2，使用中依靠这两个分力分开被加工的其他物体．由对称性知，这两个分力大小相等(F1＝F2)，因此画出力分解的平行四边形，实为菱形，如图乙所示．
由此可见，刀背上加上一定的压力F时，侧面分开其他物体的力跟顶角的大小有关，顶角越小，sinθ的值越小，F1和F2越大．但是，刀刃的顶角越小时，刀刃的强度会减小，碰到较硬的物体刀刃会卷口甚至碎裂，实际制造过程中为了适应加工不同物体的需要，所以做成前部较薄，后部较厚．使用时，用前部切一些软的物品(如鱼、肉、蔬菜、水果等)，用后部斩劈坚硬的骨头之类的物品，俗话说：“前切后劈”，指的就是这个意思．故选项D正确．
答案：D