5.4 平衡条件的应用 学案 (5)

5.4
平衡条件的应用
学案5
【学习目标】
1.能用共点力的平衡条件，解决有关力的平衡问题；
2.进一步学习受力分析，正交分解等方法。
3.学会使用共点力平衡条件解决共点力作用下物体平衡的思路和方法，培养灵活分析和解决问题的能力。
【知识梳理】
解共点力平衡问题的一般步骤：
【例题】
例1
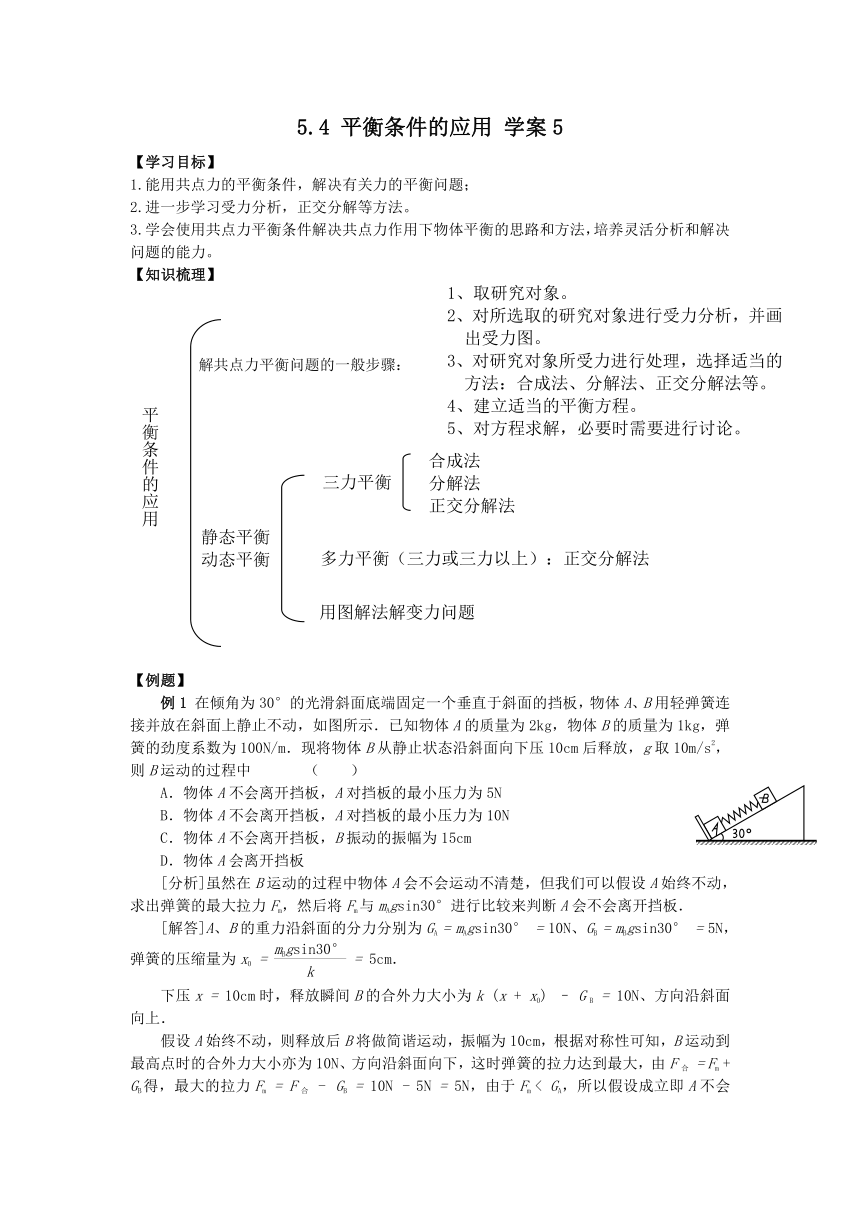
在倾角为30°的光滑斜面底端固定一个垂直于斜面的挡板，物体A、B用轻弹簧连接并放在斜面上静止不动，如图所示．已知物体A的质量为2kg，物体B的质量为1kg，弹簧的劲度系数为100N/m．现将物体B从静止状态沿斜面向下压10cm后释放，g取10m/s2，则B运动的过程中
（
）
A．物体A不会离开挡板，A对挡板的最小压力为5N
B．物体A不会离开挡板，A对挡板的最小压力为10N
C．物体A不会离开挡板，B振动的振幅为15cm
D．物体A会离开挡板
[分析]虽然在B运动的过程中物体A会不会运动不清楚，但我们可以假设A始终不动，求出弹簧的最大拉力Fm，然后将Fm与mAgsin30°进行比较来判断A会不会离开挡板．
[解答]A、B的重力沿斜面的分力分别为GA
=
mAgsin30°
=
10N、GB
=
mBgsin30°
=
5N，弹簧的压缩量为x0
=
=
5cm．
下压x
=
10cm时，释放瞬间B的合外力大小为k
(x
+
x0)
–
G
B
=
10N、方向沿斜面向上．
假设A始终不动，则释放后B将做简谐运动，振幅为10cm，根据对称性可知，B运动到最高点时的合外力大小亦为10N、方向沿斜面向下，这时弹簧的拉力达到最大，由F合
=
Fm
+
GB得，最大的拉力Fm
=
F合
-
GB
=
10N
-
5N
=
5N，由于Fm
<
GA，所以假设成立即A不会离开挡板，A对挡板的最小压力为GA
-
Fm
=
5N．
答案A．
[规律小结]因轻弹簧两端分别与两物体连接，其形变发生改变过程需要一段时间，即弹簧的弹力不发生突变，所以释放瞬间弹簧的弹力仍等于释放前的弹力．
注意：由于受到“水平方向上做简谐运动的弹簧振子的平衡位置处弹力为零”定势思维的影响，本题极易认为B振动的振幅为x
+
x0
=
15cm而错选C。
例2.
如图（1）所示，人重为G1=500N，平台重为G2=300N，人用绳子通过滑轮装置拉住平台，滑轮的重量及摩擦均不计，人与平台均处于静止状态，求人对绳子的拉力及人对平台的压力。
解析：求人对绳子的拉力及人对平台的压力，可以把人隔离出来，但仅仅以人为研究对象不可能求出同一直线上的两个力的大小，同时平台也处于平衡状态，所以须同时结合人和平台的平衡条件才能求出这两个力的大小。
分别以人和平台为研究对象进行受力分析，如图（2）所示，人受到重力G1和平台的支持力FN及绳子的拉力作用，而平台受到重力G2，人对它的压力，左边的绳子拉力，右边的绳子拉力。由作用力与反作用力可知，，。
由平衡条件可知：。
【基础训练】
一、选择题
1.
粗糙的水平面上叠放着A和B两个物体，A和B间的接触面也是粗糙的，如果用水平力F拉B，而B仍保持静止（如图），则此时
（　　）
A.
B和地面间的静摩擦力等于F，B和A间的静摩擦力也等于F
B.
B和地面间的静摩擦力等于F，B和A间的静摩擦力等于零
C.
B和地面间的静摩擦力等于零，B和A间的静摩擦力也等于零
D.
B和地面间的静摩擦力等于零，B和A间的静摩擦力等于F
2.
电风扇悬于天花板上，静止时，扇对天花板拉力为T1，当电风扇工作时，对天花板拉力为T2，则（
）
A.
T1=T2
B.
T1＞T2
C.
T1＜T2
D.
不能确定
3.
如图所示，在一木块上放一铁块m，从水平位置开始缓慢地抬起长板一端，另一端保持位置不变，则此过程中铁块受到摩擦力的大小（
）
A.
随抬起角度α的增大而逐渐减小
B.
随抬起角度α的增大而不断增大
C.
与抬起角度α的大小没有关系
D.
先随抬起角度α的增大而增大，当铁块开始滑动后，又随抬起角度α的增大而减小
4.
三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同，它们共同悬挂一重物，如图所示，其中OB是水平的，A端、B端固定。若逐渐增加C端所挂物体的质量，则最先断的绳（
）
A.
必定是OA
B.
必定是OB
C.
必定是OC
D.
可能是OB，也可能是OC
5.
如图所示，在倾角为30°的斜面上，有一重10N的物块，被平行于斜面的大小为8N的恒力F推着沿斜面匀速上行。在推力F突然取消的瞬间，物块受到的合力大小为（
）
A.
8N
B.
5N
C.
3N
D.
2N
参考答案
一、选择题
1.
B
2.
B
3.
D
4.
A
5.
A
【反思】
收获
疑问
平衡条件的应用
静态平衡
动态平衡
三力平衡
多力平衡（三力或三力以上）：正交分解法
合成法
分解法
正交分解法
用图解法解变力问题
取研究对象。
2、对所选取的研究对象进行受力分析，并画出受力图。
3、对研究对象所受力进行处理，选择适当的方法：合成法、分解法、正交分解法等。
4、建立适当的平衡方程。
5、对方程求解，必要时需要进行讨论。