第6章 力与运动 章末整合课件 (1)

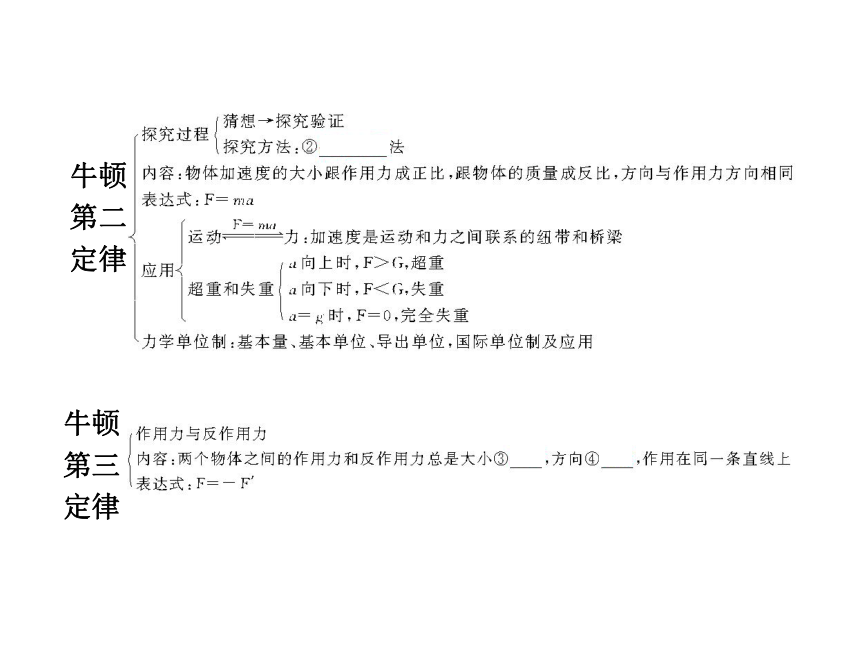
课件43张PPT。章 末 整 合网络建构牛
顿
第
一
定
律伽利略的科学研究方法：“理想实验”加“①_________”科学推理内容：一切物体产，总保持匀速直线运动状态或静
止状态，除非作用在它上面的力迫使它改变
这种状态
惯性：物体具有保持原来匀速直线运动状态或静止
状态的性质牛顿
第二
定律 牛顿
第三
定律 专题讲座牛顿运动定律的理解1.牛顿第一定律
(1)说明了物体不受外力时的运动状态是匀速直线运动或静止．由此可知，力不是维持物体运动的原因．
(2)一切物体都有保持匀速直线运动状态或静止状态的特性——惯性．
①一切物体都具有惯性．
②惯性是物体的固有属性．
③质量是惯性大小的唯一量度．
(3)一切物体受外力时，都会改变原来的运动状态，即外力是使物体改变运动状态的原因．
2．牛顿第二定律
(1)采用控制变量法研究得出了加速度与力和质量的定量关系，即牛顿第二定律．
(2)揭示了a与F、m的定量关系，特别是a与F的几种特殊的对应关系：瞬时性、同向性、正比性、因果性、相对性、同体性．
(3)牛顿第二定律进一步揭示了力与运动的关系，一个物体的运动情况决定于物体受力情况和初始状态．
(4)加速度是联系受力情况和运动情况的桥梁，无论是由受力情况确定运动情况，还是由运动情况确定受力情况，都需求出加速度．
3．牛顿第三定律
“三个一样”是指作用力和反作用力大小一样，力的性质一样，力产生和消失的时刻及变化情况一样．
“两个不一样”是指作用力和反作用力的方向不一样，作用对象即受力物体不一样．另外还需注意区别一个力的反作用力和它的平衡力这两个不同的概念．
【例1】 铅球从运动员手中抛出后做轨迹为抛物线的运动，倘若在空中飞行时，地球的引力突然消失，不计空气阻力，那么铅球此后将 (　　)
?A．立即停止 B．慢慢停下来
C．仍做曲线运动 D．做匀速直线运动
解析：抛在空中的铅球只受重力作用，如果地球引力消失，则铅球不受任何力作用，符合牛顿第一定律的情况．因为铅球在引力突然消失之前是运动的，所以应保持匀速直线运动状态．
答案：D
处理动力学两类基本问题的方法1．两类问题
(1)已知受力情况求运动情况：先由牛顿第二定律求出a，再由运动学公式求运动情况．(如v0、v、s、t等)
(2)已知运动情况求受力情况：先由运动学公式求出a，再由牛顿第二定律求力．
2．解题关键
抓住两个分析：
(1)受力分析；
(2)运动分析，建立物体运动的物理情景．
?
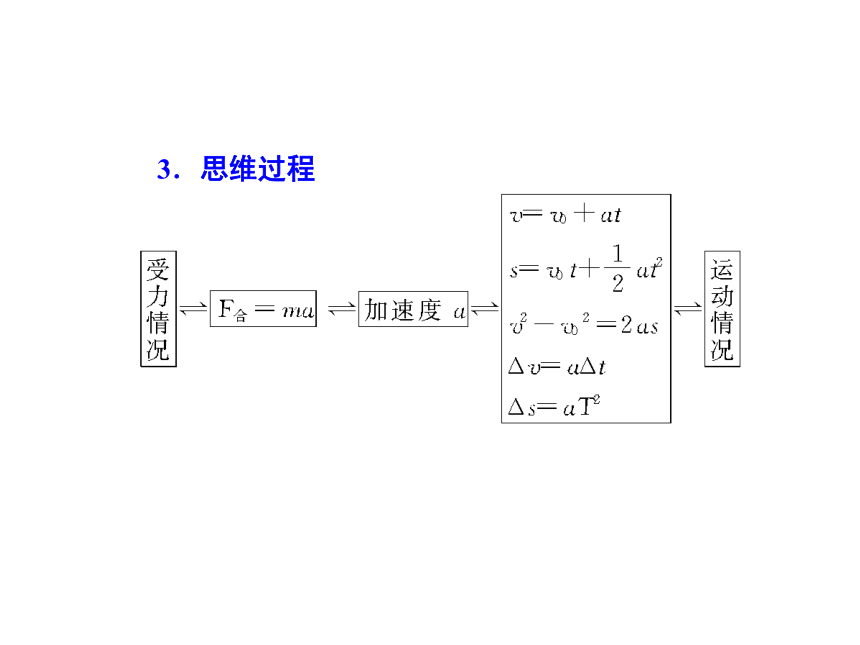
3．思维过程
4．解题步骤
(1)确定研究对象，明确物理过程．
(2)分析研究对象的受力情况和运动情况，必要时画出受力示意图和过程示意图．
(3)根据牛顿第二定律和运动学公式列方程．合力的求解常用合成法或正交分解法，要特别注意公式中各矢量的方向及正负号的选择．
(4)求解、检验，必要时需讨论．
【例2】 如图6－1所示，在倾角θ＝37°的足够长的固定的斜面底端有一质量m＝1 kg的物体，物体与斜面间动摩擦因数μ＝0.25.现用轻细绳将物体由静止沿斜面向上拉动，拉力F＝10 N，方向平行斜面向上，经时间t＝4 s绳子突然断了．求：
图6－1(1)绳断时物体的速度大小．
(2)从绳子断了开始到物体再返回到斜面底端的运动时间．
(sin37°＝0.60，cos37°＝0.80，g＝10 m/s2)
解析：(1)物体受拉力向上运动过程中，受拉力F、斜面的支持力N、重力mg和摩擦力f，如下图所示，设物体向上运动的加速度为a1，根据牛顿第二定律有：
F－mgsinθ－f＝ma1
因f＝μN，N＝mgcosθ
解得a1＝2 m/s2
t＝4 s时物体的速度大小为v1＝a1t＝8 m/s.
(2)绳断时物体距斜面底端的位移
绳断后物体沿斜面向上做匀减速直线运动，设运动的加速度大小为a2，受力如右图所示，则根据牛顿第二定律，对物体沿斜面向上运动的过程有mgsinθ＋f＝ma2
f＝μmgcosθ
解得a2＝8 m/s2
此后物体将沿着斜面匀加速下滑，设物体下滑的加速度为a3，受力如右图所示，根据牛顿第二定律对物体加速下滑的过程有
mgsinθ－f＝ma3
f＝μmgcosθ
解得a3＝4 m/s2
答案：(1)8 m/s　(2)4.2 s
连接体的求解方法牛顿运动定律既可处理单个物体的力和运动的问题，也可处理多个物体组成的系统的力和运动的问题．在处理多个物体组成的系统的力和运动的问题时，往往采用整体法和隔离法．
1．整体法
整体法是将几个物体看作一个整体作为研究对象．
在研究系统的加速度和力的关系时，牛顿第二定律F＝ma中，F是整体所受的合力，而物体之间和物体各部分之间的相互作用的力可以不考虑，这样就简化了受力分析．
2．隔离法
隔离法是将物体从系统中隔离出来作为研究对象，一般在求解系统内各物体相互作用力时使用．
【例3】如图6－2所示，在光滑的水平面上有一个质量mC＝4 kg的小车C，物体A和B通过车上的滑轮用细绳相连．它们的质量分别为mA＝6 kg，mB＝1 kg，A与C之间的图6－2解析：由于A、B、C三者一起向左做匀加速运动，说明三者具有相同的加速度，因此可以把三者看作一个系统，作为一个整体来研究，这个整体的质量等于各物体质量之和，整体在水平方向上所受的外力为F，根据牛顿第二定律即可求出整体的加速度．再隔离A和B分别进行受力分析，即可求出外力F，显然当F最大时，加速度a也最大，此时A刚刚要开始滑动．
设整体运动的最大加速度为a，视A、B、C为一系统，则系统在水平方向上由牛顿第二定律可得
F＝(mA＋mB＋mC)a ①
隔离A和B，分别对A、B进行受力分析，如下图所示．
对于A由牛顿第二定律可得
T－μmAg＝mAa. ②
?
对于B进行正交分解，由牛顿第二定律得
Tcosθ－mBg＝0 ③
F－Tsinθ＝mBa ④
由①④两式可得
Tsinθ＝(mA＋mC)a ⑤
答案：20.7 N　1.88 m/s2
超重和失重问题1．物体超重或失重的本质不是重力增加了或减小了，而是物体对支持面的压力或对悬挂物体的拉力大于或小于物体的实际重力．
2．物体超重还是失重与速度方向和大小无关，我们可以根据加速度的方向判断超重还是失重，如果加速度方向向上或加速度的竖直分量向上，则超重；如果加速度方向向下，或加速度的竖直分量向下，则失重．
3．物体处于完全失重状态时，物体与重力有关的一些现象就会全部消失，比如：①与重力有关的一些仪器如天平、台秤等不能再使用，②竖直上抛的物体再也回不到地面，③杯口向下时，杯中的水也不流出．
【例4】 如图6－3所示，在一升降机中，物体A置于斜面上，当升降机处于静止状态时，物体A恰好静止不动，若升降机以加速度g竖直向下做匀加速直线运动时，以下关于物体受力的说法中正确的是 (　　)
图6－3A．物体仍然相对斜面静止，物体所受的各个力均不变
B．因物体处于失重状态，所以物体不受任何力作用
C．因物体处于完全失重状态，所以物体所受重力变为零，其他力不变
D．物体处于完全失重状态，物体除了受到的重力不变以外，不受其他力的作用
解析：当物体以加速度g向下做匀加速直线运动时，物体处于完全失重状态，其视重为零，因而支持物对其的作用力亦为零；处于完全失重状态的物体，地球对它的引力即重力依然存在．
答案：D
易错分析对牛顿定律的理解不全面【典例1】 在第二十二届世界大学生冬季运动会自由滑比赛中，中国小将张丹/张昊毫无争议地再夺第一名，为中国队夺得第一枚本届大冬会金牌．花样滑冰表演刚开始时他们静止不动，如图6－4所示，随着优美的音乐响起，他们在相互猛推一下后分别向相反方向运动，假定两人的冰刀与冰面间的动摩擦因数相同，已知张丹在冰面上滑行的距离比张昊滑行得远，这是由于 (　　)
图6－4A．在推的过程中，张丹推张昊的力小于张昊推张丹的力
B．在推的过程中，张丹推张昊的时间等于张昊推张丹的时间
C．在刚分开时，张丹的初速度大于张昊的初速度
D．在分开后，张丹的加速度的大小大于张昊的加速度的大小
错因分析：错解1：对牛顿第三定律认识不清，认为两人相互作用的时间关系不能确定，容易漏选B；
错解2：对牛顿第二定律运用不当，不能充分理解“两人的冰刀与冰面间的动摩擦因数相同”的含义，从而不能正确分析两人加速度的大小，错误地根据“张丹在冰面上滑行的距离比张昊滑行得远”而选择D.
解析：张丹和张昊相互推的过程中，两人的推力属作用力和反作用力．根据牛顿第三定律，它们大小相等、方向相反、作用时间相同；由牛顿第二定律可以分析，F＝ma，两人与冰面间的动摩擦因数μ相同，分开后二人的加速度大小相等，都是a＝μg；根据运动学公式0－v02＝－2as容易理解，张丹之所以滑行的距离比张昊滑行得远是因为二人分开时其获得的初速度较大．经过以上分析可见，本题的正确答案是B、C.
答案：BC纠错心得：对牛顿运动定律的认识不够是分析问题出现失误的关键，容易失误的焦点主要是对牛顿第二定律的瞬时性、方向性以及作用力和反作用力的等值性、等时性、相互性的理解．
不会处理瞬时问题【典例2】 如图6－5所示，质量为m的小球与弹簧Ⅰ和水平细绳Ⅱ相连，Ⅰ、Ⅱ的另一端分别固定于P、Q两点．球静止时，Ⅰ中拉力大小 为T1，Ⅱ中拉力大小为T2，当仅剪断Ⅰ、Ⅱ其中一根的瞬间，球的加速度a应是 (　　)
图6－5错因分析：小球受到弹簧Ⅰ的拉力T1、绳Ⅱ的拉力T2和重力mg三力作用保持平衡，若剪断Ⅰ，另外两个力的合力与T1等大反向，故误选C.
答案：AB纠错心得：根据牛顿第二定律知，加速度与合外力存在瞬时对应关系．在分析瞬时对应关系时，应注意两个基本模型特点的区别：(1)轻绳模型：①轻绳不能伸长，②轻绳的拉力可突变；③轻绳各处受力相等，且拉力方向沿着绳子；(2)轻弹簧模型：①轻弹簧各处受力相等，其方向与弹簧形变方向相反，②弹力的大小为F＝kx，其中k是弹簧的劲度系数，x为弹簧的形变量．
找不到临界条件而出错【典例3】 如图6－6所示，一个质量为m＝0.2 kg的小球用细绳吊在倾角为θ＝53°的光滑斜面上，当斜面静止时，绳与斜面平行．当斜面以10 m/s2的加速度向右做加速运动时，求绳子的拉力大小及斜面对小球的弹力大小．
图6－6错因分析：当斜面做加速运动时，小球受到三个力(重力、绳的拉力、支持力)的作用，此时绳仍平行于斜面，根据正交分解法，利用牛顿第二定律列方程：
在水平方向上：Tcosθ－FNsinθ＝ma
在竖直方向上：Tsinθ＋FNcosθ＝mg
将题中各已知量代入方程，无解．找不到正确的方法而无法完成解答．
解析：先分析物理现象．用极限法把加速度a推到两个极端：当a较小(a→0)时，小球受到三个力(重力、拉力、支持力)的作用，此时绳平行于斜面；当a增大(足够大)时，小球将“飞离”斜面，不再受支持力，此时绳与水平方向的夹角未知．那么，当斜面以加速度a＝10 m/s2向右加速运动时，小球是否已离开斜面，为此，必须先求出小球离开斜面的临界值a0.
小球刚要离开斜面时，只受重力和拉力，根据平行四边形定则作出其合力如图所示，由牛顿第二定律得：mgcotθ＝ma0
答案：2.83 N　0纠错心得：解决物理问题要透彻分析物体的运动和受力的情境．而具体情境中存在的各种临界条件往往会掩盖问题的实质，所以有些问题挖掘隐含条件就成为解题的关键．
?