集合的表示,运算
图片预览


文档简介
高一数学集合与集合的表示方法、集合之间的关系、运算人教实(B)
【本讲教育信息】
一. 教学内容:
集合与集合的表示方法、集合之间的关系、运算
二、学习目标
1、首先通过实例,引入集合与集合的元素的概念,接着给出了空集的含义。然后,学习了集合的两种表示方法(列举法和特征性质描述法);从观察集合与集合之间元素的关系开始,给出子集、真子集以及集合相等的概念,同时学习了用维恩(Venn)图表示集合,学习了交集、并集以及全集、补集的初步知识。
2、理解集合的表示法,能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用.
3、理解集合之间包含与相等的含义,能识别给定集合的子集.培养分析、比较、归纳的逻辑思维能力.
4、能在具体情境中,了解全集与空集的含义.理解两个集合的并集与交集的含义,会求两个简单集合的交集与并集.培养从具体到抽象的思维能力.
5、理解在给定集合中,一个子集的补集的含义,会求给定子集的补集.
6、能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用.
三、知识要点
1、集合
①定义:某些指定的对象集在一起就成为一个集合,集合中的每个对象叫做这个集合的元素。
②表示
列举法:将集合中的元素一一列举出来,用大括号括起来,如{a,b,c}
描述法:将集合中的元素的共同属性表示出来,形式为:P={x∣P(x)}.
如:
图示法:用文氏图表示题中不同的集合。
③分类:有限集、无限集、空集。
④性质:确定性:必居其一,
互异性:不写{1,1,2,3}而写{1,2,3},集合中元素互不相同
无序性:{1,2,3}={3,2,1}
2、常用数集
复数集C 实数集R 整数集Z 自然数集N 正整数集(或N+) 有理数集Q
3、元素与集合的关系:
4、集合与集合的关系:
①子集:若对任意都有[或对任意的都有] 则A是B的子集。
记作:
②真子集:若,且存在,则A是B的真子集。
记作:B[或“”] AB,BC AC
③
④空集:不含任何元素的集合,用表示
对任何集合A有,若则A
注:
5、子集的个数
若,则A的子集个数、真子集的个数、非空真子集的个数分别为2n个,2n -1个和2n -2个。
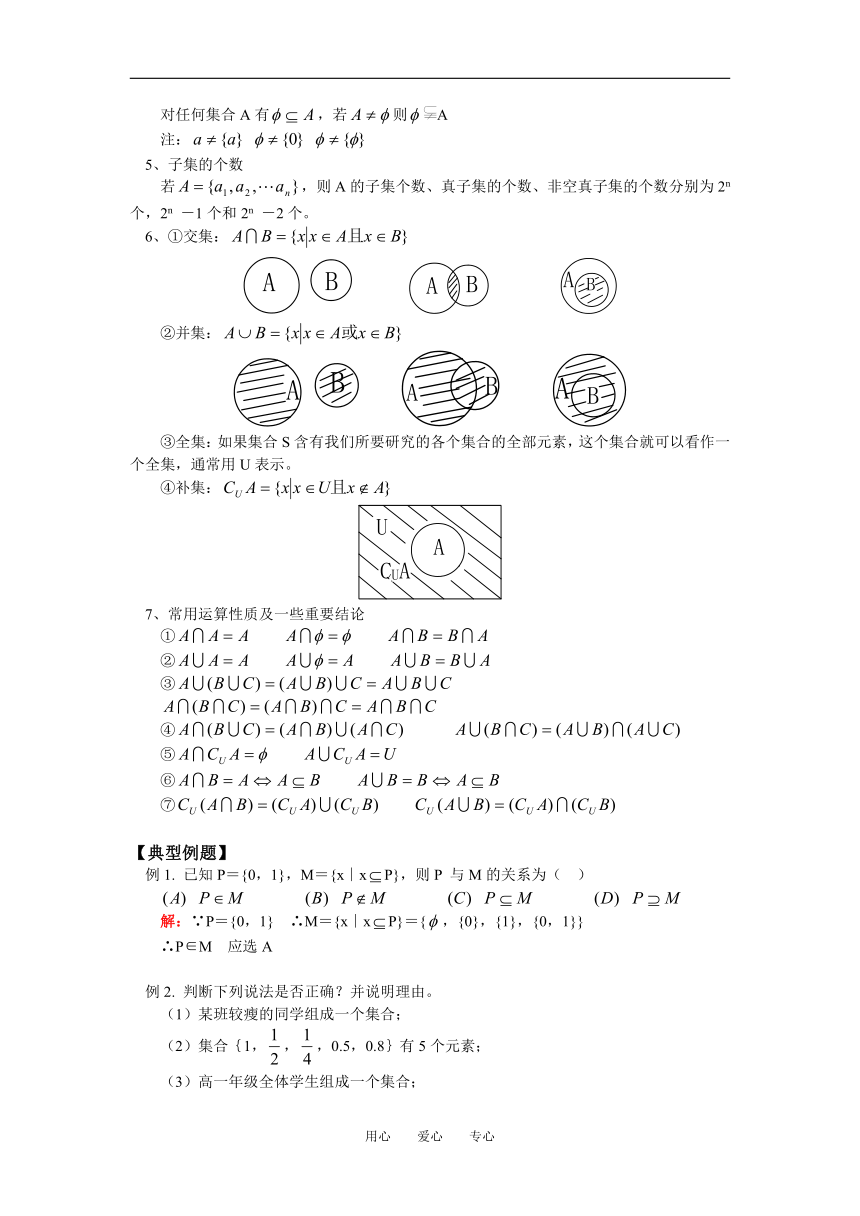
6、①交集:
②并集:
③全集:如果集合S含有我们所要研究的各个集合的全部元素,这个集合就可以看作一个全集,通常用U表示。
④补集:
7、常用运算性质及一些重要结论
①
②
③
④
⑤
⑥
⑦
【典型例题】
例1. 已知P={0,1},M={x∣xP},则P 与M的关系为( )
解:∵P={0,1} ∴M={x∣xP}={,{0},{1},{0,1}}
∴P∈M 应选A
例2. 判断下列说法是否正确?并说明理由。
(1)某班较瘦的同学组成一个集合;
(2)集合{1,,,0.5,0.8}有5个元素;
(3)高一年级全体学生组成一个集合;
(4)集合A={(1,-3)}与B={(-3,1)}是同一集合。
策略:从集合的三个特征入手。
解答:(1)错。因为集合中的每个对象都是确定的。“较瘦的”是一个模糊的不确定的标准。因此(1)是错误的。
(2)错。对于一个给定的集合它的元素必须是互异的,即集合中的任何两个元素都应是不同的,所以这个集合只能有4个元素而不是5个。
(3)对。完全符合集合的特征。
(4)错。A={(1,-3)}表示的是点(1,-3)组成的集合,B={(-3,1)}表示的是点(-3,1)组成的集合。因此集合A、B是不相同的。
总结:1、判断某组对象是否为集合必须同时满足三个特征,缺一不可。
2、注意区分数集与点集的不同。
例3. 已知集合
①若,求实数m的取值范围;
②若,求实数m的取值范围。
解:
①
②
例4. 用列举法表示下列集合:
(1){平方后等于4的数};
(2){绝对值不大于3的整数};
(3){y︱y=x2-2,x≤3,x∈N};
(4){(x,y)︱y=x2-2,x≤3,x∈N}。
思路:列举法就是将集合中的元素不重复、不计次序、不遗漏地列出来。
解:(1)因为平方等于4的数有2和-2,所以平方后等于4的数的集合是{2,-2}
(2)因为绝对值不大于3的整数有-3,3,-2,2,-1,1,0,所以绝对值不大于3的整数组成的集合是{-3,3,-2,2,-1,1,0}。
(3)因为x≤3,x∈N,所以x=0,1,2,3,所以y=-2,-1,2,7。所以{y︱y=x2-2,x≤3,x∈N}用列举法表示为{-2,-1,2,7}。
(4)由上题知,{(x,y)︱y=x2-2,x≤3,x∈N}用列举法表示为{(0,-2),(1,-1),(2,2),(3,7)}。
例5. 已知集合,求实数b的取值范围。
解:,∴两点集M与N无公共点
点集M是一个半圆,点集N是随b变化的一组平行直线
例6. 已知集合A={x︱ax2+2x+1=0,a∈R,x∈R}
(1)若A中只有一个元素,求a的值,并求出这个集合;
(2)若A中至多有一个元素,求a的取值范围。
策略:A表示的是方程ax2+2x+1=0的解集。
解答:(1)当a=0时,方程2x+1=0只有一根x=-;当a≠0时,△=0,即 4-4a=0,所以a=1,这时x1=x2=-1。
所以,当a=0或a=1时,A中只有一个元素分别为-或-1。
(2)A中至多有一个元素包括两种情形,即A中有一个元素和A是空集。当A是空集时,则有a≠0且4-4a<0,解得a>1;结合(1)知:当a=0或a≥1时,A中至多有一个元素。
总结:
1、一般容易忽略a=0的情况;
2、(2)中的a=0或a≥1不能等同于a≥0,因为0到1之间的数不符合条件。
[本讲涉及的主要数学思想方法]
1、数学语言的转换是数学解题的重要方法之一,数学中的符号语言、文字语言及图形语言的互相转换,值得重视。
2、分类讨论的思想在数学的解题中有很重要的应用,一定要做到思考问题要严密,做到不重不漏。
3、数形结合思想在解决相关问题的时候,会起到很好的作用,使一些问题很快就得到解决。
【模拟试题】
一、选择题
1. 不能形成一集合的是 ( )
A. 正三角形的全体 B. 《高一代数》中的所有难题
C. 大于2的所有整数 D. 所有的无理数
2. 用列举法将集合{(x,y)|x∈{1,2},y∈{1,2}}表示为 ( )
A. {1,2}∈A B. {1,2}
C. 2={(2,2)} D. {(1,2),(1,1),(2,1),(2,2)}
*3. 满足{a,b}M{a、b、c、d、e}的集合M的个数有( )个
A. 2 B. 4 C. 7 D. 8
4. 以下四个关系:,,{},,其中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
5. 若集合,,且,则的取值范围为( )
A. B. C. D.
6. 下列四个集合中,是空集的是 ( )
A. B.
C. D.
二、填空题
*7. A={x | x =2n+1,n∈Z},B={x | x=4n+1,n∈Z}则A____B(填,,=)。
8. 已知集合A有10个元素,集合B有8个元素,A∩B有4个元素,则集合
A∪B有________个元素。
9. 已知,,则B= 。
三、解答题
*10. 已知集合A ={a2,a+1,-3},B ={a-3,2a-1,a2+1},且
A∩B={-3},求实数a的值。
11. 已知全集,,。求:,,。
**12. 设,,。
(1),求a的值;
(2),且=,求a的值。
试题答案
一、选择题:
1~6 BDCADD
二、填空题
7、; 8、14; 9、{0,1,2};
三、解答题
10、解: ∵A∩B={-3}
∴-3∈B.
①若a-3=-3,则a=0,则A={0,1,-3},B={-3,-1,1}
∴A∩B={-3,1}与A∩B={-3}矛盾,所以a-3≠-3.
②若2a-1=-3,则a=-1,则A={1,0,-3},B={-4,-3,2}
此时A∩B={-3}符合题意,所以a=-1.
11、解:;
;
;
=={2}。
12、解:
(1)此时当且仅当,由韦达定理可得和同时成立,即;
(2)由于,,故只可能3。
此时,也即或,由(1)可得
PAGE
用心 爱心 专心
【本讲教育信息】
一. 教学内容:
集合与集合的表示方法、集合之间的关系、运算
二、学习目标
1、首先通过实例,引入集合与集合的元素的概念,接着给出了空集的含义。然后,学习了集合的两种表示方法(列举法和特征性质描述法);从观察集合与集合之间元素的关系开始,给出子集、真子集以及集合相等的概念,同时学习了用维恩(Venn)图表示集合,学习了交集、并集以及全集、补集的初步知识。
2、理解集合的表示法,能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用.
3、理解集合之间包含与相等的含义,能识别给定集合的子集.培养分析、比较、归纳的逻辑思维能力.
4、能在具体情境中,了解全集与空集的含义.理解两个集合的并集与交集的含义,会求两个简单集合的交集与并集.培养从具体到抽象的思维能力.
5、理解在给定集合中,一个子集的补集的含义,会求给定子集的补集.
6、能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用.
三、知识要点
1、集合
①定义:某些指定的对象集在一起就成为一个集合,集合中的每个对象叫做这个集合的元素。
②表示
列举法:将集合中的元素一一列举出来,用大括号括起来,如{a,b,c}
描述法:将集合中的元素的共同属性表示出来,形式为:P={x∣P(x)}.
如:
图示法:用文氏图表示题中不同的集合。
③分类:有限集、无限集、空集。
④性质:确定性:必居其一,
互异性:不写{1,1,2,3}而写{1,2,3},集合中元素互不相同
无序性:{1,2,3}={3,2,1}
2、常用数集
复数集C 实数集R 整数集Z 自然数集N 正整数集(或N+) 有理数集Q
3、元素与集合的关系:
4、集合与集合的关系:
①子集:若对任意都有[或对任意的都有] 则A是B的子集。
记作:
②真子集:若,且存在,则A是B的真子集。
记作:B[或“”] AB,BC AC
③
④空集:不含任何元素的集合,用表示
对任何集合A有,若则A
注:
5、子集的个数
若,则A的子集个数、真子集的个数、非空真子集的个数分别为2n个,2n -1个和2n -2个。
6、①交集:
②并集:
③全集:如果集合S含有我们所要研究的各个集合的全部元素,这个集合就可以看作一个全集,通常用U表示。
④补集:
7、常用运算性质及一些重要结论
①
②
③
④
⑤
⑥
⑦
【典型例题】
例1. 已知P={0,1},M={x∣xP},则P 与M的关系为( )
解:∵P={0,1} ∴M={x∣xP}={,{0},{1},{0,1}}
∴P∈M 应选A
例2. 判断下列说法是否正确?并说明理由。
(1)某班较瘦的同学组成一个集合;
(2)集合{1,,,0.5,0.8}有5个元素;
(3)高一年级全体学生组成一个集合;
(4)集合A={(1,-3)}与B={(-3,1)}是同一集合。
策略:从集合的三个特征入手。
解答:(1)错。因为集合中的每个对象都是确定的。“较瘦的”是一个模糊的不确定的标准。因此(1)是错误的。
(2)错。对于一个给定的集合它的元素必须是互异的,即集合中的任何两个元素都应是不同的,所以这个集合只能有4个元素而不是5个。
(3)对。完全符合集合的特征。
(4)错。A={(1,-3)}表示的是点(1,-3)组成的集合,B={(-3,1)}表示的是点(-3,1)组成的集合。因此集合A、B是不相同的。
总结:1、判断某组对象是否为集合必须同时满足三个特征,缺一不可。
2、注意区分数集与点集的不同。
例3. 已知集合
①若,求实数m的取值范围;
②若,求实数m的取值范围。
解:
①
②
例4. 用列举法表示下列集合:
(1){平方后等于4的数};
(2){绝对值不大于3的整数};
(3){y︱y=x2-2,x≤3,x∈N};
(4){(x,y)︱y=x2-2,x≤3,x∈N}。
思路:列举法就是将集合中的元素不重复、不计次序、不遗漏地列出来。
解:(1)因为平方等于4的数有2和-2,所以平方后等于4的数的集合是{2,-2}
(2)因为绝对值不大于3的整数有-3,3,-2,2,-1,1,0,所以绝对值不大于3的整数组成的集合是{-3,3,-2,2,-1,1,0}。
(3)因为x≤3,x∈N,所以x=0,1,2,3,所以y=-2,-1,2,7。所以{y︱y=x2-2,x≤3,x∈N}用列举法表示为{-2,-1,2,7}。
(4)由上题知,{(x,y)︱y=x2-2,x≤3,x∈N}用列举法表示为{(0,-2),(1,-1),(2,2),(3,7)}。
例5. 已知集合,求实数b的取值范围。
解:,∴两点集M与N无公共点
点集M是一个半圆,点集N是随b变化的一组平行直线
例6. 已知集合A={x︱ax2+2x+1=0,a∈R,x∈R}
(1)若A中只有一个元素,求a的值,并求出这个集合;
(2)若A中至多有一个元素,求a的取值范围。
策略:A表示的是方程ax2+2x+1=0的解集。
解答:(1)当a=0时,方程2x+1=0只有一根x=-;当a≠0时,△=0,即 4-4a=0,所以a=1,这时x1=x2=-1。
所以,当a=0或a=1时,A中只有一个元素分别为-或-1。
(2)A中至多有一个元素包括两种情形,即A中有一个元素和A是空集。当A是空集时,则有a≠0且4-4a<0,解得a>1;结合(1)知:当a=0或a≥1时,A中至多有一个元素。
总结:
1、一般容易忽略a=0的情况;
2、(2)中的a=0或a≥1不能等同于a≥0,因为0到1之间的数不符合条件。
[本讲涉及的主要数学思想方法]
1、数学语言的转换是数学解题的重要方法之一,数学中的符号语言、文字语言及图形语言的互相转换,值得重视。
2、分类讨论的思想在数学的解题中有很重要的应用,一定要做到思考问题要严密,做到不重不漏。
3、数形结合思想在解决相关问题的时候,会起到很好的作用,使一些问题很快就得到解决。
【模拟试题】
一、选择题
1. 不能形成一集合的是 ( )
A. 正三角形的全体 B. 《高一代数》中的所有难题
C. 大于2的所有整数 D. 所有的无理数
2. 用列举法将集合{(x,y)|x∈{1,2},y∈{1,2}}表示为 ( )
A. {1,2}∈A B. {1,2}
C. 2={(2,2)} D. {(1,2),(1,1),(2,1),(2,2)}
*3. 满足{a,b}M{a、b、c、d、e}的集合M的个数有( )个
A. 2 B. 4 C. 7 D. 8
4. 以下四个关系:,,{},,其中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
5. 若集合,,且,则的取值范围为( )
A. B. C. D.
6. 下列四个集合中,是空集的是 ( )
A. B.
C. D.
二、填空题
*7. A={x | x =2n+1,n∈Z},B={x | x=4n+1,n∈Z}则A____B(填,,=)。
8. 已知集合A有10个元素,集合B有8个元素,A∩B有4个元素,则集合
A∪B有________个元素。
9. 已知,,则B= 。
三、解答题
*10. 已知集合A ={a2,a+1,-3},B ={a-3,2a-1,a2+1},且
A∩B={-3},求实数a的值。
11. 已知全集,,。求:,,。
**12. 设,,。
(1),求a的值;
(2),且=,求a的值。
试题答案
一、选择题:
1~6 BDCADD
二、填空题
7、; 8、14; 9、{0,1,2};
三、解答题
10、解: ∵A∩B={-3}
∴-3∈B.
①若a-3=-3,则a=0,则A={0,1,-3},B={-3,-1,1}
∴A∩B={-3,1}与A∩B={-3}矛盾,所以a-3≠-3.
②若2a-1=-3,则a=-1,则A={1,0,-3},B={-4,-3,2}
此时A∩B={-3}符合题意,所以a=-1.
11、解:;
;
;
=={2}。
12、解:
(1)此时当且仅当,由韦达定理可得和同时成立,即;
(2)由于,,故只可能3。
此时,也即或,由(1)可得
PAGE
用心 爱心 专心
