1.2 感应电动势与电磁感应定律 学案 (1)
文档属性
| 名称 | 1.2 感应电动势与电磁感应定律 学案 (1) |  | |
| 格式 | zip | ||
| 文件大小 | 48.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-08-15 07:05:05 | ||
图片预览


文档简介
1.2《感应电动势与电磁感应定律》学案
【学习目标】
(1)知道感应电动势及决定感应电动势大小的因素。
(2)理解法拉第电磁感应定律内容、数学表达式。
(3)知道E=BLvsinθ推导过程及其应用。
(4)会用解决问题。
【学习重点】法拉第电磁感应定律探究过程。
【学习难点】感应电流与感应电动势的产生条件的区别。
【学习过程】
1、问题1:既然会判定感应电流的方向,那么,怎样确定感应电流的强弱呢?
要知道电动势和电路中的总电阻
2、问题2:如图所示,在螺线管中插入一个条形磁铁,问
①在条形磁铁向下插入螺线管的过程中,电路中是有电流 为什么
有,电路有闭合且磁通量发生变化
②若有感应电流,是谁充当电源
螺线管
③上图中若电路是断开的,有无感应电流电流?有无感应电动势?
无感应电流电流,但仍有感应电动势
3、产生感应电动势的条件是什么?
只要电路中磁通量发生变化
4、比较产生感应电动势的条件和产生感应电流的条件你有什么发现?
前者不必电路闭合,后者电路要闭合
(一)法拉第电磁感应定律
通过实验,我们可以发现,越大,E感越大,即感应电动势的大小完全由磁通量的变化率决定。精确的实验表明:
电路中感应电动势的大小,跟穿过这一电路磁通量的变化率成正比,即E∝。这就是法拉第电磁感应定律。
E=k
在国际单位制中,电动势单位是伏(V),磁通量单位是韦伯(Wb),时间单位是秒(s),可以证明式中比例系数k=1,(同学们可以课下自己证明),则上式可写成E=
设闭合电路是一个N匝线圈,且穿过每匝线圈的磁通量变化率都相同,这时相当于N个单匝线圈串联而成,因此感应电动势变为:ε=N
对定律的理解:
??⑴要区别磁通量Φ、磁通量的变化量ΔΦ、磁通量的变化量率ΔΦ/Δt
??⑵感应电动势的大小与磁通量的变化率成正比
??⑶感应电动势的方向由楞次定律来判断
(二)导线切割磁感线时的感应电动势
如图所示电路,闭合电路一部分导体ab处于匀强磁场中,磁感应强度为B,ab的长度为L,以速度υ匀速切割磁感线,则产生的感应电动势为E
=
BLυ
导线切割磁感线时的感应电动势计算更简捷公式,需要理解
(1)B,L,υ两两
垂直
(2)导线的长度L应为
有效的切割
长度
(3)导线运动方向和磁感线平行时,E=
0
(4)速度υ为平均值(瞬时值),E就为平均感应电动势
问题:当导体的运动方向跟磁感线方向有一个夹角θ,感应电动势可用上面的公式计算吗?
解析:可以把速度v分解为两个分量:垂直于磁感线的分量v1=vsinθ和平行于磁感线的分量v2=vcosθ。后者不切割磁感线,不产生感应电动势。前者切割磁感线,产生的感应电动势为
E=BLv1=BLvsinθ
在国际单位制中,上式中B、L、v的单位分别是特斯拉(T)、米(m)、米每秒(m/s),θ指v与B的夹角。
(三)公式比较
与功率的两个公式比较得出E=ΔΦ/Δt:求平均电动势E=BLV
:
v为瞬时值时求瞬时电动势,v为平均值时求平均电动势
典型例题:
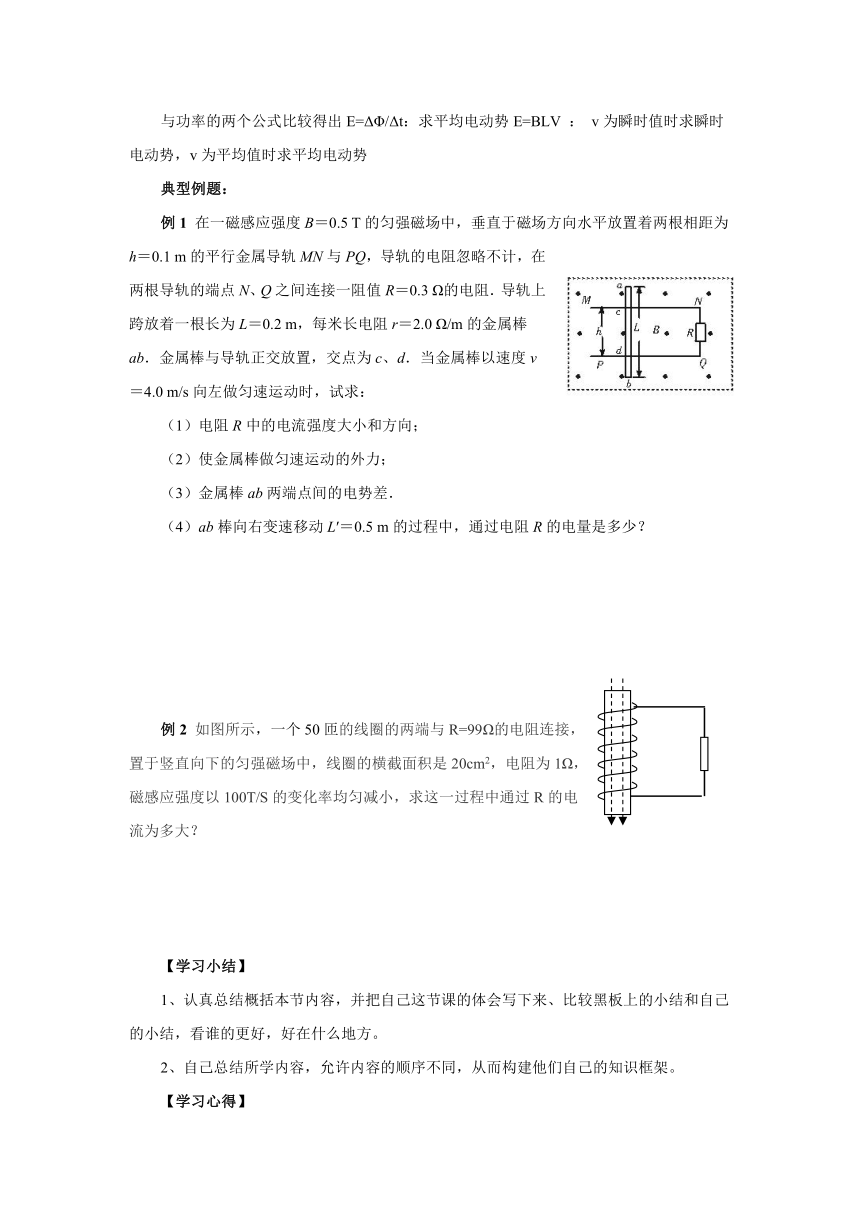
例1
在一磁感应强度B=0.5
T的匀强磁场中,垂直于磁场方向水平放置着两根相距为h=0.1
m的平行金属导轨MN与PQ,导轨的电阻忽略不计,在两根导轨的端点N、Q之间连接一阻值R=0.3
Ω的电阻.导轨上跨放着一根长为L=0.2
m,每米长电阻r=2.0
Ω/m的金属棒ab.金属棒与导轨正交放置,交点为c、d.当金属棒以速度v=4.0
m/s向左做匀速运动时,试求:
(1)电阻R中的电流强度大小和方向;
(2)使金属棒做匀速运动的外力;
(3)金属棒ab两端点间的电势差.
(4)ab棒向右变速移动L′=0.5
m的过程中,通过电阻R的电量是多少?
例2
如图所示,一个50匝的线圈的两端与R=99Ω的电阻连接,置于竖直向下的匀强磁场中,线圈的横截面积是20cm2,电阻为1Ω,磁感应强度以100T/S的变化率均匀减小,求这一过程中通过R的电流为多大?
【学习小结】
1、认真总结概括本节内容,并把自己这节课的体会写下来、比较黑板上的小结和自己的小结,看谁的更好,好在什么地方。
2、自己总结所学内容,允许内容的顺序不同,从而构建他们自己的知识框架。
【学习心得】
__________________________________________________________________________
__________________________________________________________________________
针对性训练:
1.半径为a的圆形区域内有均匀磁场,磁感强度为B
=
0.2T,磁场方向垂直纸面向里,半径为b的金属圆环与磁场同心地放置,磁场与环面垂直,其中a
=
0.4m,b
=
0.6m,金属环上分别接有灯L1、L2,两灯的电阻均为R0
=
2Ω,一金属棒MN与金属环接触良好,棒与环的电阻均忽略不计
(1)若棒以υ0
=
5m/s的速率在环上向右匀速滑动,求棒滑过圆环直径OO′的瞬时(如图所示)MN中的电动势和流过灯L1的电流.
(2)撤去中间的金属棒MN将右面的半圆环OL2O′以OO′为轴向上翻转90 ,若此时磁场随时间均匀变化,其变化率为
eq
\A()=
EQ
\A(
)T/s,求L1的功率.
2
把总电阻为2R的均匀电阻丝焊接成一半径为a的圆周环,水平固定在竖直向下的磁感强度为B的匀强磁场中,如图所示。一长度为2a,电阻等于R,粗细均匀的金属棒MN放在圆环上,它与圆环始终保持良好的电接触。当金属棒以恒定速度V向右移动,经过环心O时,求:(1)棒上电流的大小和方向,及棒两端的电压UMN。
(2)在圆环和金属棒上消耗的总热功率。
3.如图所示,圆环a和b的半径之比R1∶R2=3∶1,且是粗细相同,用同样材料的导线构成,连接两环导线的电阻不计,匀强磁场的磁感应强度始终以恒定的变化率变化,那么,当只有a环置于磁场中与只有b环置于磁场中的两种情况下,AB两点的电势差之比为多少?
4.如图所示,在匀强磁场中,与磁感应强度B成300角放置一边长L=10cm的正方形线圈,共100匝,线圈电阻r=1Ω,与它相连的电路中,电阻R1=4Ω,R2=5Ω,电容C=10μF,磁感应强度变化如图所示,开关s在t0时闭合,在t2=1.5s时又断开。求:
(1)t1=1s时,R2中电流的大小及方向;
(2)s断开后,通过R2的电荷量。
参考答案:
典型例题:
例1
【分析】
金属棒向左匀速运动时,等效电路如图所示.在闭合回路中,金属棒的cd部分相当于电源,内阻rcd=hr,电动势Ecd=Bhv.
【解析】(1)根据欧姆定律,R中的电流强度为
I==0.4
A
方向从N流向Q
(2)使棒匀速运动的外力与安培力是一对平衡力,方向向左,大小为 F=F安=IhB=0.4×0.1×0.5
N=0.02
N
(3)金属棒ab两端的电势差,等于Uac+Ucd+Udb,由于Ucd=IR=Ecd-Ircd,因此也可以写成:
Uab=Eab-Ircd=BLv-Ircd =0.5×0.2×4
V-0.4×0.1×2
V=0.32
V
(4)在ab变速移动L′=0.5
m的过程中通过电阻的电量为
q= =C=5×10-2
C
【评注】
(1)在讨论该类题目时,不要把ab两端的电势差与ab棒产生的感应电动势这两个概念混为一谈.
(2)求电磁感应过程中通过电路的电量时,用到的是平均电流和平均电动势,所以通常用,即q=
所以,通过电路的电量仅由电阻磁通量的改变量决定.
例2
【分析】线圈为等效电源,选择合适公式计算其电动势是关键。
【解析】由法拉第电磁感应定律得线圈中产生的感应电动势为
由闭合电路欧姆定律得感应电流大小为
【评注】在利用全电路欧姆定律时,一定要注意产生感应电动势相当于电源的那部分电路是否具有电阻(内电阻)。
针对性训练:
1.
解析
(1)导体棒MN切割磁感线的有效长度为2a,产生的感应电动势
E1
=
B·
2aυ
=
0.2
×
2
×
0.4
×
5V
=
0.8V
由欧姆定律得流过灯L1的电流I1
=
=
EQ
\A(
)A
=
0.4A
(2)由法拉第电磁感应定律得
eq
\A(
E2
=
)=
EQ
\A(
)πa2
·
eq
\A()=
EQ
\A(
)
×
π
×
0.4
2
×
EQ
\A(
)V
=
0.32V
L1、L2串联,每个灯上分得的电压U
=
0.5E2
=
0.16V
L1的功率为P1
=
=
W
=
1.28×10-2W
2.解:(1)金属棒MN以恒定速度经过圆心O时,产生的感应电动势最大,此时外电路相当于两个相同电阻并联。此时产生的最大电动势为:E=2BaV.
此时感应电流
,其方向由N指向M。则
(2)此时在整个电路中消耗的总热功率为:
3.
3:1
4.0.025A,
向左;1.25×10-6C
【反思】
收获
疑问
L1
L2
b
a
O
O′
N
M
S
A
C
R2
R1
0
1
2
3
t
B
1.5
1.0
0.5
【学习目标】
(1)知道感应电动势及决定感应电动势大小的因素。
(2)理解法拉第电磁感应定律内容、数学表达式。
(3)知道E=BLvsinθ推导过程及其应用。
(4)会用解决问题。
【学习重点】法拉第电磁感应定律探究过程。
【学习难点】感应电流与感应电动势的产生条件的区别。
【学习过程】
1、问题1:既然会判定感应电流的方向,那么,怎样确定感应电流的强弱呢?
要知道电动势和电路中的总电阻
2、问题2:如图所示,在螺线管中插入一个条形磁铁,问
①在条形磁铁向下插入螺线管的过程中,电路中是有电流 为什么
有,电路有闭合且磁通量发生变化
②若有感应电流,是谁充当电源
螺线管
③上图中若电路是断开的,有无感应电流电流?有无感应电动势?
无感应电流电流,但仍有感应电动势
3、产生感应电动势的条件是什么?
只要电路中磁通量发生变化
4、比较产生感应电动势的条件和产生感应电流的条件你有什么发现?
前者不必电路闭合,后者电路要闭合
(一)法拉第电磁感应定律
通过实验,我们可以发现,越大,E感越大,即感应电动势的大小完全由磁通量的变化率决定。精确的实验表明:
电路中感应电动势的大小,跟穿过这一电路磁通量的变化率成正比,即E∝。这就是法拉第电磁感应定律。
E=k
在国际单位制中,电动势单位是伏(V),磁通量单位是韦伯(Wb),时间单位是秒(s),可以证明式中比例系数k=1,(同学们可以课下自己证明),则上式可写成E=
设闭合电路是一个N匝线圈,且穿过每匝线圈的磁通量变化率都相同,这时相当于N个单匝线圈串联而成,因此感应电动势变为:ε=N
对定律的理解:
??⑴要区别磁通量Φ、磁通量的变化量ΔΦ、磁通量的变化量率ΔΦ/Δt
??⑵感应电动势的大小与磁通量的变化率成正比
??⑶感应电动势的方向由楞次定律来判断
(二)导线切割磁感线时的感应电动势
如图所示电路,闭合电路一部分导体ab处于匀强磁场中,磁感应强度为B,ab的长度为L,以速度υ匀速切割磁感线,则产生的感应电动势为E
=
BLυ
导线切割磁感线时的感应电动势计算更简捷公式,需要理解
(1)B,L,υ两两
垂直
(2)导线的长度L应为
有效的切割
长度
(3)导线运动方向和磁感线平行时,E=
0
(4)速度υ为平均值(瞬时值),E就为平均感应电动势
问题:当导体的运动方向跟磁感线方向有一个夹角θ,感应电动势可用上面的公式计算吗?
解析:可以把速度v分解为两个分量:垂直于磁感线的分量v1=vsinθ和平行于磁感线的分量v2=vcosθ。后者不切割磁感线,不产生感应电动势。前者切割磁感线,产生的感应电动势为
E=BLv1=BLvsinθ
在国际单位制中,上式中B、L、v的单位分别是特斯拉(T)、米(m)、米每秒(m/s),θ指v与B的夹角。
(三)公式比较
与功率的两个公式比较得出E=ΔΦ/Δt:求平均电动势E=BLV
:
v为瞬时值时求瞬时电动势,v为平均值时求平均电动势
典型例题:
例1
在一磁感应强度B=0.5
T的匀强磁场中,垂直于磁场方向水平放置着两根相距为h=0.1
m的平行金属导轨MN与PQ,导轨的电阻忽略不计,在两根导轨的端点N、Q之间连接一阻值R=0.3
Ω的电阻.导轨上跨放着一根长为L=0.2
m,每米长电阻r=2.0
Ω/m的金属棒ab.金属棒与导轨正交放置,交点为c、d.当金属棒以速度v=4.0
m/s向左做匀速运动时,试求:
(1)电阻R中的电流强度大小和方向;
(2)使金属棒做匀速运动的外力;
(3)金属棒ab两端点间的电势差.
(4)ab棒向右变速移动L′=0.5
m的过程中,通过电阻R的电量是多少?
例2
如图所示,一个50匝的线圈的两端与R=99Ω的电阻连接,置于竖直向下的匀强磁场中,线圈的横截面积是20cm2,电阻为1Ω,磁感应强度以100T/S的变化率均匀减小,求这一过程中通过R的电流为多大?
【学习小结】
1、认真总结概括本节内容,并把自己这节课的体会写下来、比较黑板上的小结和自己的小结,看谁的更好,好在什么地方。
2、自己总结所学内容,允许内容的顺序不同,从而构建他们自己的知识框架。
【学习心得】
__________________________________________________________________________
__________________________________________________________________________
针对性训练:
1.半径为a的圆形区域内有均匀磁场,磁感强度为B
=
0.2T,磁场方向垂直纸面向里,半径为b的金属圆环与磁场同心地放置,磁场与环面垂直,其中a
=
0.4m,b
=
0.6m,金属环上分别接有灯L1、L2,两灯的电阻均为R0
=
2Ω,一金属棒MN与金属环接触良好,棒与环的电阻均忽略不计
(1)若棒以υ0
=
5m/s的速率在环上向右匀速滑动,求棒滑过圆环直径OO′的瞬时(如图所示)MN中的电动势和流过灯L1的电流.
(2)撤去中间的金属棒MN将右面的半圆环OL2O′以OO′为轴向上翻转90 ,若此时磁场随时间均匀变化,其变化率为
eq
\A()=
EQ
\A(
)T/s,求L1的功率.
2
把总电阻为2R的均匀电阻丝焊接成一半径为a的圆周环,水平固定在竖直向下的磁感强度为B的匀强磁场中,如图所示。一长度为2a,电阻等于R,粗细均匀的金属棒MN放在圆环上,它与圆环始终保持良好的电接触。当金属棒以恒定速度V向右移动,经过环心O时,求:(1)棒上电流的大小和方向,及棒两端的电压UMN。
(2)在圆环和金属棒上消耗的总热功率。
3.如图所示,圆环a和b的半径之比R1∶R2=3∶1,且是粗细相同,用同样材料的导线构成,连接两环导线的电阻不计,匀强磁场的磁感应强度始终以恒定的变化率变化,那么,当只有a环置于磁场中与只有b环置于磁场中的两种情况下,AB两点的电势差之比为多少?
4.如图所示,在匀强磁场中,与磁感应强度B成300角放置一边长L=10cm的正方形线圈,共100匝,线圈电阻r=1Ω,与它相连的电路中,电阻R1=4Ω,R2=5Ω,电容C=10μF,磁感应强度变化如图所示,开关s在t0时闭合,在t2=1.5s时又断开。求:
(1)t1=1s时,R2中电流的大小及方向;
(2)s断开后,通过R2的电荷量。
参考答案:
典型例题:
例1
【分析】
金属棒向左匀速运动时,等效电路如图所示.在闭合回路中,金属棒的cd部分相当于电源,内阻rcd=hr,电动势Ecd=Bhv.
【解析】(1)根据欧姆定律,R中的电流强度为
I==0.4
A
方向从N流向Q
(2)使棒匀速运动的外力与安培力是一对平衡力,方向向左,大小为 F=F安=IhB=0.4×0.1×0.5
N=0.02
N
(3)金属棒ab两端的电势差,等于Uac+Ucd+Udb,由于Ucd=IR=Ecd-Ircd,因此也可以写成:
Uab=Eab-Ircd=BLv-Ircd =0.5×0.2×4
V-0.4×0.1×2
V=0.32
V
(4)在ab变速移动L′=0.5
m的过程中通过电阻的电量为
q= =C=5×10-2
C
【评注】
(1)在讨论该类题目时,不要把ab两端的电势差与ab棒产生的感应电动势这两个概念混为一谈.
(2)求电磁感应过程中通过电路的电量时,用到的是平均电流和平均电动势,所以通常用,即q=
所以,通过电路的电量仅由电阻磁通量的改变量决定.
例2
【分析】线圈为等效电源,选择合适公式计算其电动势是关键。
【解析】由法拉第电磁感应定律得线圈中产生的感应电动势为
由闭合电路欧姆定律得感应电流大小为
【评注】在利用全电路欧姆定律时,一定要注意产生感应电动势相当于电源的那部分电路是否具有电阻(内电阻)。
针对性训练:
1.
解析
(1)导体棒MN切割磁感线的有效长度为2a,产生的感应电动势
E1
=
B·
2aυ
=
0.2
×
2
×
0.4
×
5V
=
0.8V
由欧姆定律得流过灯L1的电流I1
=
=
EQ
\A(
)A
=
0.4A
(2)由法拉第电磁感应定律得
eq
\A(
E2
=
)=
EQ
\A(
)πa2
·
eq
\A()=
EQ
\A(
)
×
π
×
0.4
2
×
EQ
\A(
)V
=
0.32V
L1、L2串联,每个灯上分得的电压U
=
0.5E2
=
0.16V
L1的功率为P1
=
=
W
=
1.28×10-2W
2.解:(1)金属棒MN以恒定速度经过圆心O时,产生的感应电动势最大,此时外电路相当于两个相同电阻并联。此时产生的最大电动势为:E=2BaV.
此时感应电流
,其方向由N指向M。则
(2)此时在整个电路中消耗的总热功率为:
3.
3:1
4.0.025A,
向左;1.25×10-6C
【反思】
收获
疑问
L1
L2
b
a
O
O′
N
M
S
A
C
R2
R1
0
1
2
3
t
B
1.5
1.0
0.5
同课章节目录
- 第1章 电磁感应
- 导入 改变世界的线圈
- 第1节 磁生电的探索
- 第2节 感应电动势与电磁感应定律
- 第3节 电磁感应定律的应用
- 第2章 楞次定律和自感现象
- 导入 奇异的电火花
- 第1节 感应电流的方向
- 第2节 自感
- 第3节 自感现象的应用
- 专题探究 电磁感应的实验与调研
- 第3章 交变电流
- 导入 两种电源
- 第1节 交变电流的特点
- 第2节 交变电流是怎样产生的
- 第3节 交变电流中的电容和电感
- 第4章 远距离输电
- 导入 电如何到我家
- 第1节 三相交变电流
- 第2节变压器
- 第3节 电能的远距离传输
- 专题探究 交变电流的实验与调研
- 第5章 传感器及其应用
- 导入 从芝麻开门说起
- 第1节 揭开传感器的面纱
- 第2节 常见传感器工作原理
- 第3节 大显身手的传感器
- 专题探究 传感器的实验与调研
