人教版高中数学选修2-2(教案)1.7定积分的简单应用(含2课时)
文档属性
| 名称 | 人教版高中数学选修2-2(教案)1.7定积分的简单应用(含2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 189.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-11 15:30:25 | ||
图片预览


文档简介
20
年
月
日
第
课时
课题:
1.7定积分的简单应用(一)
教学目的
1、知识与技能:进一步让学生深刻体会“分割
( http: / / www.21cnjy.com )、以直代曲、求和、逼近”求曲边梯形的思想方法;让学生深刻理解定积分的几何意义以及微积分的基本定理;初步掌握利用定积分求曲边梯形的几种常见题型及方法;体会定积分在物理中应用(变速直线运动的路程、变力沿直线做功)。2、过程与方法:
借助于几何直观定积分的基本思想,了解定积分在实际中的应用3、情感、态度与价值观:
通过定积分在几何和物理中的应用,进一步感受极限的思想
重
点
定积分在几何和物理中的应用
难
点
定积分在几何和物理中的应用
教学过程:
定积分的应用
(一)利用定积分求平面图形的面积
例1.计算由两条抛物线和所围成的图形的面积.
解:,所以两曲线的交点为(0,0)、(1,1),面积S=,所以=
例2.计算由直线,曲线以及x轴所围图形的面积S.
解:作出直线,曲线的草图,所求面积为图阴影部分的面积.
解方程组
得直线与曲线的交点的坐标为(8,4)
.
直线与x轴的交点为(4,0).
因此,所求图形的面积为S=S1+S2
.
例3.求曲线与直线轴所围成的图形面积。
答案:
练习
1、求直线与抛物线所围成的图形面积。
答案:
2、求由抛物线及其在点M(0,-3)和N(3,0)处的两条切线所围成的图形的面积。
略解:,切线方程分别为、
,则所求图形的面积为
3、求曲线与曲线以及轴所围成的图形面积。
略解:所求图形的面积为
4、在曲线上的某点A处作一切线使之与曲线以及轴所围成的面积为.试求:切点A的坐标以及切线方程.
略解:如图由题可设切点坐标为,则切线方程
为,切线与轴的交点坐标为
,则由题可知有
,所以切点坐标与切线方程分别为
总结:
1、定积分的几何意义是:、轴所围成的图形的面积的代数和,即.
2、求曲边梯形面积的方法与步骤:
画图,并将图形分割为若干个曲边梯形;
对每个曲边梯形确定其存在的范围,从而确定积分的上、下限;
确定被积函数;
求出各曲边梯形的面积和,即各积分的绝对值的和。
3、几种常见的曲边梯形面积的计算方法:
(1)型区域:
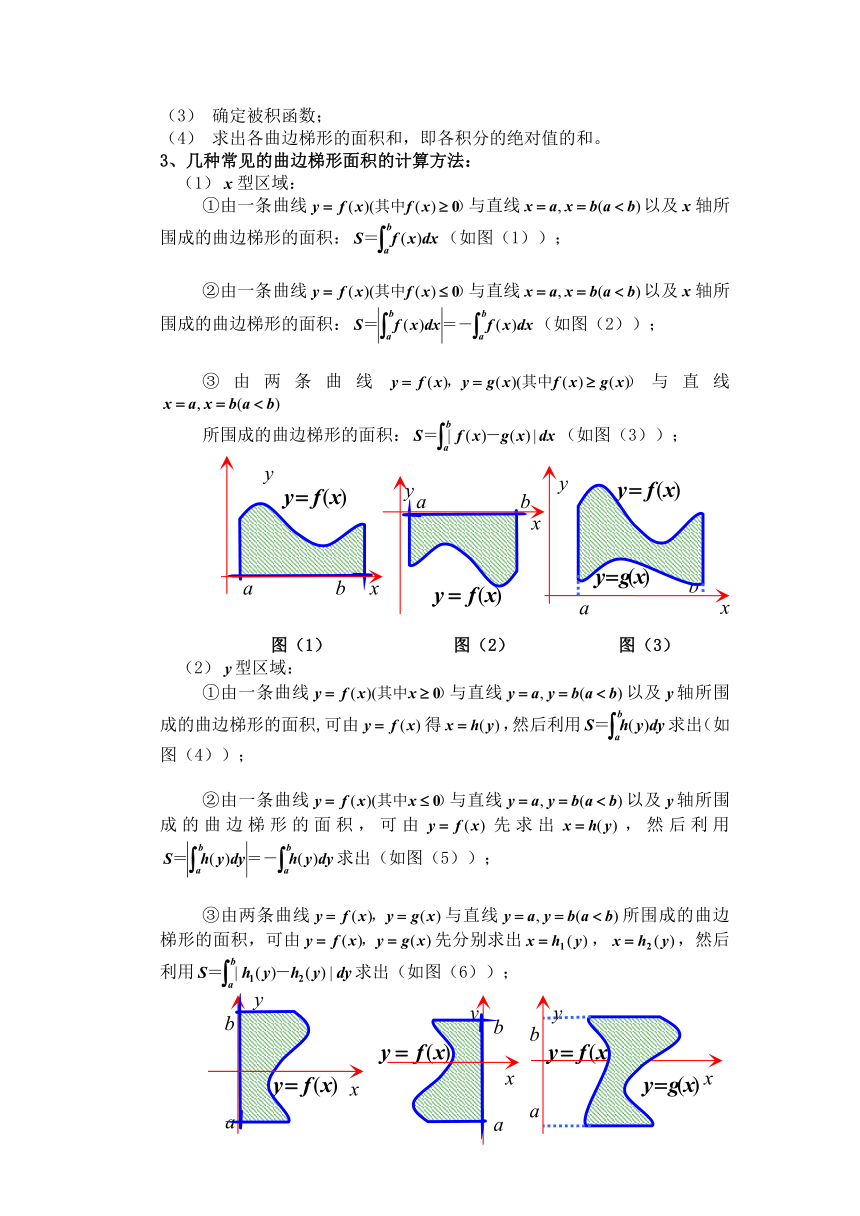
①由一条曲线与直线以及轴所围成的曲边梯形的面积:(如图(1));
②由一条曲线与直线以及轴所围成的曲边梯形的面积:(如图(2));
③由两条曲线与直线
所围成的曲边梯形的面积:(如图(3));
图(1)
图(2)
图(3)
(2)型区域:
①由一条曲线与直线以及轴所围成的曲边梯形的面积,可由得,然后利用求出(如图(4));
②由一条曲线与直线以及轴所围成的曲边梯形的面积,可由先求出,然后利用求出(如图(5));
③由两条曲线与直线所围成的曲边梯形的面积,可由先分别求出,,然后利用求出(如图(6));
图(4)
图(5)
图(6)
2.求平面曲线的弧长
设曲线AB方程为,函数在区间上可导,且连续,则曲线AB的弧长为
.
3.求旋转体的体积和侧面积
( http: / / www.21cnjy.com )
由曲线,直线及轴所围成的曲边梯形绕轴旋转而成的旋转体体积为
.
其侧面积为
.
四:课堂小结
本节课主要学习了利用定积分求一些
( http: / / www.21cnjy.com )曲边图形的面积与体积,即定积分在几何中应用,要掌握几种常见图形面积的求法,并且要注意定积分的几何意义,不能等同于图形的面积,要注意微积分的基本思想的应用与理解。
教后感:
20
年
月
日
第
课时
课题:
§1.7
定积分的简单应用(二)
教学目的
1、知识与技能:进一步让学生深刻体会“
( http: / / www.21cnjy.com )分割、以直代曲、求和、逼近”求曲边梯形的思想方法;让学生深刻理解定积分的几何意义以及微积分的基本定理;初步掌握利用定积分求曲边梯形的几种常见题型及方法;体会定积分在物理中应用(变速直线运动的路程、变力沿直线做功)。2、过程与方法:
借助于几何直观定积分的基本思想,了解定积分在实际中的应用3、情感、态度与价值观:
通过定积分在几何和物理中的应用,进一步感受极限的思想
重
点
定积分在几何和物理中的应用
难
点
定积分在几何和物理中的应用
教学过程:
定积分在物理中应用
(1)求变速直线运动的路程
我们知道,作变速直线运动的物体所经过的路程s,等于其速度函数v=v
(t)
(
v(t)
≥0)
在时间区间[a,b]上的定积分,即
例
4。一辆汽车的速度一时间曲线如图1.7
一3
所示.求汽车在这1
min
行驶的路程.
解:由速度一时间曲线可知:
因此汽车在这
1
min
行驶的路程是:
答:汽车在这
1
min
行驶的路程是
1350m
.
(2).变力作功
一物体在恒力F(单位:N)的作用下做直线运动,如果物体沿着与F相同的方向移(单位:m),则力F所作的功为W=Fs
.
探究
如果物体在变力
F(x)的作用下做
( http: / / www.21cnjy.com )直线运动,并且物体沿着与
F
(x)
相同的方向从x
=a
移动到x=b
(a,那么如何计算变力F(x)所作的功W呢?
与求曲边梯形的面积和求变速直线运动的路程一样,可以用“四步曲”解决变力作功问题.可以得到
例5.如图1·7一4
,在弹性限度内,将一弹簧从平衡位置拉到离平衡位置lm
处,求克服弹力所作的功.
( http: / / www.21cnjy.com )
解:在弹性限度内,拉伸(或压缩)弹簧所需的力
F
(
x
)与弹簧拉伸(或压缩)的长度
x
成正比,即
F
(
x
)=
kx
,
其中常数
k
是比例系数.
由变力作功公式,得到
答:克服弹力所作的功为.
例6.A、B两站相距7.2km,一
( http: / / www.21cnjy.com )辆电车从A站B开往站,电车开出ts后到达途中C点,这一段的速度为1.2t(m/s),到C点的速度为24m/s,从C点到B点前的D点以等速行驶,从D点开始刹车,经ts后,速度为(24-1.2t)m/s,在B点恰好停车,试求
(1)A、C间的距离;(2)B、D间的距离;(3)电车从A站到B站所需的时间。
分析:作变速直线运动的物体所经过的路程s,等于其速度函数v=v(t)(v(t)≥0)在时间区间[a,b]上的定积分,即
略解:(1)设A到C的时间为t1则1.2t=24,
t1=20(s),则AC=
(2)设D到B的时间为t21则24-1.2t2=0,
t21=20(s),
则DB=
(3)CD=7200-2240=6720(m),则从C到D的时间为280(s),则所求时间为20+280+20=320(s)。
练习:1:如果1N能拉长弹簧1cm,为了将弹簧拉长6cm,需做功(
A
)
A
0.18J
B
0.26J
C
0.12J
D
0.28J
略解:设,则由题可得,所以做功就是求定积分
四:课堂小结
本节课主要学习了定积分在物理学中的
( http: / / www.21cnjy.com )应用,要掌握几种常见图形面积的求法,并且要注意定积分的几何意义,不能等同于图形的面积,要注意微积分的基本思想的应用与理解。
教后感:
A
B
C
D
O
x
x
O
y=x2
A
B
C
y
a
b
x
y
a
b
x
y
a
b
x
y
a
b
x
y
a
b
x
y
a
b
x
年
月
日
第
课时
课题:
1.7定积分的简单应用(一)
教学目的
1、知识与技能:进一步让学生深刻体会“分割
( http: / / www.21cnjy.com )、以直代曲、求和、逼近”求曲边梯形的思想方法;让学生深刻理解定积分的几何意义以及微积分的基本定理;初步掌握利用定积分求曲边梯形的几种常见题型及方法;体会定积分在物理中应用(变速直线运动的路程、变力沿直线做功)。2、过程与方法:
借助于几何直观定积分的基本思想,了解定积分在实际中的应用3、情感、态度与价值观:
通过定积分在几何和物理中的应用,进一步感受极限的思想
重
点
定积分在几何和物理中的应用
难
点
定积分在几何和物理中的应用
教学过程:
定积分的应用
(一)利用定积分求平面图形的面积
例1.计算由两条抛物线和所围成的图形的面积.
解:,所以两曲线的交点为(0,0)、(1,1),面积S=,所以=
例2.计算由直线,曲线以及x轴所围图形的面积S.
解:作出直线,曲线的草图,所求面积为图阴影部分的面积.
解方程组
得直线与曲线的交点的坐标为(8,4)
.
直线与x轴的交点为(4,0).
因此,所求图形的面积为S=S1+S2
.
例3.求曲线与直线轴所围成的图形面积。
答案:
练习
1、求直线与抛物线所围成的图形面积。
答案:
2、求由抛物线及其在点M(0,-3)和N(3,0)处的两条切线所围成的图形的面积。
略解:,切线方程分别为、
,则所求图形的面积为
3、求曲线与曲线以及轴所围成的图形面积。
略解:所求图形的面积为
4、在曲线上的某点A处作一切线使之与曲线以及轴所围成的面积为.试求:切点A的坐标以及切线方程.
略解:如图由题可设切点坐标为,则切线方程
为,切线与轴的交点坐标为
,则由题可知有
,所以切点坐标与切线方程分别为
总结:
1、定积分的几何意义是:、轴所围成的图形的面积的代数和,即.
2、求曲边梯形面积的方法与步骤:
画图,并将图形分割为若干个曲边梯形;
对每个曲边梯形确定其存在的范围,从而确定积分的上、下限;
确定被积函数;
求出各曲边梯形的面积和,即各积分的绝对值的和。
3、几种常见的曲边梯形面积的计算方法:
(1)型区域:
①由一条曲线与直线以及轴所围成的曲边梯形的面积:(如图(1));
②由一条曲线与直线以及轴所围成的曲边梯形的面积:(如图(2));
③由两条曲线与直线
所围成的曲边梯形的面积:(如图(3));
图(1)
图(2)
图(3)
(2)型区域:
①由一条曲线与直线以及轴所围成的曲边梯形的面积,可由得,然后利用求出(如图(4));
②由一条曲线与直线以及轴所围成的曲边梯形的面积,可由先求出,然后利用求出(如图(5));
③由两条曲线与直线所围成的曲边梯形的面积,可由先分别求出,,然后利用求出(如图(6));
图(4)
图(5)
图(6)
2.求平面曲线的弧长
设曲线AB方程为,函数在区间上可导,且连续,则曲线AB的弧长为
.
3.求旋转体的体积和侧面积
( http: / / www.21cnjy.com )
由曲线,直线及轴所围成的曲边梯形绕轴旋转而成的旋转体体积为
.
其侧面积为
.
四:课堂小结
本节课主要学习了利用定积分求一些
( http: / / www.21cnjy.com )曲边图形的面积与体积,即定积分在几何中应用,要掌握几种常见图形面积的求法,并且要注意定积分的几何意义,不能等同于图形的面积,要注意微积分的基本思想的应用与理解。
教后感:
20
年
月
日
第
课时
课题:
§1.7
定积分的简单应用(二)
教学目的
1、知识与技能:进一步让学生深刻体会“
( http: / / www.21cnjy.com )分割、以直代曲、求和、逼近”求曲边梯形的思想方法;让学生深刻理解定积分的几何意义以及微积分的基本定理;初步掌握利用定积分求曲边梯形的几种常见题型及方法;体会定积分在物理中应用(变速直线运动的路程、变力沿直线做功)。2、过程与方法:
借助于几何直观定积分的基本思想,了解定积分在实际中的应用3、情感、态度与价值观:
通过定积分在几何和物理中的应用,进一步感受极限的思想
重
点
定积分在几何和物理中的应用
难
点
定积分在几何和物理中的应用
教学过程:
定积分在物理中应用
(1)求变速直线运动的路程
我们知道,作变速直线运动的物体所经过的路程s,等于其速度函数v=v
(t)
(
v(t)
≥0)
在时间区间[a,b]上的定积分,即
例
4。一辆汽车的速度一时间曲线如图1.7
一3
所示.求汽车在这1
min
行驶的路程.
解:由速度一时间曲线可知:
因此汽车在这
1
min
行驶的路程是:
答:汽车在这
1
min
行驶的路程是
1350m
.
(2).变力作功
一物体在恒力F(单位:N)的作用下做直线运动,如果物体沿着与F相同的方向移(单位:m),则力F所作的功为W=Fs
.
探究
如果物体在变力
F(x)的作用下做
( http: / / www.21cnjy.com )直线运动,并且物体沿着与
F
(x)
相同的方向从x
=a
移动到x=b
(a
与求曲边梯形的面积和求变速直线运动的路程一样,可以用“四步曲”解决变力作功问题.可以得到
例5.如图1·7一4
,在弹性限度内,将一弹簧从平衡位置拉到离平衡位置lm
处,求克服弹力所作的功.
( http: / / www.21cnjy.com )
解:在弹性限度内,拉伸(或压缩)弹簧所需的力
F
(
x
)与弹簧拉伸(或压缩)的长度
x
成正比,即
F
(
x
)=
kx
,
其中常数
k
是比例系数.
由变力作功公式,得到
答:克服弹力所作的功为.
例6.A、B两站相距7.2km,一
( http: / / www.21cnjy.com )辆电车从A站B开往站,电车开出ts后到达途中C点,这一段的速度为1.2t(m/s),到C点的速度为24m/s,从C点到B点前的D点以等速行驶,从D点开始刹车,经ts后,速度为(24-1.2t)m/s,在B点恰好停车,试求
(1)A、C间的距离;(2)B、D间的距离;(3)电车从A站到B站所需的时间。
分析:作变速直线运动的物体所经过的路程s,等于其速度函数v=v(t)(v(t)≥0)在时间区间[a,b]上的定积分,即
略解:(1)设A到C的时间为t1则1.2t=24,
t1=20(s),则AC=
(2)设D到B的时间为t21则24-1.2t2=0,
t21=20(s),
则DB=
(3)CD=7200-2240=6720(m),则从C到D的时间为280(s),则所求时间为20+280+20=320(s)。
练习:1:如果1N能拉长弹簧1cm,为了将弹簧拉长6cm,需做功(
A
)
A
0.18J
B
0.26J
C
0.12J
D
0.28J
略解:设,则由题可得,所以做功就是求定积分
四:课堂小结
本节课主要学习了定积分在物理学中的
( http: / / www.21cnjy.com )应用,要掌握几种常见图形面积的求法,并且要注意定积分的几何意义,不能等同于图形的面积,要注意微积分的基本思想的应用与理解。
教后感:
A
B
C
D
O
x
x
O
y=x2
A
B
C
y
a
b
x
y
a
b
x
y
a
b
x
y
a
b
x
y
a
b
x
y
a
b
x
