图形的全等
图片预览






文档简介
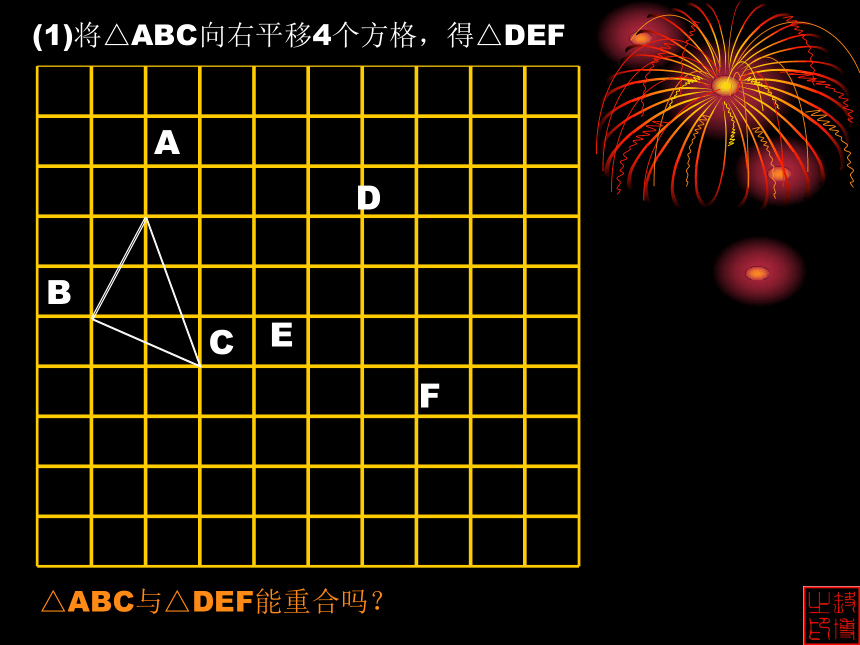
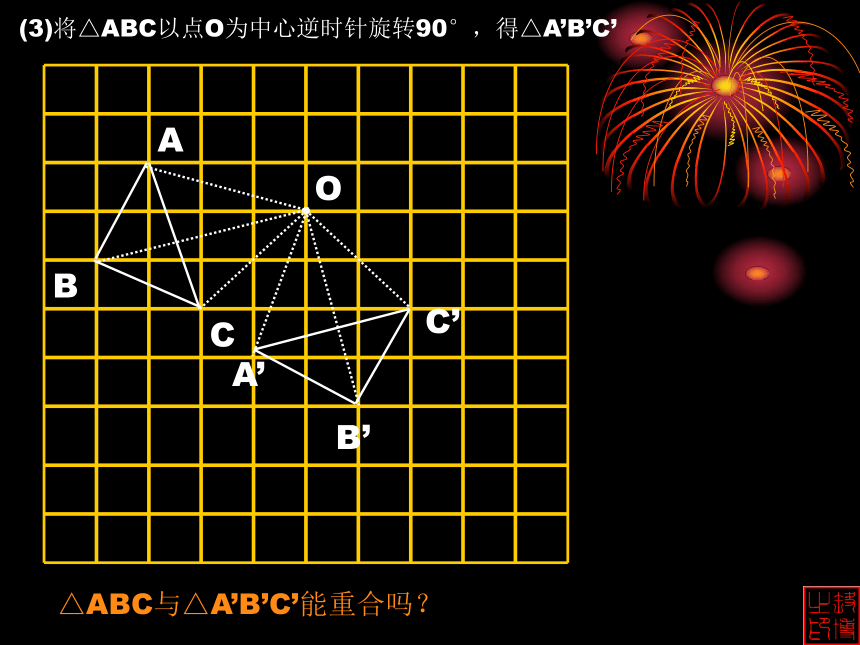
课件20张PPT。初二数学 15.4 图形的全等DEF△ABC与△DEF能重合吗?(1)将△ABC向右平移4个方格,得△DEFDEF(2)作△ABC关于直线l 的对称图形,得△DEF△ABC与△DEF能重合吗?A’B’C’△ABC与△A’B’C’能重合吗?(3)将△ABC以点O为中心逆时针旋转90°,得△A’B’C’以上都是由一个图形通过平移、翻折、旋转得到的新图形能与原图完全重合,
我们把这种归纳:能完全重合的两个图形,叫做全等图形全等图形定义:能够完全重合的图形称为全等图形想一想: 如果两个图形全等,它们
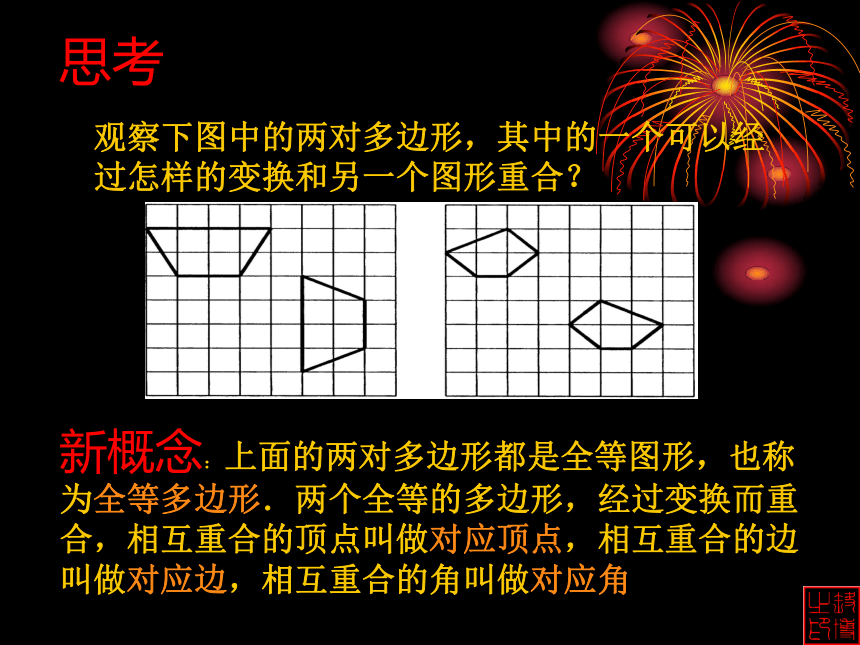
的形状与大小一定相同吗?全等图形的形状与大小都相同观察下图中的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合?思考新概念:上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角 ABCDEA1B1C1D1E1五边形ABCDE 五边形A1B1C1D1E1s= 对应边全等多边形:能够完全重合的多边形AB A1B1BC B1C1CD C1D1DE D1E1EA E1A1=====对应角∠A ∠A1 ∠B ∠B1 ∠C ∠C1 ∠D ∠D1 ∠E ∠E1=====全等于全等多边形的对应边、对应角分别相等. 实际上这也是我们判定全等多边形的方法,即________________________的两个多边形全等. 对应边、对应角都分别相等全等图形的形状与大小都相同全等多边形的性质:全等多边形的对应边、对应角分别相等全等多边形的判定方法:如果两个多边形的边、角分别对应相等,那么这两个多边形全等。全等三角形的性质:全等三角形的对应边、对应角分别相等全等三角形的判定方法:如果两个三角形的边、角分别对应相等,那么这两个三角形全等。说一说概念介绍能够完全重合的两个三角形叫做全等三角形。两个全等三角形经过变换而重合时
互相重合的顶点叫
互相重合的边叫做
互相重合的角叫做点A与点A′.点B与B′.点C与点C′对应顶点:对 应 边:对 应 角:对应顶点对应边对应角ABCAB与A′B′.AC与A′C′.CB与C′B′∠A与∠A′.∠B与∠B′.∠C与∠C′小结寻找对应元素的规律(1)有公共边的,公共边 是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最长的边是对应边,最短的边是对应边;
(5)两个全等三角形最大的角是对应角,最小的角是对应角;表示方法:记作:△ABC △ A′B′C′≌如图15.4.4中的两个三角形是全等的 图15.4.4※ 记两个全等三角形时,通常把表示对应顶点的字母写在对应的位置上。它读作“全等于”!一定要记住哦!全等三角形的对应边相等,
对应角相等。 ∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE
( )
∴ ∠ A= ∠ D, ∠ B= ∠ F ,
∠ C= ∠ E
( )全等三角形的性质应用全等三角形的对应边相等全等三角形的对应角相等1、能够 的两个图形叫全等图形;
2、两个全等三角形重合时,互相重合的顶点叫做 ; 互相重合的边叫做 ;互相重合的角叫做 ;
3、全等三角形对应边 ,对应角 ;
4、记两个三角形全等时,通常把表示对应顶点的字母写在 ;例如△ABC≌ △DFE ,对应顶点分别是
;
5、两个三角形全等时,对应顶点所在的角是 ,对 应角所对的边是 ,对应边所对的角是 。 完全重合对应顶点对应边对应角相等相等对应位置点A和点D、点B和点F、点C和点E对应边对应角对应角 考考你:已知△ABC≌△DEF, △ ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度。解:∵ △ABC≌△DEF (已知) ∴AC=DF。(全等三角形的对应边相等) ∵△ABC的周长是40cm, AB=10cm,BC=16cm, (已知) ∴ AC=40-10-16=14(cm), ∴ DF=14cm。脑筋动多多方法想多多 ABCDEF 如图△ ABD ≌ △CDB,若AB=4,AD=5,BD=6,则BC= ,CD= 。达标测试54如图, △ABC绕AC翻折得△AEC, ∠B=30°,∠ACB=85°,求出△AEC各角的度数。因此 △ AEC的内角度数分别为65°﹑30°﹑85°。BCEA解:在△ABC中∠ACB=85°,∠B=30°,
所以∠BAC=65°又因为△AEC 由△ABC 翻折得到
所以△ABC≌△AEC,
即有∠EAC=∠BAC=65°,
∠E=∠B=30°,
∠ACE=∠ACB=85°应用提高1、什么是全等图形2、多边形全等的特征 ? 今天你学到了什么 ? 能完全重合的两个图形叫做全等图形.特别是研究多边形(三角形)的全等对应边相等、对应角相等如果两个多边形的边都对应相等、角都对应相等,那第这两个多边形全等.3、识别多边形全等的方法
我们把这种归纳:能完全重合的两个图形,叫做全等图形全等图形定义:能够完全重合的图形称为全等图形想一想: 如果两个图形全等,它们
的形状与大小一定相同吗?全等图形的形状与大小都相同观察下图中的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合?思考新概念:上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角 ABCDEA1B1C1D1E1五边形ABCDE 五边形A1B1C1D1E1s= 对应边全等多边形:能够完全重合的多边形AB A1B1BC B1C1CD C1D1DE D1E1EA E1A1=====对应角∠A ∠A1 ∠B ∠B1 ∠C ∠C1 ∠D ∠D1 ∠E ∠E1=====全等于全等多边形的对应边、对应角分别相等. 实际上这也是我们判定全等多边形的方法,即________________________的两个多边形全等. 对应边、对应角都分别相等全等图形的形状与大小都相同全等多边形的性质:全等多边形的对应边、对应角分别相等全等多边形的判定方法:如果两个多边形的边、角分别对应相等,那么这两个多边形全等。全等三角形的性质:全等三角形的对应边、对应角分别相等全等三角形的判定方法:如果两个三角形的边、角分别对应相等,那么这两个三角形全等。说一说概念介绍能够完全重合的两个三角形叫做全等三角形。两个全等三角形经过变换而重合时
互相重合的顶点叫
互相重合的边叫做
互相重合的角叫做点A与点A′.点B与B′.点C与点C′对应顶点:对 应 边:对 应 角:对应顶点对应边对应角ABCAB与A′B′.AC与A′C′.CB与C′B′∠A与∠A′.∠B与∠B′.∠C与∠C′小结寻找对应元素的规律(1)有公共边的,公共边 是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最长的边是对应边,最短的边是对应边;
(5)两个全等三角形最大的角是对应角,最小的角是对应角;表示方法:记作:△ABC △ A′B′C′≌如图15.4.4中的两个三角形是全等的 图15.4.4※ 记两个全等三角形时,通常把表示对应顶点的字母写在对应的位置上。它读作“全等于”!一定要记住哦!全等三角形的对应边相等,
对应角相等。 ∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE
( )
∴ ∠ A= ∠ D, ∠ B= ∠ F ,
∠ C= ∠ E
( )全等三角形的性质应用全等三角形的对应边相等全等三角形的对应角相等1、能够 的两个图形叫全等图形;
2、两个全等三角形重合时,互相重合的顶点叫做 ; 互相重合的边叫做 ;互相重合的角叫做 ;
3、全等三角形对应边 ,对应角 ;
4、记两个三角形全等时,通常把表示对应顶点的字母写在 ;例如△ABC≌ △DFE ,对应顶点分别是
;
5、两个三角形全等时,对应顶点所在的角是 ,对 应角所对的边是 ,对应边所对的角是 。 完全重合对应顶点对应边对应角相等相等对应位置点A和点D、点B和点F、点C和点E对应边对应角对应角 考考你:已知△ABC≌△DEF, △ ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度。解:∵ △ABC≌△DEF (已知) ∴AC=DF。(全等三角形的对应边相等) ∵△ABC的周长是40cm, AB=10cm,BC=16cm, (已知) ∴ AC=40-10-16=14(cm), ∴ DF=14cm。脑筋动多多方法想多多 ABCDEF 如图△ ABD ≌ △CDB,若AB=4,AD=5,BD=6,则BC= ,CD= 。达标测试54如图, △ABC绕AC翻折得△AEC, ∠B=30°,∠ACB=85°,求出△AEC各角的度数。因此 △ AEC的内角度数分别为65°﹑30°﹑85°。BCEA解:在△ABC中∠ACB=85°,∠B=30°,
所以∠BAC=65°又因为△AEC 由△ABC 翻折得到
所以△ABC≌△AEC,
即有∠EAC=∠BAC=65°,
∠E=∠B=30°,
∠ACE=∠ACB=85°应用提高1、什么是全等图形2、多边形全等的特征 ? 今天你学到了什么 ? 能完全重合的两个图形叫做全等图形.特别是研究多边形(三角形)的全等对应边相等、对应角相等如果两个多边形的边都对应相等、角都对应相等,那第这两个多边形全等.3、识别多边形全等的方法
