第1、2章 电磁感应 楞次定律和自感现象 课件
文档属性
| 名称 | 第1、2章 电磁感应 楞次定律和自感现象 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-08-15 08:43:49 | ||
图片预览








文档简介
课件22张PPT。第1、2章 电磁感应 楞次定律和自感现象体系构建1.楞次定律的应用规律
(1)阻碍原磁通量的变化——增反减同
(2)阻碍物体间的相对运动——来拒去留
(3)阻碍回路面积的变化——增缩减扩
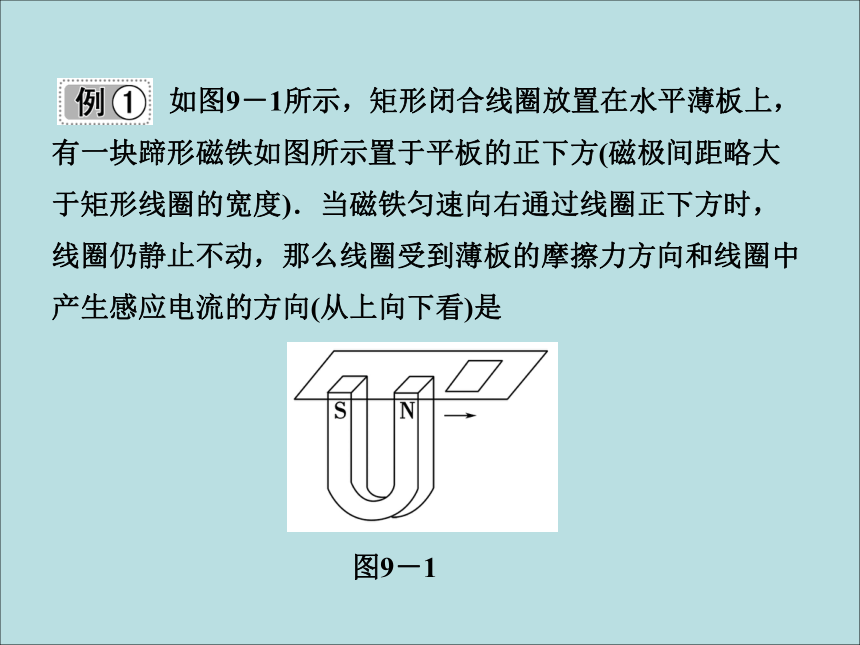
(4)阻碍自身电流的变化——增反减同方法总结 如图9-1所示,矩形闭合线圈放置在水平薄板上,有一块蹄形磁铁如图所示置于平板的正下方(磁极间距略大于矩形线圈的宽度).当磁铁匀速向右通过线圈正下方时,线圈仍静止不动,那么线圈受到薄板的摩擦力方向和线圈中产生感应电流的方向(从上向下看)是图9-1A.摩擦力方向一直向左
B.摩擦力方向先向左、后向右
C.感应电流的方向顺时针→逆时针→逆时针→顺时针
D.感应电流的方向顺时针→逆时针
【解析】 根据蹄形磁铁的磁场特点,可以把磁铁匀速向右通过线圈的过程分为4个阶段:(1)N极靠近线圈→N极处于线圈正中央,线圈中的磁通量向上并增加;(2)N极处于线圈正中央→线圈处于N极与S极正中央,该过程线圈中的磁通量向上并减小到零;(3)线圈处于N极与S极正中央→S极处于线圈正中央,该过程线圈中的磁通量向下并增加;
(4)S极处于线圈正中央→S极离开并远离线圈,该过程线圈中的磁通量向下并减小.根据楞次定律不难判断出,这四个阶段线圈中产生的感应电流方向分别是:顺时针→逆时针→逆时针→顺时针.至于线圈的受力情况,可以根据楞次定律的重要推论“感应电流的磁场总是阻碍引起感应电流的相对运动”来判断线圈受到薄板的摩擦力方向一直向左.
【答案】 AC
1.电路问题的求解方法
2.图象问题的求解方法
(1)明确图象的种类.(2)分析电磁感应的具体过程.(3)结合相关规律写出函数表达式.(4)根据函数关系画图象或进行图象分析. 如图9-2所示,水平面上固定一个由均匀金属杆制成的“∠”导轨ACD,θ=37°,匀强磁场的方向与导轨所在平面垂直,磁感应强度B=0.4 T,另一根保持与导轨ACD接触良好,并保持与CD杆垂直.用水平拉力F向右拉动MN,使其从C点起以v=4 m/s的速度向右匀速运动.金属杆和导轨的电阻都是r=0.3 Ω/m,其余电阻忽略不计.试在下面的坐标系中(如图9-3)分别作出F-t图象和I-t图象,标出必要的坐标值.图9-2图9-3【解析】 本题首先应把导体棒的有效切割长度、闭合回路的导线总长度用时间t表示出来,再利用相关公式写出回路中的电流I和拉力F随时间t而变化的关系式,最后再画出相关图象.图象为:
【答案】 略1.动力学问题
(1)首先明确两大研究对象的相互制约的关系:
(2)抓住一个重要特点:在力和运动的关系中,要注意分析导体受力,判断导体加速度方向、大小及变化;加速度等于零时,速度最大,导体最终达到稳定状态是该类问题的重要特点.
(3)列动力学方程或平衡方程求解.2.能量问题
(1)安培力做的功是电能和其他形式的能之间相互转化的“桥梁”,用框图表示如:
(2)在利用能量守恒解决电磁感应中的问题时,除分析安培力做功导致能量转化外,还要注意分析其他力做功引起的能量转化,即参与能量转化的形式要考虑周全,要考虑准确哪些形式的能量增加,哪些形式的能量减少. 如图9-4所示,两根足够长的光滑直金属导轨MN、PQ平行固定在倾角θ=37°的绝缘斜面上,两导轨间距L=1 m,导轨的电阻可忽略.M、P两点间接有阻值为R的电阻.一根质量m=1 kg、电阻r=0.2 Ω的均匀直金属杆ab放在两导轨上,与导轨垂直且接触良好.整套装置处于磁感应强度B=0.5 T的匀强磁场中,磁场方向垂直斜面向下.自图示位置起,杆ab受到大小为F=0.5v+2(式中v为杆ab运动的速度,力F的单位为N)、方向平行导轨沿斜面向下的拉力作用,由静止开始运动,测得通过电阻R的电流随时间均匀增大.g取10 m/s2,sin 37°=0.6.
图9-4
(1)试判断金属杆ab在匀强磁场中做何种运动,并写出推理过程;
(2)求电阻R的阻值;
(3)已知金属杆ab自静止开始下滑x=1 m的过程中,电阻R上产生的焦耳热为Q1=0.8 J,求该过程需要的时间t和拉力F做的功W.
【解析】 (1)金属杆做匀加速运动(或金属杆做初速度为零的匀加速运动).
【答案】 (1)见解析 (2)0.3 Ω
(3)0.5 s J
(1)阻碍原磁通量的变化——增反减同
(2)阻碍物体间的相对运动——来拒去留
(3)阻碍回路面积的变化——增缩减扩
(4)阻碍自身电流的变化——增反减同方法总结 如图9-1所示,矩形闭合线圈放置在水平薄板上,有一块蹄形磁铁如图所示置于平板的正下方(磁极间距略大于矩形线圈的宽度).当磁铁匀速向右通过线圈正下方时,线圈仍静止不动,那么线圈受到薄板的摩擦力方向和线圈中产生感应电流的方向(从上向下看)是图9-1A.摩擦力方向一直向左
B.摩擦力方向先向左、后向右
C.感应电流的方向顺时针→逆时针→逆时针→顺时针
D.感应电流的方向顺时针→逆时针
【解析】 根据蹄形磁铁的磁场特点,可以把磁铁匀速向右通过线圈的过程分为4个阶段:(1)N极靠近线圈→N极处于线圈正中央,线圈中的磁通量向上并增加;(2)N极处于线圈正中央→线圈处于N极与S极正中央,该过程线圈中的磁通量向上并减小到零;(3)线圈处于N极与S极正中央→S极处于线圈正中央,该过程线圈中的磁通量向下并增加;
(4)S极处于线圈正中央→S极离开并远离线圈,该过程线圈中的磁通量向下并减小.根据楞次定律不难判断出,这四个阶段线圈中产生的感应电流方向分别是:顺时针→逆时针→逆时针→顺时针.至于线圈的受力情况,可以根据楞次定律的重要推论“感应电流的磁场总是阻碍引起感应电流的相对运动”来判断线圈受到薄板的摩擦力方向一直向左.
【答案】 AC
1.电路问题的求解方法
2.图象问题的求解方法
(1)明确图象的种类.(2)分析电磁感应的具体过程.(3)结合相关规律写出函数表达式.(4)根据函数关系画图象或进行图象分析. 如图9-2所示,水平面上固定一个由均匀金属杆制成的“∠”导轨ACD,θ=37°,匀强磁场的方向与导轨所在平面垂直,磁感应强度B=0.4 T,另一根保持与导轨ACD接触良好,并保持与CD杆垂直.用水平拉力F向右拉动MN,使其从C点起以v=4 m/s的速度向右匀速运动.金属杆和导轨的电阻都是r=0.3 Ω/m,其余电阻忽略不计.试在下面的坐标系中(如图9-3)分别作出F-t图象和I-t图象,标出必要的坐标值.图9-2图9-3【解析】 本题首先应把导体棒的有效切割长度、闭合回路的导线总长度用时间t表示出来,再利用相关公式写出回路中的电流I和拉力F随时间t而变化的关系式,最后再画出相关图象.图象为:
【答案】 略1.动力学问题
(1)首先明确两大研究对象的相互制约的关系:
(2)抓住一个重要特点:在力和运动的关系中,要注意分析导体受力,判断导体加速度方向、大小及变化;加速度等于零时,速度最大,导体最终达到稳定状态是该类问题的重要特点.
(3)列动力学方程或平衡方程求解.2.能量问题
(1)安培力做的功是电能和其他形式的能之间相互转化的“桥梁”,用框图表示如:
(2)在利用能量守恒解决电磁感应中的问题时,除分析安培力做功导致能量转化外,还要注意分析其他力做功引起的能量转化,即参与能量转化的形式要考虑周全,要考虑准确哪些形式的能量增加,哪些形式的能量减少. 如图9-4所示,两根足够长的光滑直金属导轨MN、PQ平行固定在倾角θ=37°的绝缘斜面上,两导轨间距L=1 m,导轨的电阻可忽略.M、P两点间接有阻值为R的电阻.一根质量m=1 kg、电阻r=0.2 Ω的均匀直金属杆ab放在两导轨上,与导轨垂直且接触良好.整套装置处于磁感应强度B=0.5 T的匀强磁场中,磁场方向垂直斜面向下.自图示位置起,杆ab受到大小为F=0.5v+2(式中v为杆ab运动的速度,力F的单位为N)、方向平行导轨沿斜面向下的拉力作用,由静止开始运动,测得通过电阻R的电流随时间均匀增大.g取10 m/s2,sin 37°=0.6.
图9-4
(1)试判断金属杆ab在匀强磁场中做何种运动,并写出推理过程;
(2)求电阻R的阻值;
(3)已知金属杆ab自静止开始下滑x=1 m的过程中,电阻R上产生的焦耳热为Q1=0.8 J,求该过程需要的时间t和拉力F做的功W.
【解析】 (1)金属杆做匀加速运动(或金属杆做初速度为零的匀加速运动).
【答案】 (1)见解析 (2)0.3 Ω
(3)0.5 s J
同课章节目录
- 第1章 电磁感应
- 导入 改变世界的线圈
- 第1节 磁生电的探索
- 第2节 感应电动势与电磁感应定律
- 第3节 电磁感应定律的应用
- 第2章 楞次定律和自感现象
- 导入 奇异的电火花
- 第1节 感应电流的方向
- 第2节 自感
- 第3节 自感现象的应用
- 专题探究 电磁感应的实验与调研
- 第3章 交变电流
- 导入 两种电源
- 第1节 交变电流的特点
- 第2节 交变电流是怎样产生的
- 第3节 交变电流中的电容和电感
- 第4章 远距离输电
- 导入 电如何到我家
- 第1节 三相交变电流
- 第2节变压器
- 第3节 电能的远距离传输
- 专题探究 交变电流的实验与调研
- 第5章 传感器及其应用
- 导入 从芝麻开门说起
- 第1节 揭开传感器的面纱
- 第2节 常见传感器工作原理
- 第3节 大显身手的传感器
- 专题探究 传感器的实验与调研
