云南省楚雄州普通高中2015-2016学年高二下学期期末考试数学文试题
文档属性
| 名称 | 云南省楚雄州普通高中2015-2016学年高二下学期期末考试数学文试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 122.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-12 00:00:00 | ||
图片预览


文档简介
2016年楚雄州普通高中学年末教学质量检测
高二文科数学试题
(考试时间:120分钟)
第Ⅰ卷(选择题60分)
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
(1)已知集合A={x|﹣1<x<2},B={x|0<x<3},则A∪B=
(A)(﹣1,3)
(B)(﹣1,0)
(C)(0,2)
(D)(2,3)
(2)=
(A)1+2i
(B)﹣1+2i
(C)1﹣2i
(D)﹣1﹣2i
(3)已知命题p、q,“ p为真”是“p∧q为假”的
(A)充分不必要条件
(B)必要不充分条件
(C)充要条件
(D)既不充分也不必要条件
(4)已知=(1,﹣1),=(﹣1,2)则=
(A)﹣1
(B)0
(C)1
(D)2
(5)等差数列{an}的公差为2,若a2,a4,a8成等比数列,则{an}的前10项和S10=
(A)110
(B)99
(C)55
(D)45
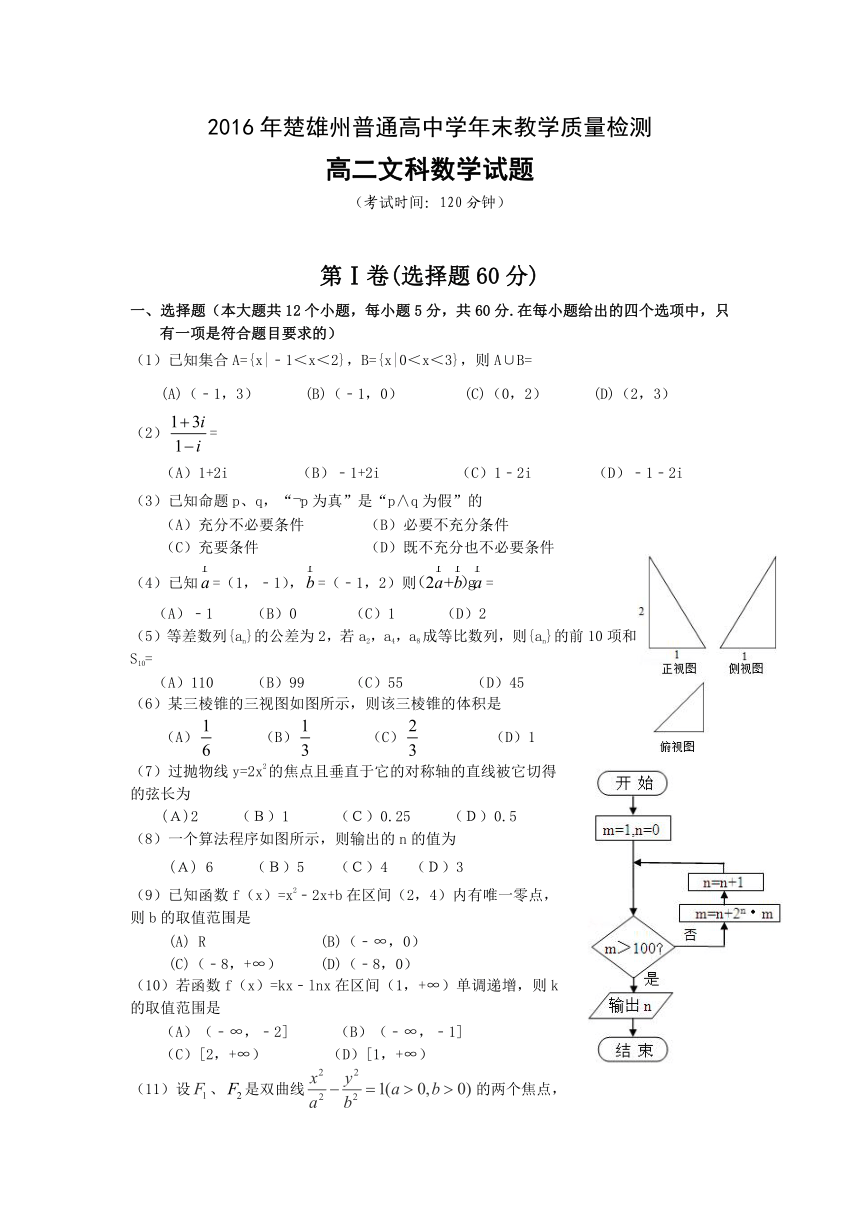
(6)某三棱锥的三视图如图所示,则该三棱锥的体积是
(A)
(B)
(C)
(D)1
(7)过抛物线y=2x2的焦点且垂直于它的对称轴的直线被它切得的弦长为
(A)2
(B)1
(C)0.25
(D)0.5
(8)一个算法程序如图所示,则输出的n的值为
(A)
6
(B)5
(C)4
(D)3
(9)已知函数f(x)=x2﹣2x+b在区间(2,4)内有唯一零点,则b的取值范围是
(A)
R
(B)(﹣∞,0)
(C)(﹣8,+∞)
(D)(﹣8,0)
(10)若函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,则k的取值范围是
(A)(﹣∞,﹣2]
(B)(﹣∞,﹣1]
(C)[2,+∞)
(D)[1,+∞)
(11)设、是双曲线的两个焦点,在双曲线上,若,,则双曲线的离心率为
(A)
(B)
(C)2
(D)
(12)已知函数f(x)是定义在(﹣3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,则不等式f(﹣x)﹒x>0的解集是
(A)(﹣3,﹣1)∪(0,1)
(B)(﹣1,1)
(C)(﹣1,0)∪(0,1)
(D)(﹣1,0)∪(1,3)
第Ⅱ卷(非选择题90分)
二、填空题(本大题共4个小题,每小题5分,共20分.把答案填在题中横线上)
(13)从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是
.
(14)
若x,y满足约束条件,则z=2x+y的最大值为
.
x
y
(15)
已知y与x之间具有很强的线性相关关系,现观测得到(x,y)的四组观测值并制作了相应的对照表,由表中数据粗略地得到线性回归直线方程为y=bx+60,其中的值没有写上.当x=时,预测的值为
.
(16)
在数列{an}中,an=﹣n2+λn,且{an}为递减数列,则λ的取值范围为
.
三、解答题(本大题共70分.解答应写出文字说明,证明过程或演算步骤)
(17)(本小题满分10分)
已知直线的参数方程是(t为参数),圆C的极坐标方程为ρ=2cos(θ+).
(Ⅰ)求圆心C的直角坐标;
(Ⅱ)由直线上的点向圆C引切线,求切线长的最小值.
(18)(本小题满分12分)
已知向量=(cosx,﹣1),=(sinx,﹣),
=(﹣) .
(Ⅰ)求函数f(x)的单调增区间;
(Ⅱ)已知锐角△ABC中角A,B,C的对边分别为a,b,c.其面积S=,,a=3,求b+c的值.
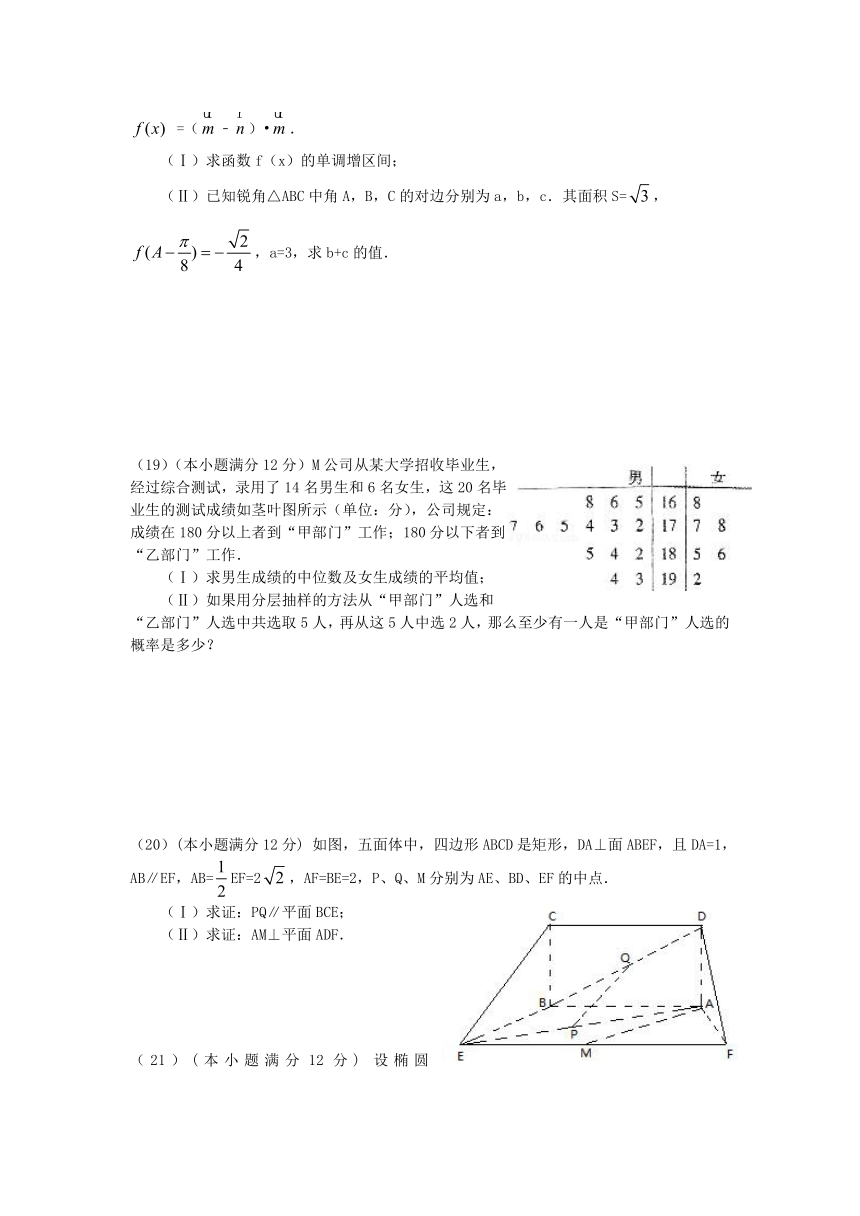
(19)(本小题满分12分)M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
(Ⅰ)求男生成绩的中位数及女生成绩的平均值;
(Ⅱ)如果用分层抽样的方法从“甲部门”人选和“乙部门”人选中共选取5人,再从这5人中选2人,那么至少有一人是“甲部门”人选的概率是多少?
(20)(本小题满分12分)
如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=EF=2,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.
(Ⅰ)求证:PQ∥平面BCE;
(Ⅱ)求证:AM⊥平面ADF.
(21)(本小题满分12分)
设椭圆E:过M、N两点,O为坐标原点.
(I)求椭圆E的方程;
(II)若直线与圆相切,并且与椭圆E相交于两点A、B,求证:.
(22)(本小题满分12分)
已知函数.
(Ⅰ)若=1,求曲线y=在点(1,)处的切线方程;
(Ⅱ)若函数在其定义域内为增函数,求的取值范围;
2016年楚雄州普通高中学年末教学质量检测
高二文科数学试题参考答案与评分标准
一、选择题:本大题共12小题。每小题5分,共60分。
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
答案
A
B
A
C
A
B
D
C
D
D
B
C
二、填空题:本大题共4小题,每小题5分,共20分。
(13)
(14)
8
(15)
70
(16)
(﹣∞,3)
三.解答题:本大题共6个小题,共70分。
(17)
(本小题满分10分)
解:(I)∵,∴,
∴圆C的直角坐标方程为,
即,
∴圆心直角坐标为(5分)。
(II)∵直线l的普通方程为,
圆心C到直线l距离是,
∴直线l上的点向圆C引的切线长的最小值是(10分)。
(18)
(本小题满分12分)
解:(Ⅰ)∵=(cosx,﹣1),=(sinx,﹣),∴﹣=(cosx﹣sinx,),
∴f(x)=(﹣) =(cosx
-
sinx)cosx
-
=
(4分),
由,得,k∈Z。
所以函数的单调性递增区间为:,k∈Z(6分)。
(Ⅱ)∵,
∴,又∵0,∴0<2A<π,∴,即A=(8分),
∴S=,∴bc=4(10分)。
由余弦定理得a2=b2+2﹣2bccos A,∴9=b2+c2﹣bc,∴(b+c)2=b2+c2+2bc=9+3bc=21,
∴b+c=(12分)。
(19)
(本小题满分12分)
解:(Ⅰ)男生共14人,中间两个成绩是175和176,它们的平均数为175.5,
所以男生成绩的中位数是175.5(2分)。
女生的平均成绩==181(4分)
(Ⅱ)用分层抽样的方法从“甲部门”和“乙部门”20人中抽取5人,每个人被抽中的概率是=。根据茎叶图,“甲部门”人选有8人,“乙部门”人选有12人。
所以选中的“甲部门”人选有=2人,“乙部门”人选有=3人(8分)。
记选中的“甲部门”的人员为A1,A2,选中的“乙部门”人员为B,C,D。
从这5人中选2人的所以可能情况为:(A1,A2),(A1,B),(A1,C),(A1,D),(A2,B),(A2,C),(A2,D),(B,C),(B,D),(C,D),共10种。
其中至少有1人是“甲部门”人选的结果有7种。
因此,至少有1人是“甲部门”人选的概率是(12分)。
(20)(本小题满分12分)
证明:(Ⅰ)连接AC.∵四边形ABCD是矩形,Q为BD的中点,∴Q为AC的中点。
又在△AEC中,P为AE的中点,∴PQ∥EC。∵EC 平面BCE,PQ 平面BCE,
∴PQ∥平面BCE(6分)。
(Ⅱ)∵M是EF的中点,∴EM=AB=,
又∵EF∥AB,∴四边形ABEF是平行四边形,
∴AM∥BE,AM=BE=2,又∵AF=2,MF=,
∴AM2+AF2=MF2,∴∠MAF=90°,∴MA⊥AF。
∵DA⊥平面ABEF,∴DA⊥AM。
又∵AF∩AD=A,∴AM⊥平面ADF(12分)
(21)
(本小题满分12分)
解:(I)因为椭圆E:
(a>b>0)过M(2,)
,N(,1)两点,
所以解得所以
,
所以椭圆E的方程为(4分)
(II)设
,由题意得:(6分)
联立,,
所以
所以
==0
。
(12分)
(22)
(本小题满分12分)
解:(Ⅰ)当a=1时,函数,
所以f(1)=1﹣1﹣ln1=0,(4分),
曲线f(x)在点(1,f(1))处的切线的斜率为f′(1)=1+1﹣1=1。
从而曲线f(x)在点(1,f(1))处的切线方程为y﹣0=x﹣1,即y=x﹣1(6分)。
(Ⅱ)(8分)。
要使f(x)在定义域(0,+∞)内是增函数,只需f′(x)≥0
在(0,+∞)内恒成立.即ax2﹣x+a≥0,得恒成立(10分)。
因为,所以,所以。
所以f(x)在(0,+∞)内为增函数,实数a的取值范围是(12分)。
高二文科数学试题
(考试时间:120分钟)
第Ⅰ卷(选择题60分)
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
(1)已知集合A={x|﹣1<x<2},B={x|0<x<3},则A∪B=
(A)(﹣1,3)
(B)(﹣1,0)
(C)(0,2)
(D)(2,3)
(2)=
(A)1+2i
(B)﹣1+2i
(C)1﹣2i
(D)﹣1﹣2i
(3)已知命题p、q,“ p为真”是“p∧q为假”的
(A)充分不必要条件
(B)必要不充分条件
(C)充要条件
(D)既不充分也不必要条件
(4)已知=(1,﹣1),=(﹣1,2)则=
(A)﹣1
(B)0
(C)1
(D)2
(5)等差数列{an}的公差为2,若a2,a4,a8成等比数列,则{an}的前10项和S10=
(A)110
(B)99
(C)55
(D)45
(6)某三棱锥的三视图如图所示,则该三棱锥的体积是
(A)
(B)
(C)
(D)1
(7)过抛物线y=2x2的焦点且垂直于它的对称轴的直线被它切得的弦长为
(A)2
(B)1
(C)0.25
(D)0.5
(8)一个算法程序如图所示,则输出的n的值为
(A)
6
(B)5
(C)4
(D)3
(9)已知函数f(x)=x2﹣2x+b在区间(2,4)内有唯一零点,则b的取值范围是
(A)
R
(B)(﹣∞,0)
(C)(﹣8,+∞)
(D)(﹣8,0)
(10)若函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,则k的取值范围是
(A)(﹣∞,﹣2]
(B)(﹣∞,﹣1]
(C)[2,+∞)
(D)[1,+∞)
(11)设、是双曲线的两个焦点,在双曲线上,若,,则双曲线的离心率为
(A)
(B)
(C)2
(D)
(12)已知函数f(x)是定义在(﹣3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,则不等式f(﹣x)﹒x>0的解集是
(A)(﹣3,﹣1)∪(0,1)
(B)(﹣1,1)
(C)(﹣1,0)∪(0,1)
(D)(﹣1,0)∪(1,3)
第Ⅱ卷(非选择题90分)
二、填空题(本大题共4个小题,每小题5分,共20分.把答案填在题中横线上)
(13)从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是
.
(14)
若x,y满足约束条件,则z=2x+y的最大值为
.
x
y
(15)
已知y与x之间具有很强的线性相关关系,现观测得到(x,y)的四组观测值并制作了相应的对照表,由表中数据粗略地得到线性回归直线方程为y=bx+60,其中的值没有写上.当x=时,预测的值为
.
(16)
在数列{an}中,an=﹣n2+λn,且{an}为递减数列,则λ的取值范围为
.
三、解答题(本大题共70分.解答应写出文字说明,证明过程或演算步骤)
(17)(本小题满分10分)
已知直线的参数方程是(t为参数),圆C的极坐标方程为ρ=2cos(θ+).
(Ⅰ)求圆心C的直角坐标;
(Ⅱ)由直线上的点向圆C引切线,求切线长的最小值.
(18)(本小题满分12分)
已知向量=(cosx,﹣1),=(sinx,﹣),
=(﹣) .
(Ⅰ)求函数f(x)的单调增区间;
(Ⅱ)已知锐角△ABC中角A,B,C的对边分别为a,b,c.其面积S=,,a=3,求b+c的值.
(19)(本小题满分12分)M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
(Ⅰ)求男生成绩的中位数及女生成绩的平均值;
(Ⅱ)如果用分层抽样的方法从“甲部门”人选和“乙部门”人选中共选取5人,再从这5人中选2人,那么至少有一人是“甲部门”人选的概率是多少?
(20)(本小题满分12分)
如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=EF=2,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.
(Ⅰ)求证:PQ∥平面BCE;
(Ⅱ)求证:AM⊥平面ADF.
(21)(本小题满分12分)
设椭圆E:过M、N两点,O为坐标原点.
(I)求椭圆E的方程;
(II)若直线与圆相切,并且与椭圆E相交于两点A、B,求证:.
(22)(本小题满分12分)
已知函数.
(Ⅰ)若=1,求曲线y=在点(1,)处的切线方程;
(Ⅱ)若函数在其定义域内为增函数,求的取值范围;
2016年楚雄州普通高中学年末教学质量检测
高二文科数学试题参考答案与评分标准
一、选择题:本大题共12小题。每小题5分,共60分。
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
答案
A
B
A
C
A
B
D
C
D
D
B
C
二、填空题:本大题共4小题,每小题5分,共20分。
(13)
(14)
8
(15)
70
(16)
(﹣∞,3)
三.解答题:本大题共6个小题,共70分。
(17)
(本小题满分10分)
解:(I)∵,∴,
∴圆C的直角坐标方程为,
即,
∴圆心直角坐标为(5分)。
(II)∵直线l的普通方程为,
圆心C到直线l距离是,
∴直线l上的点向圆C引的切线长的最小值是(10分)。
(18)
(本小题满分12分)
解:(Ⅰ)∵=(cosx,﹣1),=(sinx,﹣),∴﹣=(cosx﹣sinx,),
∴f(x)=(﹣) =(cosx
-
sinx)cosx
-
=
(4分),
由,得,k∈Z。
所以函数的单调性递增区间为:,k∈Z(6分)。
(Ⅱ)∵,
∴,又∵0,∴0<2A<π,∴,即A=(8分),
∴S=,∴bc=4(10分)。
由余弦定理得a2=b2+2﹣2bccos A,∴9=b2+c2﹣bc,∴(b+c)2=b2+c2+2bc=9+3bc=21,
∴b+c=(12分)。
(19)
(本小题满分12分)
解:(Ⅰ)男生共14人,中间两个成绩是175和176,它们的平均数为175.5,
所以男生成绩的中位数是175.5(2分)。
女生的平均成绩==181(4分)
(Ⅱ)用分层抽样的方法从“甲部门”和“乙部门”20人中抽取5人,每个人被抽中的概率是=。根据茎叶图,“甲部门”人选有8人,“乙部门”人选有12人。
所以选中的“甲部门”人选有=2人,“乙部门”人选有=3人(8分)。
记选中的“甲部门”的人员为A1,A2,选中的“乙部门”人员为B,C,D。
从这5人中选2人的所以可能情况为:(A1,A2),(A1,B),(A1,C),(A1,D),(A2,B),(A2,C),(A2,D),(B,C),(B,D),(C,D),共10种。
其中至少有1人是“甲部门”人选的结果有7种。
因此,至少有1人是“甲部门”人选的概率是(12分)。
(20)(本小题满分12分)
证明:(Ⅰ)连接AC.∵四边形ABCD是矩形,Q为BD的中点,∴Q为AC的中点。
又在△AEC中,P为AE的中点,∴PQ∥EC。∵EC 平面BCE,PQ 平面BCE,
∴PQ∥平面BCE(6分)。
(Ⅱ)∵M是EF的中点,∴EM=AB=,
又∵EF∥AB,∴四边形ABEF是平行四边形,
∴AM∥BE,AM=BE=2,又∵AF=2,MF=,
∴AM2+AF2=MF2,∴∠MAF=90°,∴MA⊥AF。
∵DA⊥平面ABEF,∴DA⊥AM。
又∵AF∩AD=A,∴AM⊥平面ADF(12分)
(21)
(本小题满分12分)
解:(I)因为椭圆E:
(a>b>0)过M(2,)
,N(,1)两点,
所以解得所以
,
所以椭圆E的方程为(4分)
(II)设
,由题意得:(6分)
联立,,
所以
所以
==0
。
(12分)
(22)
(本小题满分12分)
解:(Ⅰ)当a=1时,函数,
所以f(1)=1﹣1﹣ln1=0,(4分),
曲线f(x)在点(1,f(1))处的切线的斜率为f′(1)=1+1﹣1=1。
从而曲线f(x)在点(1,f(1))处的切线方程为y﹣0=x﹣1,即y=x﹣1(6分)。
(Ⅱ)(8分)。
要使f(x)在定义域(0,+∞)内是增函数,只需f′(x)≥0
在(0,+∞)内恒成立.即ax2﹣x+a≥0,得恒成立(10分)。
因为,所以,所以。
所以f(x)在(0,+∞)内为增函数,实数a的取值范围是(12分)。
