24.4 弧长和扇形面积
文档属性
| 名称 | 24.4 弧长和扇形面积 |

|
|
| 格式 | rar | ||
| 文件大小 | 288.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-13 00:00:00 | ||
图片预览




文档简介
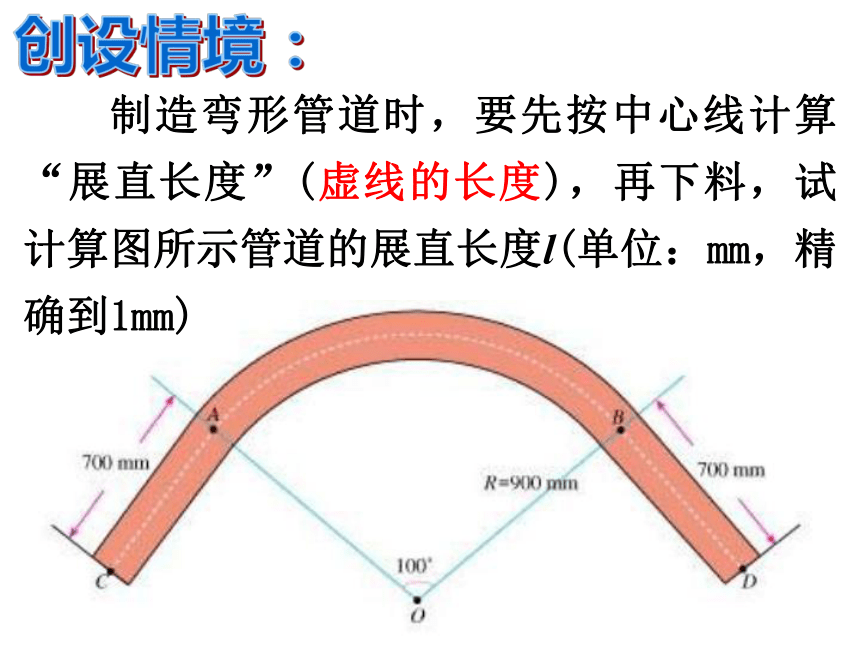
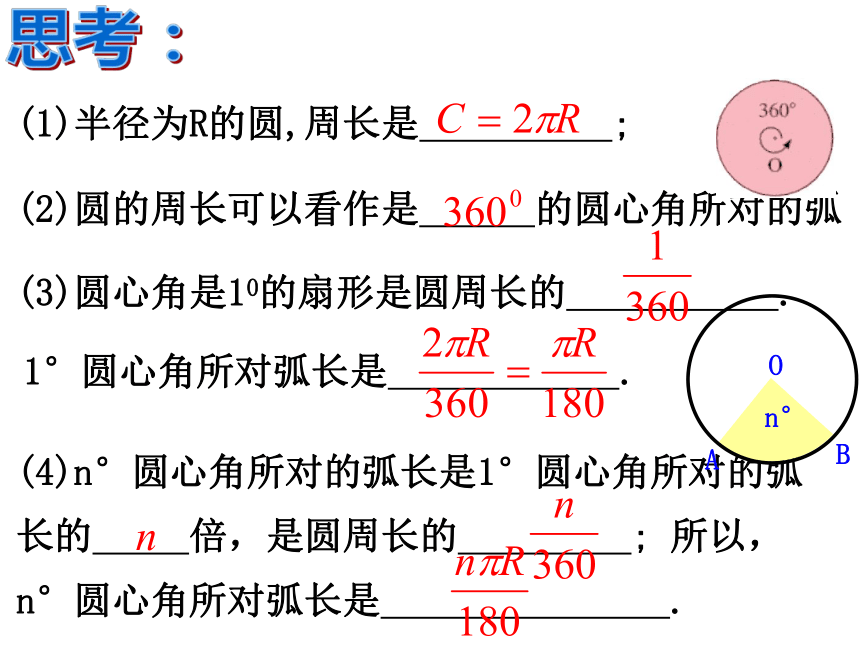
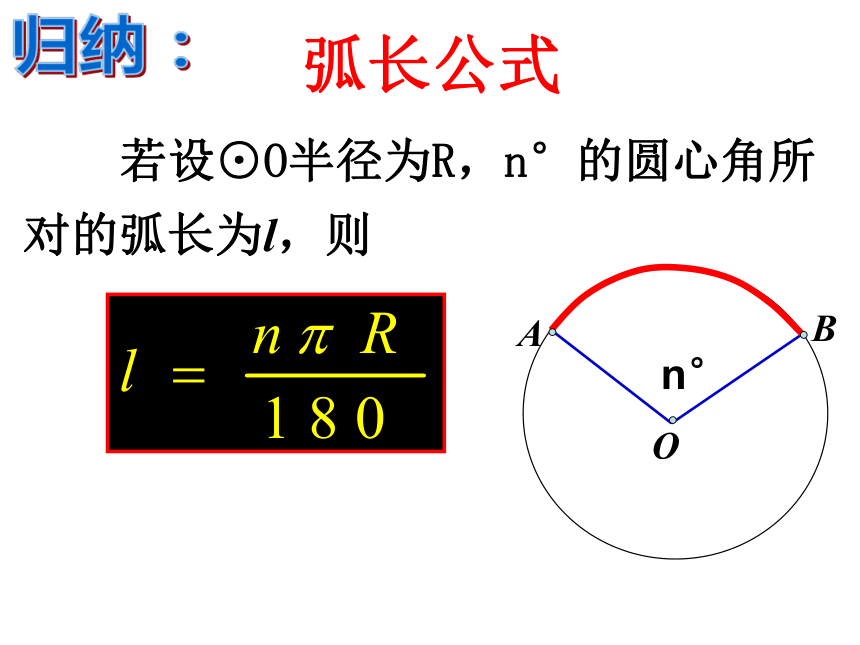
课件22张PPT。24.4 弧长和扇形面积人教版九年级上册 制造弯形管道时,要先按中心线计算“展直长度”(虚线的长度),再下料,试计算图所示管道的展直长度l(单位:mm,精确到1mm)创设情境:(2)圆的周长可以看作是 的圆心角所对的弧(1)半径为R的圆,周长是 ;(3)圆心角是10的扇形是圆周长的 . 思考:1°圆心角所对弧长是 .(4)n°圆心角所对的弧长是1°圆心角所对的弧长的 倍,是圆周长的 ; 所以, n°圆心角所对弧长是 .归纳:弧长公式 若设⊙O半径为R,n°的圆心角所对的弧长为l,则 n°ABO弧长公式1、弧长与哪些因素有关?2、在3个量l、R、n中,只要已知其中两个量就可以求第三个量,那么请将公式变形求出R和n。1.已知弧所对的圆心角为900,半径是4,则弧长为 .
2. 已知一条弧的半径为9,弧长为8 ,那么这条弧所对的圆心角为 .巩固:3. 钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
B.
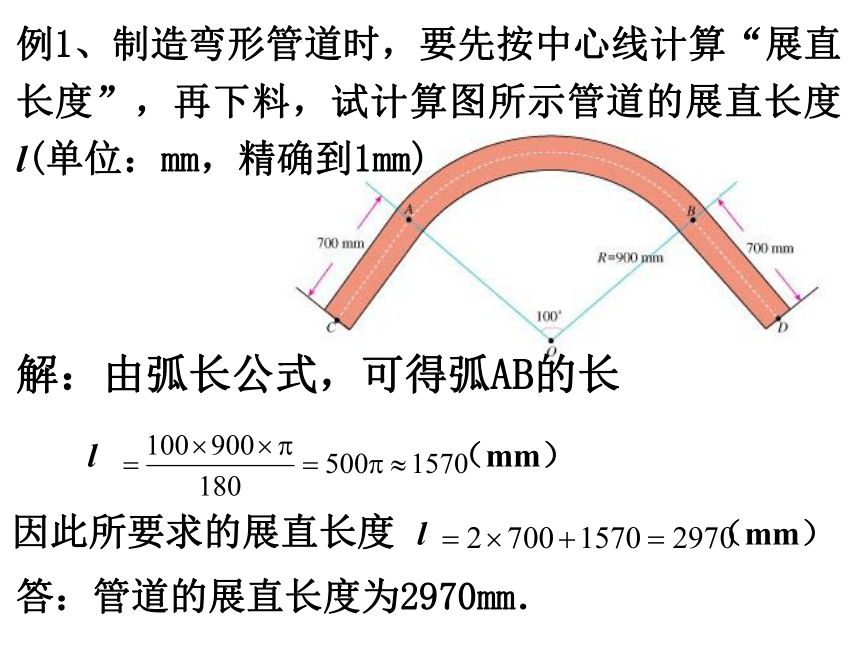
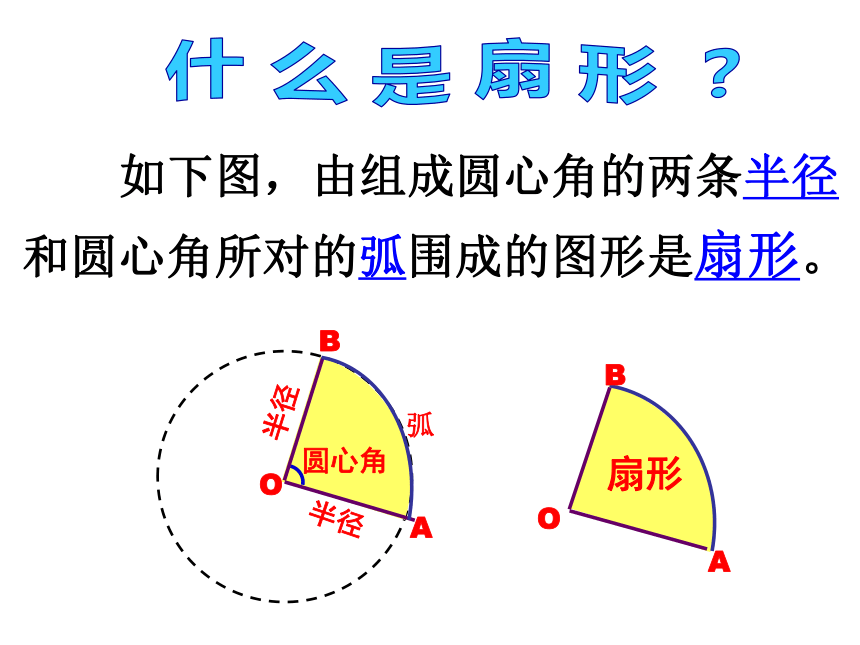
C. D. 巩固:例1、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度l(单位:mm,精确到1mm)解:由弧长公式,可得弧AB的长l (mm) 因此所要求的展直长度 l (mm) 答:管道的展直长度为2970mm. 什 么 是 扇 形 ? 如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。OBA圆心角巩固:(2)圆的面积可以看作是 的圆心角所对的扇形面积;(1)半径为R的圆,面积是 ;(3)圆心角为10的扇形面积是 . 自学教材P111,完成下列内容: 自学提纲2:(4)圆心角为n°的扇形面积是圆心角为1°的扇形面积的 倍,是圆面积的 ; 所以,圆心角是n°的扇形面积是 .归纳:扇形面积公式 若设⊙O半径为R,圆心角为n°的扇形面积为S,则 n°ABO3.已知扇形的圆心角为120°,半径为2,则这个扇形的面积为多少? 巩固:4.已知扇形的半径为3cm,扇形的弧长为πcm,则该扇形的面积是______cm2.巩固:5.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度 .BB1B2问题:扇形的弧长公式与面积公式有联系吗? 想一想:扇形的面积公式与什么公式类似? 如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积S。(精确到0.01cm).CD弓形的面积 = S扇- S△例题:解:如图,连接OA、OB,作弦AB的垂直平分线,垂足为D,交弧AB于点C,连结AC. ∵OC=0.6,DC=0.3 ∴OD=OC-DC=0.30.60.3CD∴OD=DC又∵AD⊥DC ∴AD垂直平分OC∴AC=AO=OC∴∠AOD=600,∠AOB=1200变式:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。ABDCE弓形的面积= S扇+ S△ S弓形=S扇形-S三角形
S弓形=S扇形+S三角形归纳:6、已知正三角形ABC的边长为a,分别以A、B、C为圆心,以0.5a为半径的圆相切于点D、E、F,求图中阴影部分的面积S.7、如图,从P点引⊙O的两切线PA、PB,A、B为切点,已知⊙O的半径为2,∠P=600,则图中阴影部分的面积为 .
2. 已知一条弧的半径为9,弧长为8 ,那么这条弧所对的圆心角为 .巩固:3. 钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
B.
C. D. 巩固:例1、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度l(单位:mm,精确到1mm)解:由弧长公式,可得弧AB的长l (mm) 因此所要求的展直长度 l (mm) 答:管道的展直长度为2970mm. 什 么 是 扇 形 ? 如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。OBA圆心角巩固:(2)圆的面积可以看作是 的圆心角所对的扇形面积;(1)半径为R的圆,面积是 ;(3)圆心角为10的扇形面积是 . 自学教材P111,完成下列内容: 自学提纲2:(4)圆心角为n°的扇形面积是圆心角为1°的扇形面积的 倍,是圆面积的 ; 所以,圆心角是n°的扇形面积是 .归纳:扇形面积公式 若设⊙O半径为R,圆心角为n°的扇形面积为S,则 n°ABO3.已知扇形的圆心角为120°,半径为2,则这个扇形的面积为多少? 巩固:4.已知扇形的半径为3cm,扇形的弧长为πcm,则该扇形的面积是______cm2.巩固:5.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度 .BB1B2问题:扇形的弧长公式与面积公式有联系吗? 想一想:扇形的面积公式与什么公式类似? 如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积S。(精确到0.01cm).CD弓形的面积 = S扇- S△例题:解:如图,连接OA、OB,作弦AB的垂直平分线,垂足为D,交弧AB于点C,连结AC. ∵OC=0.6,DC=0.3 ∴OD=OC-DC=0.30.60.3CD∴OD=DC又∵AD⊥DC ∴AD垂直平分OC∴AC=AO=OC∴∠AOD=600,∠AOB=1200变式:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。ABDCE弓形的面积= S扇+ S△ S弓形=S扇形-S三角形
S弓形=S扇形+S三角形归纳:6、已知正三角形ABC的边长为a,分别以A、B、C为圆心,以0.5a为半径的圆相切于点D、E、F,求图中阴影部分的面积S.7、如图,从P点引⊙O的两切线PA、PB,A、B为切点,已知⊙O的半径为2,∠P=600,则图中阴影部分的面积为 .
同课章节目录
