24.1.1 圆

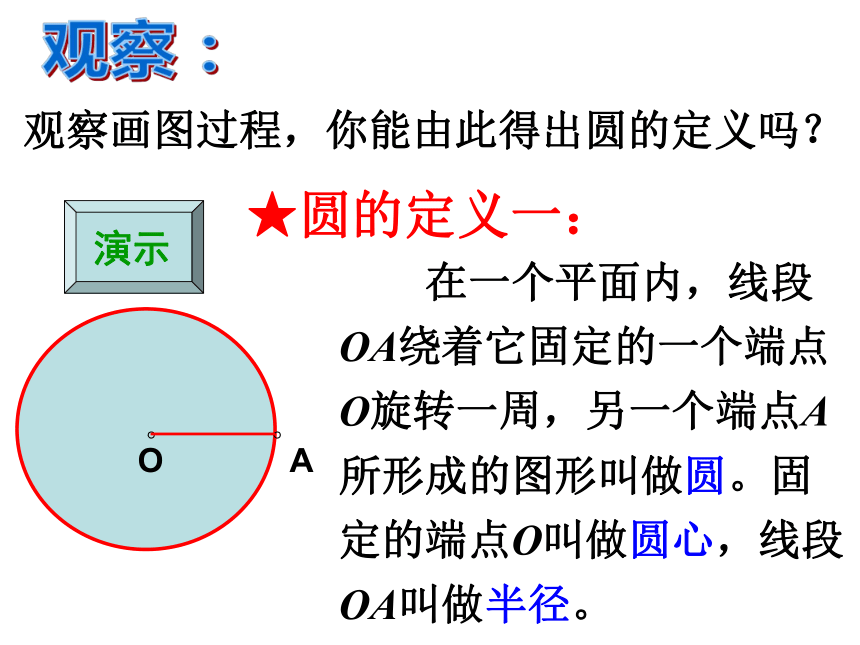
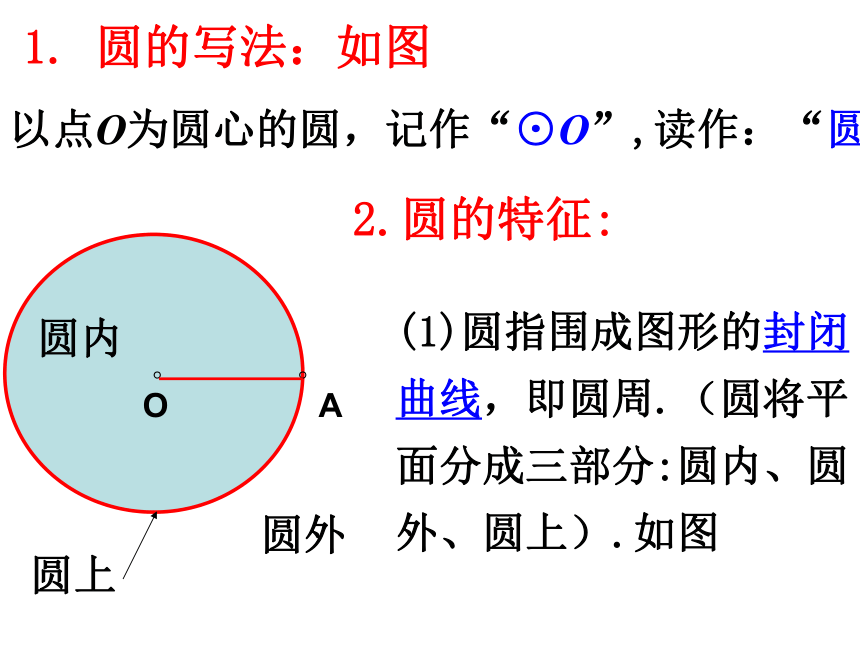
课件25张PPT。24.1.1 圆 人教版九年级上册圆 在一个平面内，线段OA绕着它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆。固定的端点O叫做圆心，线段OA叫做半径。★圆的定义一：观察画图过程，你能由此得出圆的定义吗？观察：1. 圆的写法：如图 2.圆的特征:(1)圆指围成图形的封闭曲线，即圆周.（圆将平面分成三部分:圆内、圆外、圆上）.如图以点O为圆心的圆，记作“⊙O”,读作：“圆O”（2）圆上各点到定点（圆心O）的距离都等于定长（半径r）;（3）到定点的距离等于定
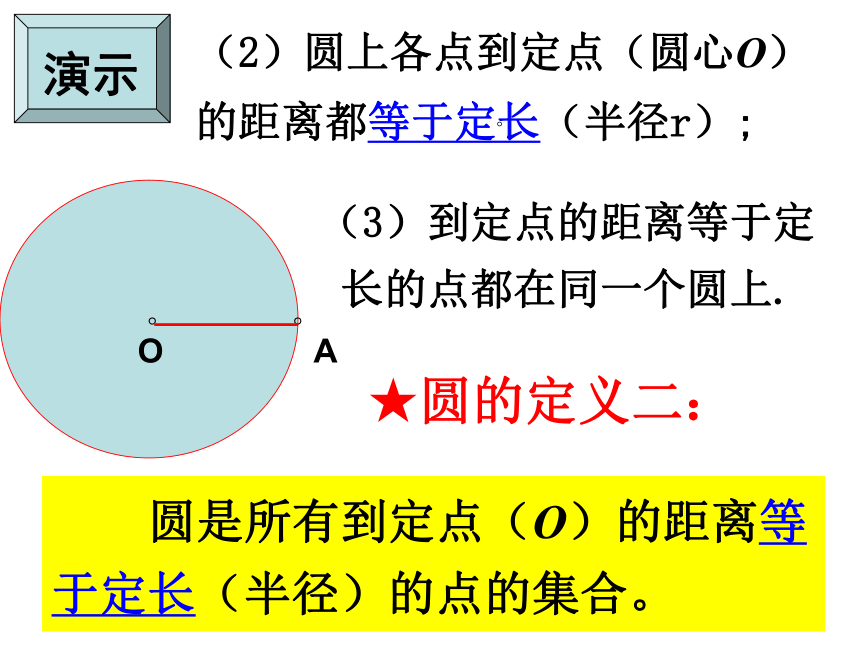
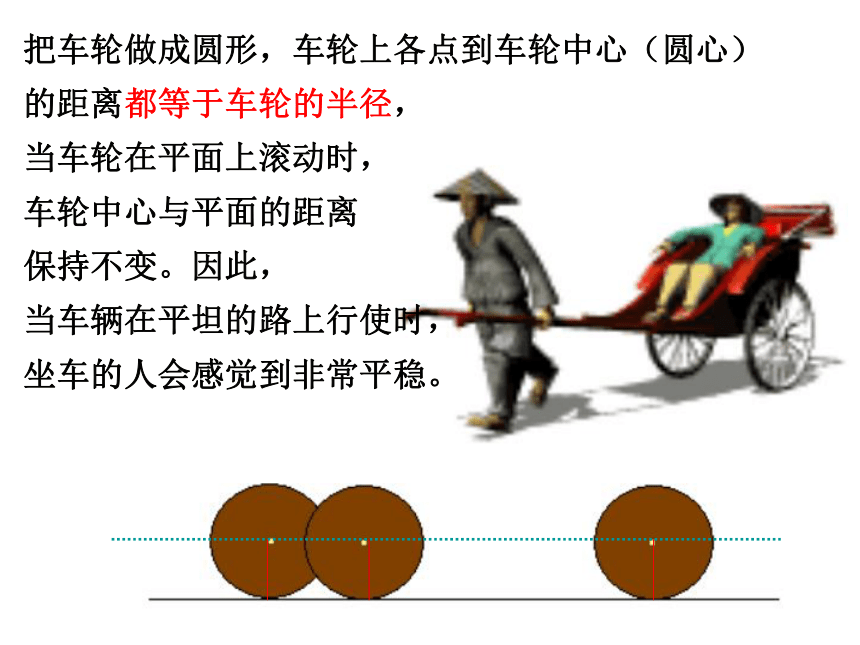
长的点都在同一个圆上.★圆的定义二： 圆是所有到定点（O）的距离等于定长（半径）的点的集合。车轮为什么做成圆形?联系生活把车轮做成圆形，车轮上各点到车轮中心（圆心）
的距离都等于车轮的半径，
当车轮在平面上滚动时，
车轮中心与平面的距离
保持不变。因此，
当车辆在平坦的路上行使时，
坐车的人会感觉到非常平稳。1、以1厘米为半径能画几个圆？这些圆的位置和大小有什么特点？ 圆心不同（位置不同），半径相同（大小相同），这样的两个圆叫做等圆。实践：2、以点O为圆心能画几个圆？这些圆的位置和大小有什么特点？ 圆心相同，但圆的大小不同（半径不同），这样的两个圆叫做同心圆。实践：要确定一个圆,必须确定圆的____和____。 圆心确定圆的位置,半径确定圆的大小.归纳：圆心半径●O·COAB 连接圆上任意两点的线段（如图AC）叫做弦，经过圆心的弦(如图AB)叫做直径．与圆有关的概念：弦CBOAFEDM 问：
（1）FC是弦吗？为什么？
（2）CM是弦吗？为什么？
（3）从图中你能找到哪些弦?巩固：●OBCA(1)如图,半径有:____________OA、OB、OC△AOB是_____三角形.(2)如图,弦有:______________AB、BC、AC 我们可以发现，在圆中有长度不等的弦，那么在一个圆中有没有最长的弦呢？等边等腰若∠AOB=60°，则 小明和小强为了探究⊙O中有没有最长的弦，经过了大量的测量，最后得出一致结论，直径是圆中最长的弦，你认为他们的结论对吗？试说说你的理由.探究： 特别地，圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆．·COAB 圆上任意两点间的部分叫做圆弧，简称弧．以A、B为端点的弧记作 ，读作“圆弧AB”或“弧AB”．弧·COAB劣弧与优弧 小于半圆的弧（如图 ）叫做劣弧; 大于半圆的弧（用三个字母表示，如图 ）叫做优弧.(1)如图,半圆有:___________(2)劣弧有：优弧有：巩固： 如图，请正确的方式表示出以点A为端点的优弧及劣弧. 在同圆或者等圆中，能够互相重合的弧叫做等弧。等弧1、判断正误(1)弦是直径；(2)半圆是弧；(5)圆心相同，半径相等的两个圆是同心圆;(6)半径相等的两个圆是等圆.(3)半圆是最长的弧；(4)直径是最长的弦；(7)相等的弧叫做等弧.2、如图：AB,CD为⊙O的直径，DE∥AB, ∠EOD=100°,求∠AOC的度数。3、如图：CD为⊙O直径，AE交⊙O于B，且AB=OC，∠A=200,求∠DOE的度数.变式：如图：AB为⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于点E，已知AB=2DE，∠AEC=200，求∠AOC的度数。AEDOCB4、如图：以O为圆心的同心圆，大圆的弦AB交小圆于C,D两点。求证:
(1)AC=BD;
(2)∠AOC=∠BOD.
E（1）圆的两个定义；
（2）同心圆、等圆；确定圆的条件；
（3）弦、弧（优弧、劣弧）；小结：