24.1.4 圆周角(2)
文档属性
| 名称 | 24.1.4 圆周角(2) |

|
|
| 格式 | rar | ||
| 文件大小 | 53.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-13 00:00:00 | ||
图片预览


文档简介
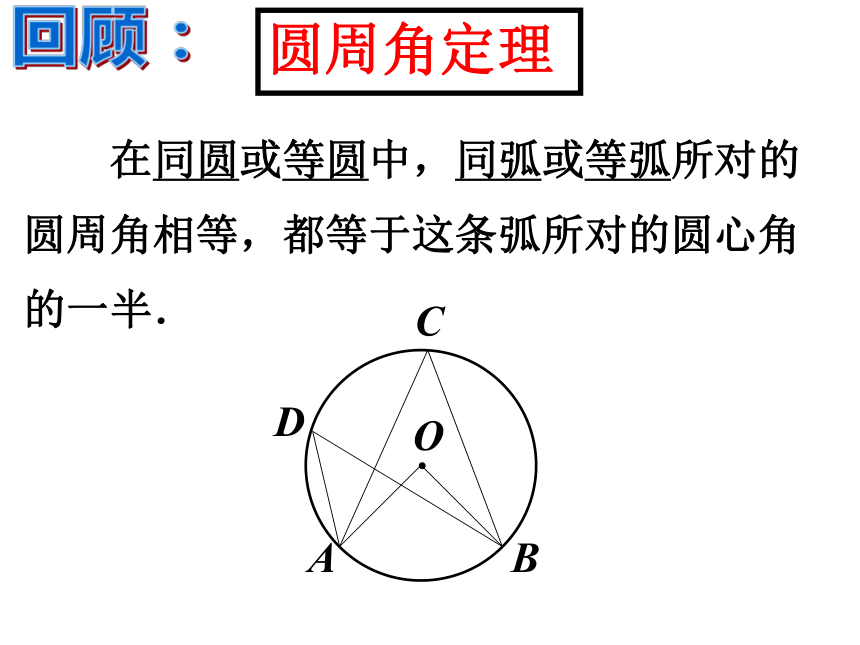
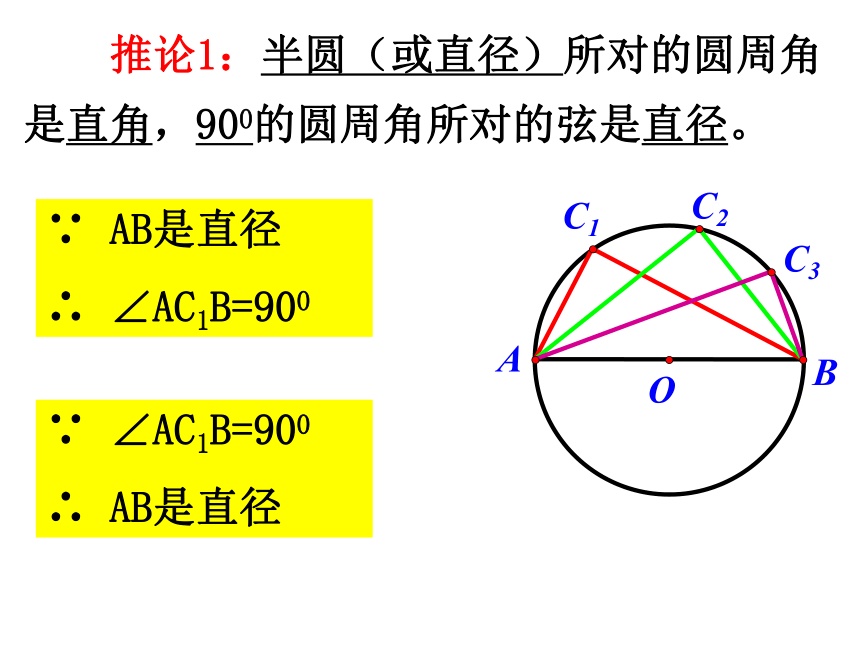
课件13张PPT。24.1.4 圆周角(2) 人教版九年级上册回顾: 在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.圆周角定理 推论1:半圆(或直径)所对的圆周角是直角,900的圆周角所对的弦是直径。∵ AB是直径
∴ ∠AC1B=900∵ ∠AC1B=900
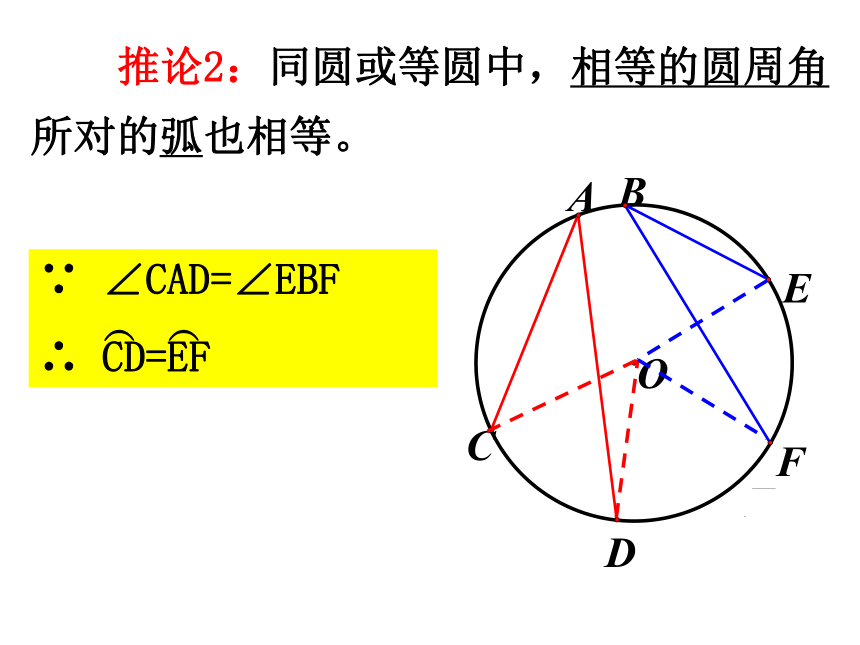
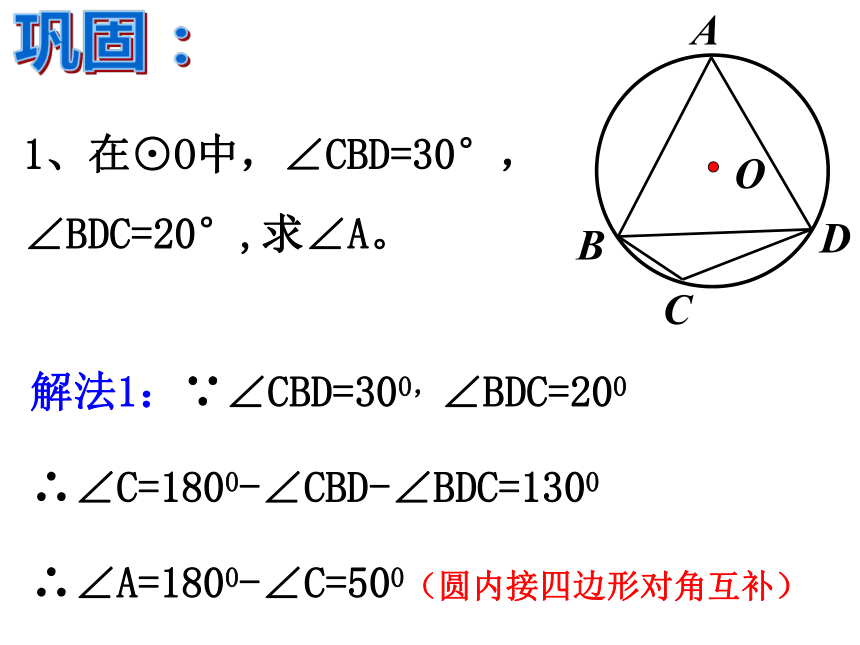
∴ AB是直径 推论2:同圆或等圆中,相等的圆周角所对的弧也相等。 特别提示:在同圆或等圆中,同弦或等弦所对的圆周角相等或互补。圆内接四边形的对角互补1、在⊙O中,∠CBD=30°,∠BDC=20°,求∠A。解法1:∵∠CBD=300,∠BDC=200
∴∠C=1800-∠CBD-∠BDC=1300
∴∠A=1800-∠C=500(圆内接四边形对角互补)巩固:1、在⊙O中,∠CBD=30°,∠BDC=20°,求∠A。解法2:连结AC,则
∠CAD=∠CBD=300
∠BAC=∠BDC=200
∴∠BAD=∠CAD+∠BAC=5001、在⊙O中,∠CBD=30°,∠BDC=20°,求∠A。解法3:变式:已知∠OAB等于40度,求∠C的度数. D2、如图,在⊙O中,AB为直径,CB=CF,
弦CG⊥AB,交AB于D,交BF于E。
求证:BE=EC))BE=EC∠EBC=∠ECBAB为直径CG⊥AB3、如图,BC为半圆O的直径,AB=AF,AC与BF交于点M。
(1)若∠FBC=α,求∠ACB(用α表示)
(2)过A作AD⊥BC于D,交BF于E,求证:BE=EM。))4、判断
(1)等弧所对的圆周角相等;
(2)相等的弧所对的圆周角也相等;
(3)900的角所对的弦是直径;
(4)同弦所对的圆周角相等。5、求证:如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。已知:如图,在△ABC中,点O是边AB的中点,且AB=2OC.求证:△ABC是Rt△.
∴ ∠AC1B=900∵ ∠AC1B=900
∴ AB是直径 推论2:同圆或等圆中,相等的圆周角所对的弧也相等。 特别提示:在同圆或等圆中,同弦或等弦所对的圆周角相等或互补。圆内接四边形的对角互补1、在⊙O中,∠CBD=30°,∠BDC=20°,求∠A。解法1:∵∠CBD=300,∠BDC=200
∴∠C=1800-∠CBD-∠BDC=1300
∴∠A=1800-∠C=500(圆内接四边形对角互补)巩固:1、在⊙O中,∠CBD=30°,∠BDC=20°,求∠A。解法2:连结AC,则
∠CAD=∠CBD=300
∠BAC=∠BDC=200
∴∠BAD=∠CAD+∠BAC=5001、在⊙O中,∠CBD=30°,∠BDC=20°,求∠A。解法3:变式:已知∠OAB等于40度,求∠C的度数. D2、如图,在⊙O中,AB为直径,CB=CF,
弦CG⊥AB,交AB于D,交BF于E。
求证:BE=EC))BE=EC∠EBC=∠ECBAB为直径CG⊥AB3、如图,BC为半圆O的直径,AB=AF,AC与BF交于点M。
(1)若∠FBC=α,求∠ACB(用α表示)
(2)过A作AD⊥BC于D,交BF于E,求证:BE=EM。))4、判断
(1)等弧所对的圆周角相等;
(2)相等的弧所对的圆周角也相等;
(3)900的角所对的弦是直径;
(4)同弦所对的圆周角相等。5、求证:如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。已知:如图,在△ABC中,点O是边AB的中点,且AB=2OC.求证:△ABC是Rt△.
同课章节目录
