24.2.1 点和圆的位置关系(1)
文档属性
| 名称 | 24.2.1 点和圆的位置关系(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 254.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-13 00:00:00 | ||
图片预览




文档简介
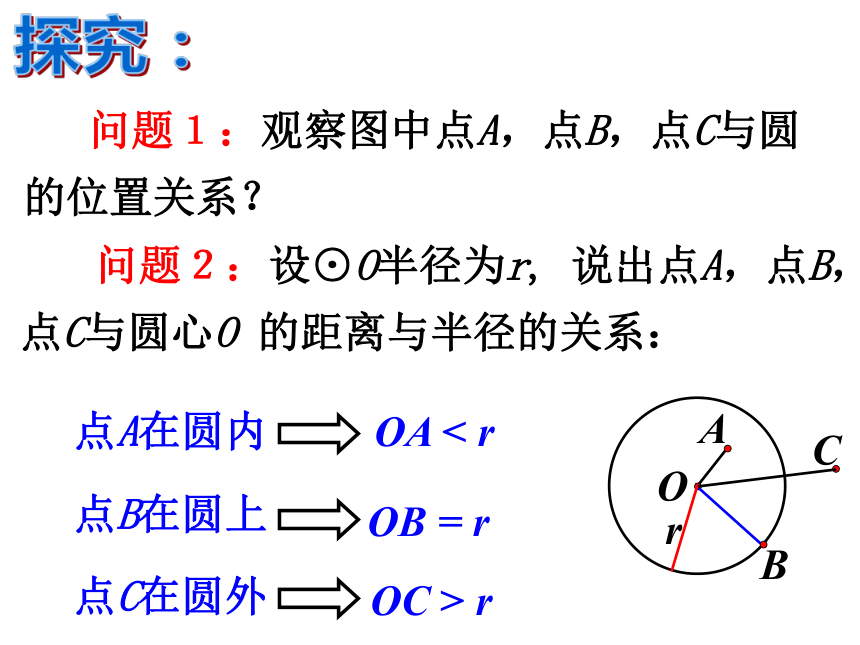
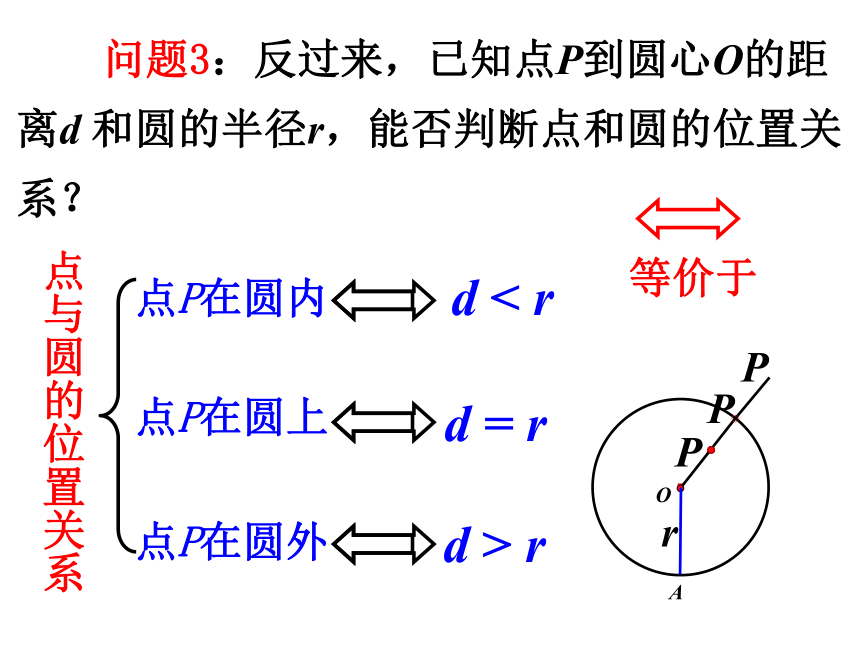
课件16张PPT。24.2.1 点和圆位置关系(1) 人教版九年级上册引入: 我国射击运动员在奥运会上屡获金牌,为我国赢得荣誉,右图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不等的圆)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?r 问题2:设⊙O半径为r, 说出点A,点B,点C与圆心O 的距离与半径的关系:·COABOC > r 问题1:观察图中点A,点B,点C与圆的位置关系?OA < rOB = r探究:点C在圆外点A在圆内点B在圆上r·OA 问题3:反过来,已知点P到圆心O的距离d 和圆的半径r,能否判断点和圆的位置关系?PPPd > rd < rd = r点P在圆外点P在圆内点P在圆上点与圆的位置关系1、已知⊙O的半径为10cm,点P到圆心O的距离为d,则
(1)当d=7cm时,点P在⊙O ;
(2)当d=10cm时,点P在⊙O ;
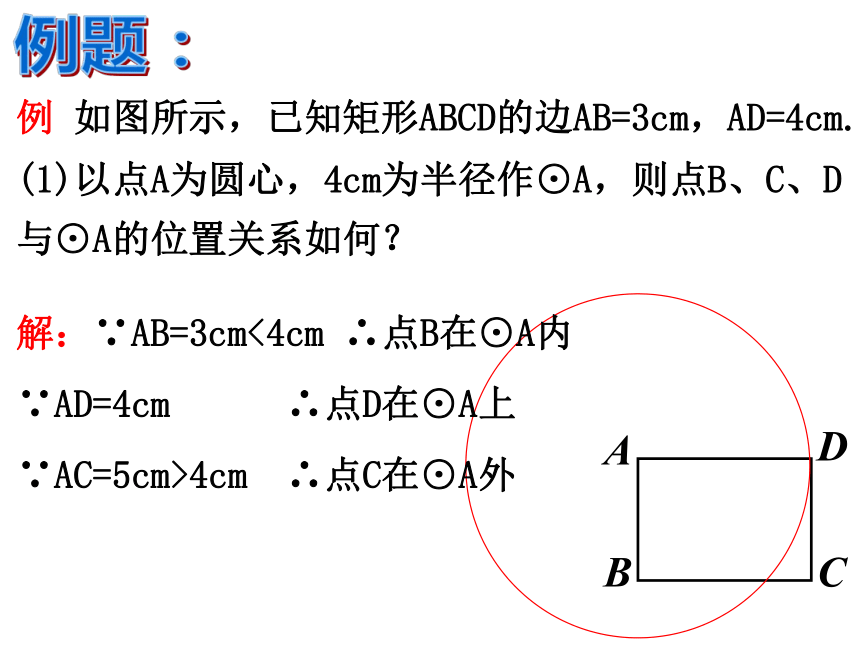
(3)当d=13cm时,点P在⊙O .巩固:内上外例 如图所示,已知矩形ABCD的边AB=3cm,AD=4cm.
(1)以点A为圆心,4cm为半径作⊙A,则点B、C、D与⊙A的位置关系如何?例题:解:∵AB=3cm<4cm ∴点B在⊙A内
∵AD=4cm ∴点D在⊙A上
∵AC=5cm>4cm ∴点C在⊙A外例 如图所示,已知矩形ABCD的边AB=3cm,AD=4cm.
(2)若以点A为圆心作⊙A,使B、C、D三点钟至少有一点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是什么?(2)连接AC
∵AB∴点B在⊙A内,点C在⊙A外
∵ABr
即 3cm
(1)当d=7cm时,点P在⊙O ;
(2)当d=10cm时,点P在⊙O ;
(3)当d=13cm时,点P在⊙O .巩固:内上外例 如图所示,已知矩形ABCD的边AB=3cm,AD=4cm.
(1)以点A为圆心,4cm为半径作⊙A,则点B、C、D与⊙A的位置关系如何?例题:解:∵AB=3cm<4cm ∴点B在⊙A内
∵AD=4cm ∴点D在⊙A上
∵AC=5cm>4cm ∴点C在⊙A外例 如图所示,已知矩形ABCD的边AB=3cm,AD=4cm.
(2)若以点A为圆心作⊙A,使B、C、D三点钟至少有一点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是什么?(2)连接AC
∵AB
∵AB
即 3cm
同课章节目录
