24.2.1 点和圆的位置关系(2)
文档属性
| 名称 | 24.2.1 点和圆的位置关系(2) |

|
|
| 格式 | rar | ||
| 文件大小 | 62.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-13 00:00:00 | ||
图片预览



文档简介
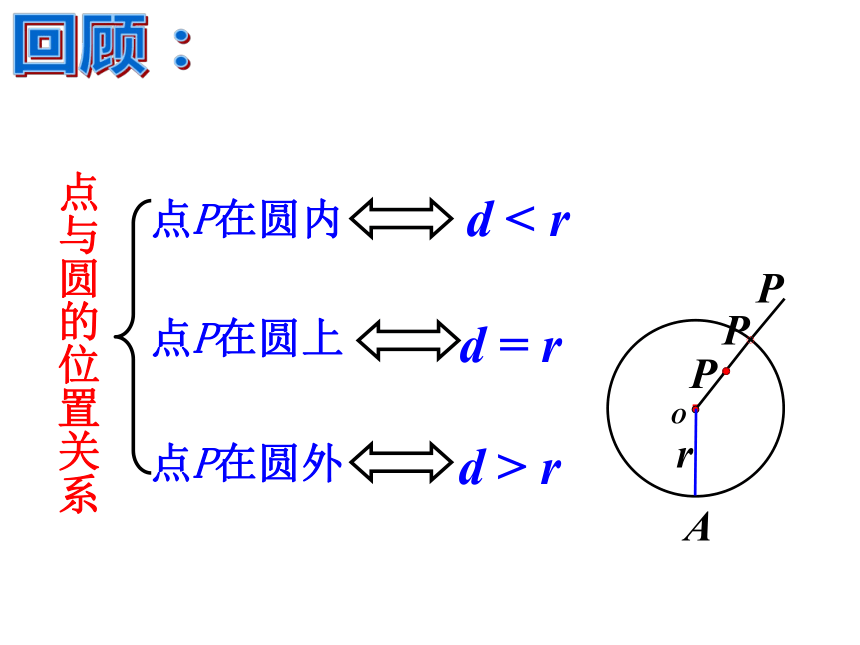
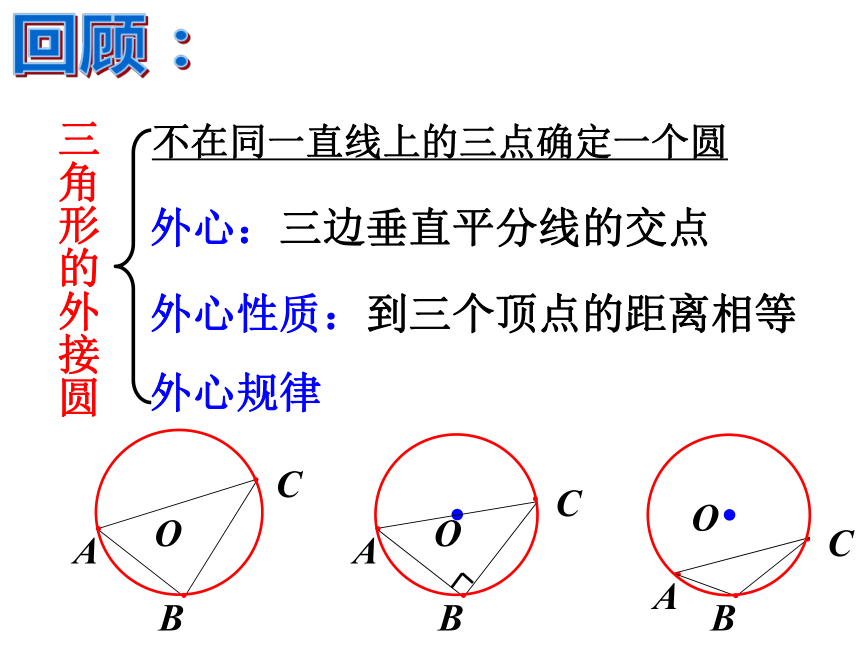
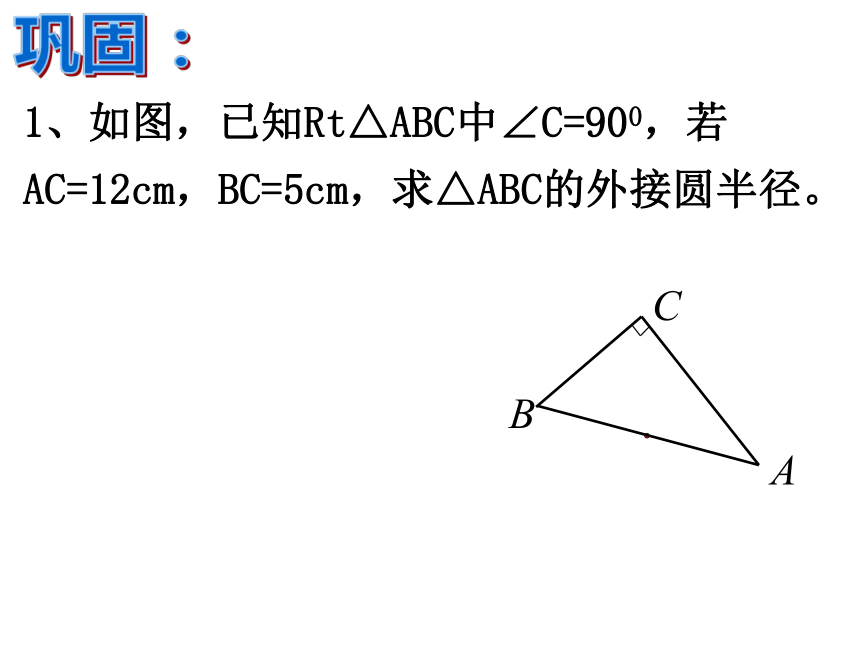
课件12张PPT。24.2.1 点和圆位置关系(2) 人教版九年级上册回顾:r·OAPPPd > rd < rd = r点P在圆外点P在圆内点P在圆上点与圆的位置关系回顾:外心规律外心:三边垂直平分线的交点外心性质:到三个顶点的距离相等三角形的外接圆不在同一直线上的三点确定一个圆例 如图,△ABC中,AB=AC=10,BC=12,求△ABC的外接圆半径。例题:解:过点A作AD⊥BC于D,由AB=AC知外接圆的圆心在AD上,记为O,故BD=1/2 BC=6,连接OB.设OA=OB=x.DO由BD2+OD2=OB2得,62+(8-x)2=x2解得即外接圆的半径为 .1、如图,已知Rt△ABC中∠C=900,若AC=12cm,BC=5cm,求△ABC的外接圆半径。 巩固:2、如图,已知等边三角形ABC中,边长为6cm,求它的外接圆半径。3、如图,AD是△ABC的外角∠EAC的平分线,AD与三角形的外接圆交于点D,连接BD,求证:DB=DC. 问题:经过同一条直线l上的三点能作出一个圆吗?探究: 如图,假设过同一直线l上的三点A、B、C能作出一个圆。 设这个圆的圆心为P,则点P在线段AB和线段BC的垂直平分线l1、l2上,即点P是l1、l2的交点,并且l1⊥l,l2⊥l,这与“过一点有且只有一条直线与已知直线垂直”矛盾。 所以,过同一直线上的三点不能作圆。ll1l2 归纳上面证明方法的步骤:
(1)假设命题的结论不成立;
(2)从这个假设出发,经过推理论证,得出矛盾;
(3)由矛盾断定假设不成立,从而得到原命题成立。归纳:反证法4、如图,已知AB、CD是⊙O的两条非直径弦,相交于点P.求证:AB与CD不能互相平分。巩固: 问题:任意四个点是不是可以作一个圆?请举例说明.思考:1. 四点在一条直线上不能作圆;3. 四点中任意三点不在一条直线可能作圆也可能作不出一个圆.2. 三点在同一直线上, 另一点不在这条直线上不能作圆;小结:
(1)假设命题的结论不成立;
(2)从这个假设出发,经过推理论证,得出矛盾;
(3)由矛盾断定假设不成立,从而得到原命题成立。归纳:反证法4、如图,已知AB、CD是⊙O的两条非直径弦,相交于点P.求证:AB与CD不能互相平分。巩固: 问题:任意四个点是不是可以作一个圆?请举例说明.思考:1. 四点在一条直线上不能作圆;3. 四点中任意三点不在一条直线可能作圆也可能作不出一个圆.2. 三点在同一直线上, 另一点不在这条直线上不能作圆;小结:
同课章节目录
