24.2.2 直线和圆的位置关系(1)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系(1) |  | |
| 格式 | rar | ||
| 文件大小 | 118.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-13 22:45:00 | ||
图片预览

文档简介
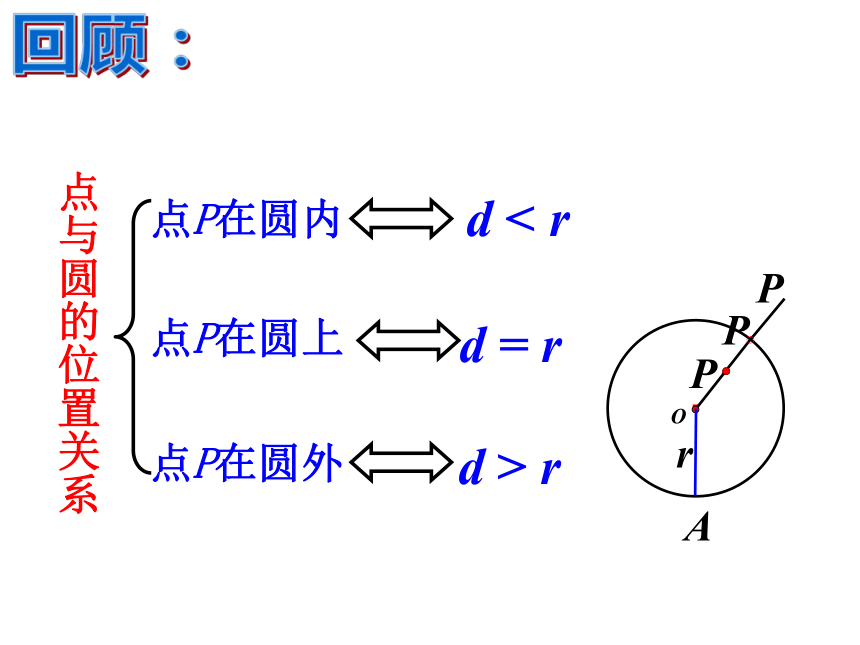
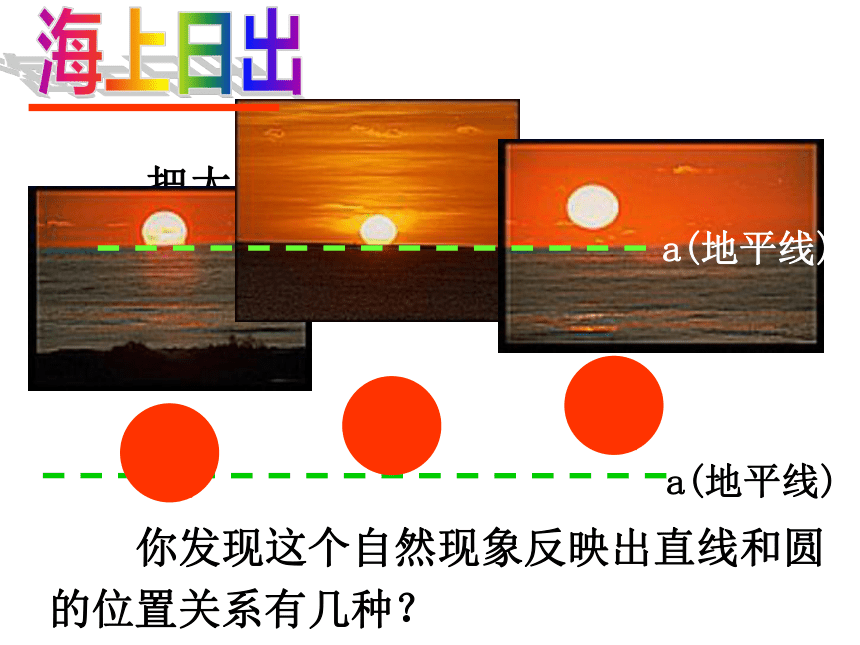
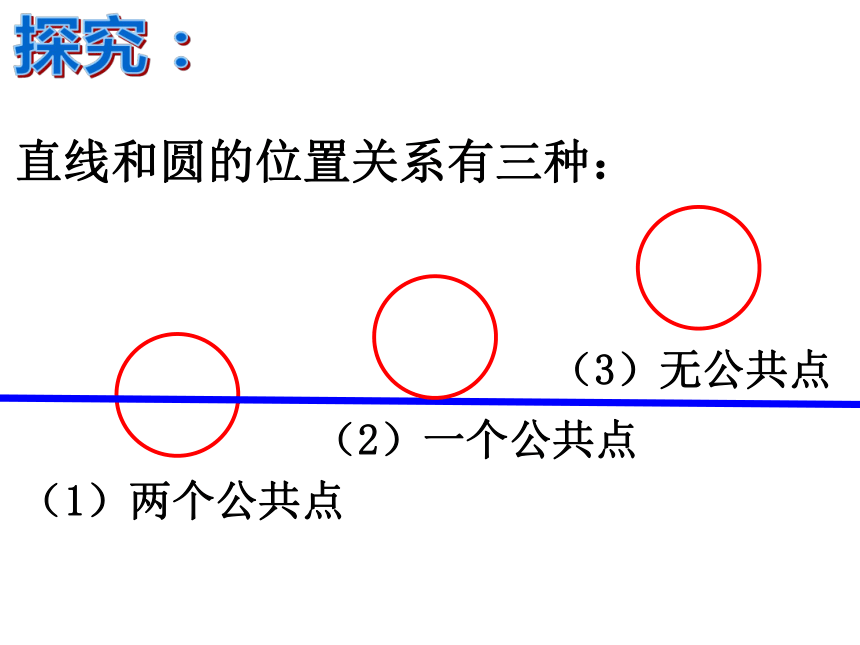
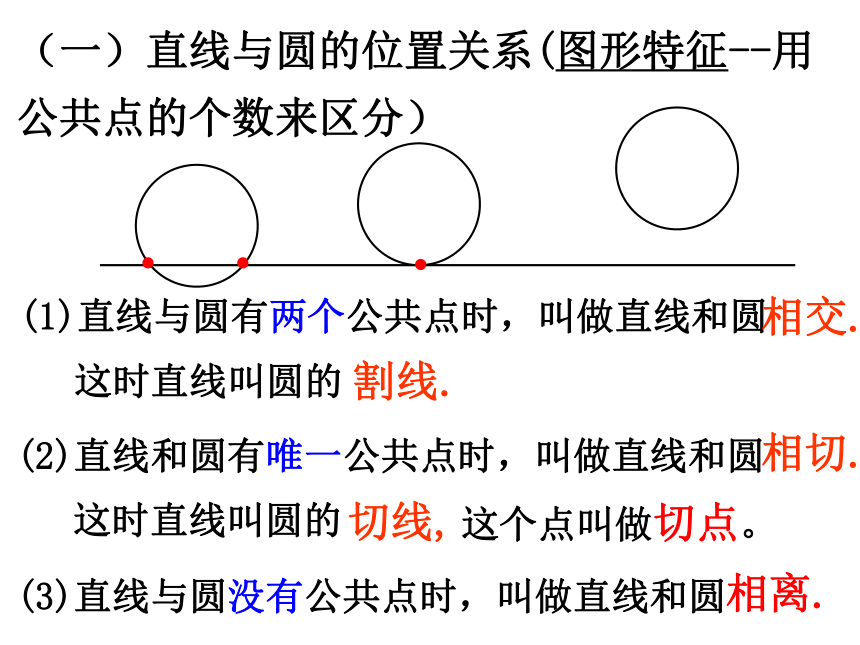
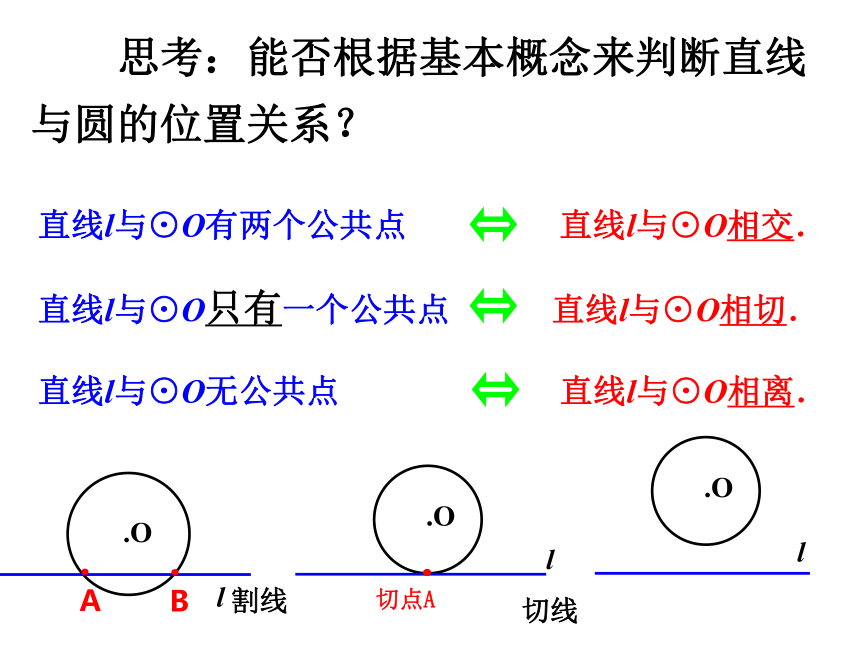
课件18张PPT。24.2.2 直线和圆位置关系 人教版九年级上册回顾:r·OAPPPd > rd < rd = r点P在圆外点P在圆内点P在圆上点与圆的位置关系 把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的位置关系。 你发现这个自然现象反映出直线和圆的位置关系有几种?海上日出a(地平线)直线和圆的位置关系有三种:(1)两个公共点(2)一个公共点(3)无公共点探究:(2)直线和圆有唯一公共点时,叫做直线和圆相切.(1)直线与圆有两个公共点时,叫做直线和圆 这时直线叫圆的割线.这时直线叫圆的切线,相交.(3)直线与圆没有公共点时,叫做直线和圆相离. (一)直线与圆的位置关系(图形特征--用公共点的个数来区分)这个点叫做切点。 思考:能否根据基本概念来判断直线与圆的位置关系?直线l与⊙O有两个公共点 直线l与⊙O相交.
直线l与⊙O只有一个公共点 直线l与⊙O相切.
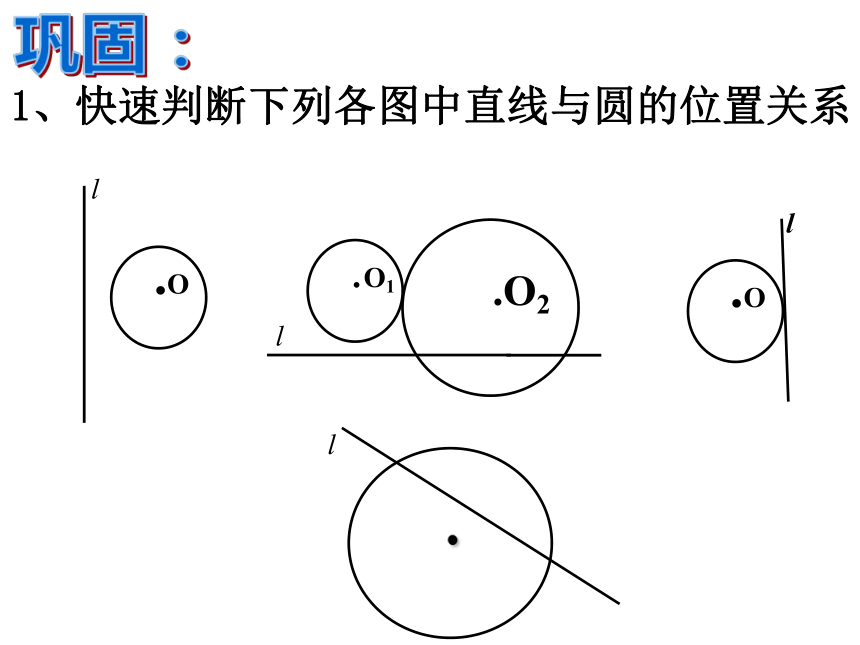
直线l与⊙O无公共点 直线l与⊙O相离.1、快速判断下列各图中直线与圆的位置关系ll.O2ll.巩固:(1)直线与圆最多有两个公共点. ( ) √×(3)若A是⊙O上一点,则直线AB与⊙O相切.( ).A.O(2)若直线与圆相交,则直线上的点都在圆内.( ) (4)若C为⊙O外的一点,则过点C的直线CD与⊙O相交或相离。( )××2、判断.CO 是否还有其他的方法判断直线与圆的位置关系? 设⊙O的半径为r,直线l到圆心O的距离为d,在直线和圆的不同位置关系中,d与r具有怎样的大小关系?
反过来,你能根据d与r的大小关系来确定直线和圆的位置关系吗? 探究:d>r 直线l与⊙O相离d=r 直线l与⊙O相切d r没有归纳: 例:在Rt△ABC中,∠C=900,AC=3cm,BC=4cm,以C为圆心,以R为半径的圆与AB 有怎样的位置关系?为什么?A应用:MBC 例:在Rt△ABC中,∠C=900,AC=3cm,BC=4cm,以C为圆心,以R为半径的圆与AB 有怎样的位置关系?为什么?A应用:MBC3.已知⊙O的半径为5cm,圆心O到直线a 的距离为3cm,则⊙O与直线a的位置关系是 .直线a与⊙O的公共点个数是 .
4.已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 .相交 相切两个巩固:
5.已知⊙O的半径为6cm,圆心O到直线a的距离为7cm,则直线a与⊙O的公共点个数是 .
6.已知⊙O的直径是6cm,圆心O到直线a的距离是4cm,则⊙O与直线a的位置关系是 .0相离7.设⊙O的半径为4,圆心O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d为( ).
A、d≤4 B、d<4 C、d≥4 D、d=48.设⊙P的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是( ).
A、相交 B、相切
C、相离 D、相切或相交CD 设⊙O的圆心O到直线的距离为d,半径为r,d,r是方程(m+9)x2-(m+6)x +1=0的两根,且直线与⊙O相切时,求m的值?方程 几何综合练习题d=r析:直线与⊙O相切b2-4ac=0[-(m+6)]2-4(m+9)=0解得 m1= -8 m2= 0当m=-8时原方程 为x2+2x+1=0x1=x2= -1当m=0时原方程 为9x2-6x+1=0(不符合题意舍去)2个交点割线1个切点切线d < rd = rd > r没有小结:
直线l与⊙O只有一个公共点 直线l与⊙O相切.
直线l与⊙O无公共点 直线l与⊙O相离.1、快速判断下列各图中直线与圆的位置关系ll.O2ll.巩固:(1)直线与圆最多有两个公共点. ( ) √×(3)若A是⊙O上一点,则直线AB与⊙O相切.( ).A.O(2)若直线与圆相交,则直线上的点都在圆内.( ) (4)若C为⊙O外的一点,则过点C的直线CD与⊙O相交或相离。( )××2、判断.CO 是否还有其他的方法判断直线与圆的位置关系? 设⊙O的半径为r,直线l到圆心O的距离为d,在直线和圆的不同位置关系中,d与r具有怎样的大小关系?
反过来,你能根据d与r的大小关系来确定直线和圆的位置关系吗? 探究:d>r 直线l与⊙O相离d=r 直线l与⊙O相切d
4.已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 .相交 相切两个巩固:
5.已知⊙O的半径为6cm,圆心O到直线a的距离为7cm,则直线a与⊙O的公共点个数是 .
6.已知⊙O的直径是6cm,圆心O到直线a的距离是4cm,则⊙O与直线a的位置关系是 .0相离7.设⊙O的半径为4,圆心O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d为( ).
A、d≤4 B、d<4 C、d≥4 D、d=48.设⊙P的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是( ).
A、相交 B、相切
C、相离 D、相切或相交CD 设⊙O的圆心O到直线的距离为d,半径为r,d,r是方程(m+9)x2-(m+6)x +1=0的两根,且直线与⊙O相切时,求m的值?方程 几何综合练习题d=r析:直线与⊙O相切b2-4ac=0[-(m+6)]2-4(m+9)=0解得 m1= -8 m2= 0当m=-8时原方程 为x2+2x+1=0x1=x2= -1当m=0时原方程 为9x2-6x+1=0(不符合题意舍去)2个交点割线1个切点切线d < rd = rd > r没有小结:
同课章节目录
