24.2.2 切线的性质定理
文档属性
| 名称 | 24.2.2 切线的性质定理 |

|
|
| 格式 | rar | ||
| 文件大小 | 139.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-13 00:00:00 | ||
图片预览


文档简介
课件16张PPT。24.2.2 切线的性质定理 人教版九年级上册判定一条直线是圆的切线的三种方法:
(1)根据切线定义判定.即与圆有唯一公共点的直线是圆的切线.
(2)根据圆心到直线的距离来判定,即与圆心的距离等于圆的半径的直线是圆的切线.(无交点,作垂直,证半径)
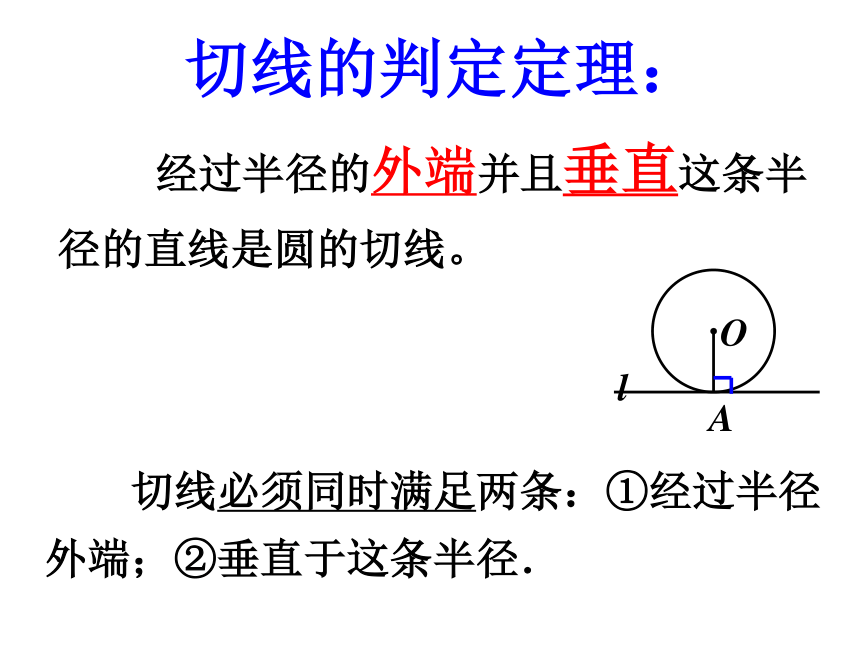
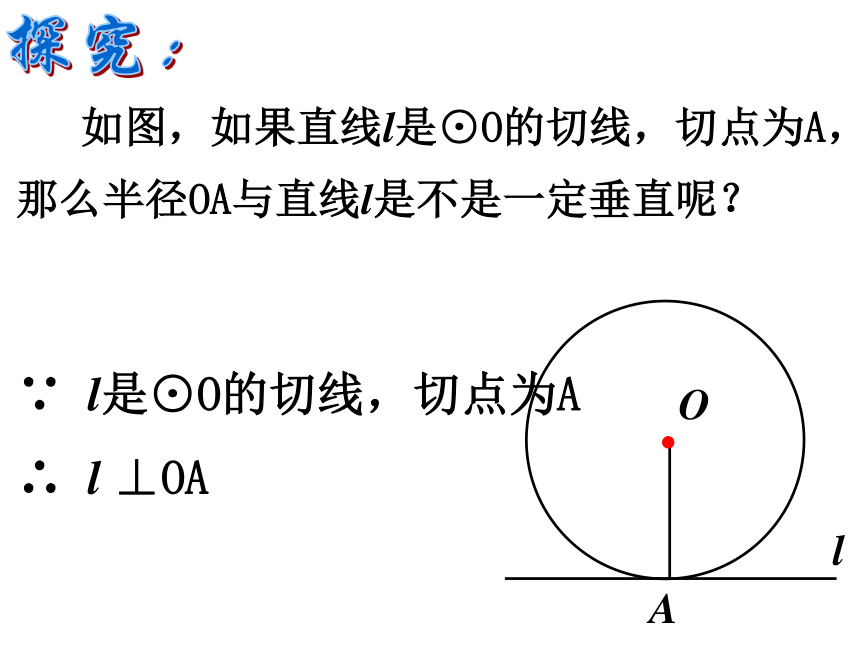
(3)根据切线的判定定理来判定.(有交点,作半径,证垂直)回顾:切线的判定定理: 经过半径的外端并且垂直这条半径的直线是圆的切线。 切线必须同时满足两条:①经过半径外端;②垂直于这条半径. 如图,如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢?探究:OAl∵ l是⊙O的切线,切点为A
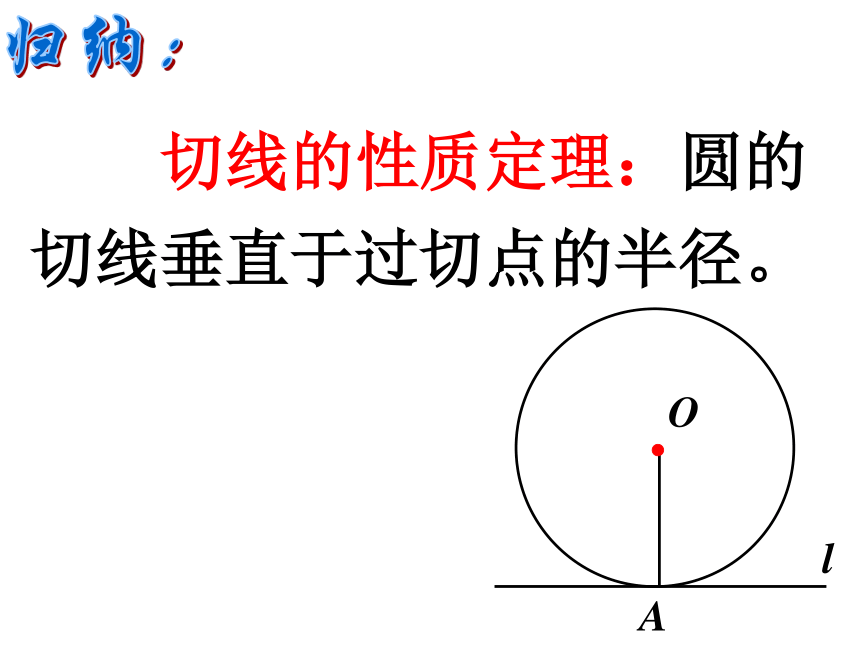
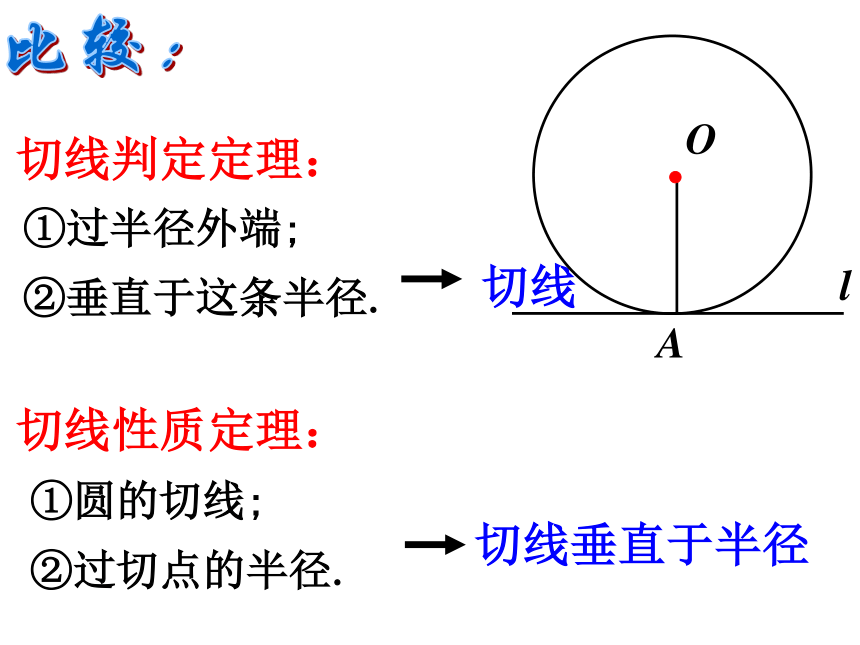
∴ l ⊥OA 切线的性质定理:圆的切线垂直于过切点的半径。归纳:①过半径外端;
②垂直于这条半径.切线①圆的切线;
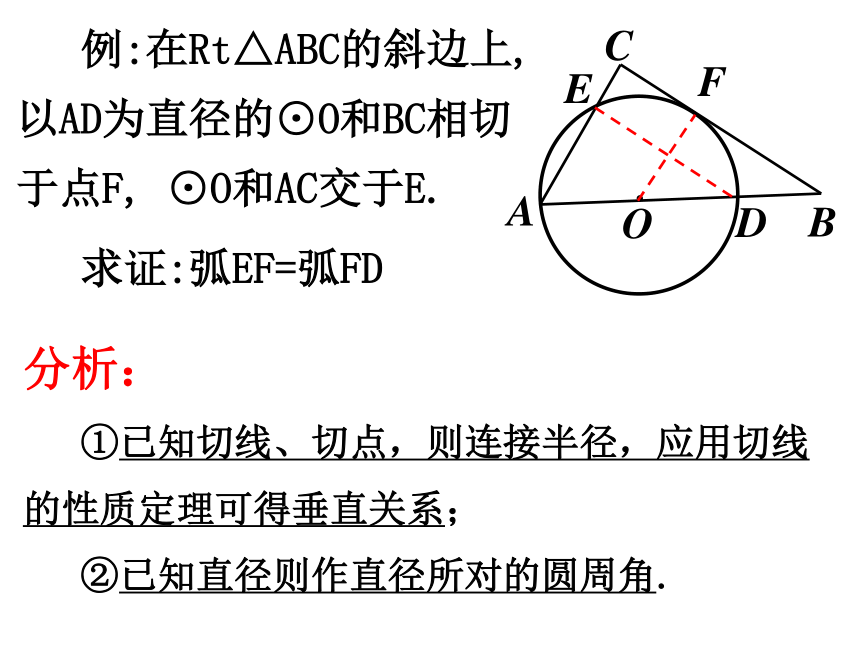
②过切点的半径.切线垂直于半径切线判定定理:切线性质定理:比较: 例:在Rt△ABC的斜边上,以AD为直径的⊙O和BC相切于点F, ⊙O和AC交于E.
求证:弧EF=弧FD分析:
①已知切线、切点,则连接半径,应用切线的性质定理可得垂直关系;
②已知直径则作直径所对的圆周角.1、如图, ⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少?巩固: 注:已知切线、切点,则连接半径,应用切线的性质定理得到垂直关系,从而应用勾股定理计算。2、如图,AB、AC分别切⊙O于B、C,若∠A=600,点P是圆上异于B、C的一动点,则∠BPC的度数是( ) A、600 B、1200 C、600或1200 D、1400或6003、如图,⊙O的直径AB=6cm,P是AB的延长线上一点,过点P作⊙O的切线,切点为C,连接AC.
(1)若∠CPA=300,求PC的长;
(2)若点P在AB的延长线上运动,∠CPA的平分线交AC于点M,∠CMP的大小是否发生变化?若变化,请说明理由;若不变,求出∠CMP的值.4、⊙O是△APC的外接圆,BD是⊙O的切线,切点为A,∠C=500,则∠PAD= .概念:
弦切角:切线与弦的夹角,如∠PAD。弦切角定理: 弦切角等于切线与弦所夹劣弧所对的圆周角。 ∵BD是⊙O的切线,切点为A
∴∠PAD=∠ACP(弦切角定理) 注:应用此定理时必须按照上述格式。5、如图,P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,弦AB与PO交于C,⊙O半径为1,PO=2,则PA=_______,PB=______,PC=_____,AC=______,BC=____,∠AOB=______.练习:已知,如图,D(0,1),⊙D交y轴于A、B两点,交x负半
轴于C点,过C点的直线:y=-2x-4与y轴交于P.
⑴试猜想PC与⊙D的位置关系,并说明理由.分析:做此类题,尤其强调
数形结合,同学们应把题中
数据“放入”图中。猜想直线
PC与⊙D相切。怎么证?联
想证明切线的两种方法。点
C在圆上,即证:∠DCP=90°
利用勾股及逆定理可得。切
线
判
定令x=0,得y=-4;令y=0,得x=-2
∴C(-2,0), P(0,-4)
又∵D(0,1) ∴OC=2, OP=4 ,OD=1, DP=5又∵在Rt△COD中, CD2=OC2+OD2=4+1=5
在Rt△COP中, CP2=OC2+OP2=4+16=20在△CPD中, CD2+CP2=5+20=25, DP2=25∴CD2+CP2=DP2
即:△CDP为直角三角形,且∠DCP=90°
∴PC为⊙D的切线.证明:∵直线y=-2x-4解: PC是⊙O的切线,勾股(逆)定理圆与一次函数拓展:已知,如图,D(0,1),⊙D交y轴于A、B两点,交x轴负
半轴于C点,过C点的直线:y=-2x-4与y轴交于P.
⑵判断在直线PC上是否存在点E,使得S△EOC=
4S△CDO,若存在,求出点E的坐标;若不存在,
请说明理由.
存
在
性
问
题解:假设在直线PC上存在这样的点E(x0,y0),使得S△EOC =4S △CDO,∵E点在直线PC:y=-2x-4上,∴当y0=4时有: 当y0=-4时有:∴在直线PC上存在满足条件的E点,其的坐标为(-4,4) , (0,-4) .抓住不变量
分类讨论
(1)根据切线定义判定.即与圆有唯一公共点的直线是圆的切线.
(2)根据圆心到直线的距离来判定,即与圆心的距离等于圆的半径的直线是圆的切线.(无交点,作垂直,证半径)
(3)根据切线的判定定理来判定.(有交点,作半径,证垂直)回顾:切线的判定定理: 经过半径的外端并且垂直这条半径的直线是圆的切线。 切线必须同时满足两条:①经过半径外端;②垂直于这条半径. 如图,如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢?探究:OAl∵ l是⊙O的切线,切点为A
∴ l ⊥OA 切线的性质定理:圆的切线垂直于过切点的半径。归纳:①过半径外端;
②垂直于这条半径.切线①圆的切线;
②过切点的半径.切线垂直于半径切线判定定理:切线性质定理:比较: 例:在Rt△ABC的斜边上,以AD为直径的⊙O和BC相切于点F, ⊙O和AC交于E.
求证:弧EF=弧FD分析:
①已知切线、切点,则连接半径,应用切线的性质定理可得垂直关系;
②已知直径则作直径所对的圆周角.1、如图, ⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少?巩固: 注:已知切线、切点,则连接半径,应用切线的性质定理得到垂直关系,从而应用勾股定理计算。2、如图,AB、AC分别切⊙O于B、C,若∠A=600,点P是圆上异于B、C的一动点,则∠BPC的度数是( ) A、600 B、1200 C、600或1200 D、1400或6003、如图,⊙O的直径AB=6cm,P是AB的延长线上一点,过点P作⊙O的切线,切点为C,连接AC.
(1)若∠CPA=300,求PC的长;
(2)若点P在AB的延长线上运动,∠CPA的平分线交AC于点M,∠CMP的大小是否发生变化?若变化,请说明理由;若不变,求出∠CMP的值.4、⊙O是△APC的外接圆,BD是⊙O的切线,切点为A,∠C=500,则∠PAD= .概念:
弦切角:切线与弦的夹角,如∠PAD。弦切角定理: 弦切角等于切线与弦所夹劣弧所对的圆周角。 ∵BD是⊙O的切线,切点为A
∴∠PAD=∠ACP(弦切角定理) 注:应用此定理时必须按照上述格式。5、如图,P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,弦AB与PO交于C,⊙O半径为1,PO=2,则PA=_______,PB=______,PC=_____,AC=______,BC=____,∠AOB=______.练习:已知,如图,D(0,1),⊙D交y轴于A、B两点,交x负半
轴于C点,过C点的直线:y=-2x-4与y轴交于P.
⑴试猜想PC与⊙D的位置关系,并说明理由.分析:做此类题,尤其强调
数形结合,同学们应把题中
数据“放入”图中。猜想直线
PC与⊙D相切。怎么证?联
想证明切线的两种方法。点
C在圆上,即证:∠DCP=90°
利用勾股及逆定理可得。切
线
判
定令x=0,得y=-4;令y=0,得x=-2
∴C(-2,0), P(0,-4)
又∵D(0,1) ∴OC=2, OP=4 ,OD=1, DP=5又∵在Rt△COD中, CD2=OC2+OD2=4+1=5
在Rt△COP中, CP2=OC2+OP2=4+16=20在△CPD中, CD2+CP2=5+20=25, DP2=25∴CD2+CP2=DP2
即:△CDP为直角三角形,且∠DCP=90°
∴PC为⊙D的切线.证明:∵直线y=-2x-4解: PC是⊙O的切线,勾股(逆)定理圆与一次函数拓展:已知,如图,D(0,1),⊙D交y轴于A、B两点,交x轴负
半轴于C点,过C点的直线:y=-2x-4与y轴交于P.
⑵判断在直线PC上是否存在点E,使得S△EOC=
4S△CDO,若存在,求出点E的坐标;若不存在,
请说明理由.
存
在
性
问
题解:假设在直线PC上存在这样的点E(x0,y0),使得S△EOC =4S △CDO,∵E点在直线PC:y=-2x-4上,∴当y0=4时有: 当y0=-4时有:∴在直线PC上存在满足条件的E点,其的坐标为(-4,4) , (0,-4) .抓住不变量
分类讨论
同课章节目录
