1.3.1 交集与并集 教案3
图片预览


文档简介
1.3.1
交集与并集
教案
教学分析
课本从学生熟悉的集合出发,结合实例,通过类比实数加法运算引入集合间的运算,同时,结合相关内容介绍子集和全集等概念.在安排这部分内容时,课本继续注重体现逻辑思考的方法,如归纳等.
值得注意的问题:在全集和补集的教学中,应注意利用图形的直观作用,帮助学生理解补集的概念,并能够用直观图进行求补集的运算.
三维目标
1.理解两个集合的并集与交集、全集的含义,掌握求两个简单集合的交集与并集的方法,会求给定子集的补集,感受集合作为一种语言,在表示数学内容时的简洁和准确,进一步提高类比的能力.
2.通过观察和类比,借助Venn图理解集合的基本运算.体会直观图示对理解抽象概念的作用,培养数形结合的思想.
重点难点
教学重点:交集与并集,全集与补集的概念.
教学难点:理解交集与并集的概念,以及符号之间的区别与联系.
课时安排
2课时
1.3.1 交集与并集
导入新课
思路1.我们知道,实数有加法运算,两个实数可以相加,例如5+3=8.类比实数的加法运算,集合是否也可以“相加”呢?教师直接点出课题.
思路2.请同学们考察下列各个集合,你能说出集合C与集合A,B之间的关系吗?
(1)A={1,3,5},B={2,4,6},C={1,2,3,4,5,6};
(2)A={x|x是有理数},B={x|x是无理数},C={x|x是实数}.
引导学生通过观察、类比、思考和交流,得出结论.教师强调集合也有运算,这就是我们本节课所要学习的内容.
思路3.(1)①如图1中甲和乙所示,观察两个图的阴影部分,它们分别同集合A、集合B有什么关系?
图1
②观察集合A,B与集合C={1,2,3,4}之间的关系.
学生思考交流并回答,教师直接指出这就是本节课学习的课题:集合的运算.
(2)①已知集合A={1,2,3},B={2,3,4},写出由集合A,B中的所有元素组成的集合C.
②已知集合A={x|x>1},B={x|x<0},在数轴上表示出集合A与B,并写出由集合A与B中的所有元素组成的集合C.
推进新课
①通过上述问题中集合A,B与集合C之间的关系,类比实数的加法运算,你发现了什么?
②用文字语言来叙述上述问题中集合A,B与集合C之间的关系.
③用数学符号来描述上述问题中,集合A,B与集合C之间的关系.
④试用Venn图表示A∪B=C.
⑤请给出集合并集的定义.
⑥求集合的并集是集合间的一种运算,那么,集合间还有其他运算吗?
请同学们观察下面的问题,集合A,B与集合C之间有什么关系?
A={2,4,6,8,10},B={3,5,8,12},C={8};
A={x|x是国兴中学2012年9月入学的高一年级女同学},B={x|x是国兴中学2012年9月入学的高一年级男同学},C={x|x是国兴中学2012年9月入学的高一年级同学}.
⑦类比集合的并集,请给出集合的交集定义,并分别用三种不同的语言形式来表达.
活动:先让学生思考或讨论问题,然后再回答,经教师提示、点拨,并对回答正确的学生及时表扬,对回答不准确的学生提示引导考虑问题的思路,主要引导学生发现集合的并集和交集运算,并能用数学符号来刻画,用Venn图来显示.
讨论结果:①集合之间也可以相加,也可以进行运算,但是为了不和实数的运算相混淆,规定这种运算不叫集合的加法,而是叫作求集合的并集.集合C叫集合A与B的并集,记为A∪B=C,读作A并B.
②所有属于集合A或属于集合B的元素组成了集合C.
③C={x|x∈A,或x∈B}.
④如图1所示.
⑤一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集.其含义用符号表示为A∪B={x|x∈A,或x∈B},用Venn图表示,如图1所示.
⑥集合之间还可以求它们的公共元素组成集合的运算,这种运算叫求集合的交集,记作A∩B,读作A交B.A∩B=C,A∪B=C.
⑦一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集.
其含义用符号表示为A∩B={x|x∈A,且x∈B},用Venn图表示,如图2所示.
图2
思路1
例1
某学校所有男生组成集合A,一年级的所有学生组成集合B,一年级的所有男生组成集合C,一年级的所有女生组成集合D.求A∩B,C∪D.
活动:让学生回顾集合的表示法和交集、并集的含义,由于本例题难度较小,让学生自己解决,重点是总结集合运算的方法.
解:A∩B={x|x是该校一年级的男生}=C;
C∪D={x|x是该校一年级学生}=B.
点评:本题主要考查集合的并集和交集.
变式训练
1.设集合A={x|x是不大于10的正奇数},B={x|x是12的正约数}.求A∩B,A∪B.
解:A={x|x是不大于10的正奇数}={1,3,5,7,9},
B={x|x是12的正约数}={1,2,3,4,6,12},
A∩B={1,3},A∪B={1,2,3,4,5,6,7,9,12}.
2.集合P={1,2,3,m},M={m2,3},P∪M={1,2,3,m},则m=________.
分析:由题意得m2=1或2或m,解得m=-1或1或或-或0.因m=1不合题意,故舍去.
答案:-1或或-或0
3.满足A∪B={0,2}的集合A与B的组数为( ).
A.2 B.5 C.7 D.9
分析:∵A∪B={0,2},∴A{0,2}.则A=或A={0}或A={2}或A={0,2}.当A=时,B={0,2};当A={0}时,则集合B={2}或{0,2};当A={2}时,则集合B={0}或{0,2};当A={0,2}时,则集合B=或{0}或{2}或{0,2},则满足条件的集合A与B的组数为1+2+2+4=9.
答案:D
4.设集合A={1,2},则满足A∪B={1,2,3}的集合B的个数是( ).
A.1
B.3
C.4
D.8
分析:转化为求集合A子集的个数.很明显3A,又A∪B={1,2,3},必有3∈B,即集合B中至少有一个元素3,其他元素来自集合A中,则集合B的个数等于A={1,2}的子集个数,又集合A中含有2个元素,则集合A有22=4个子集,所以满足条件的集合B共有4个.
答案:C
例2
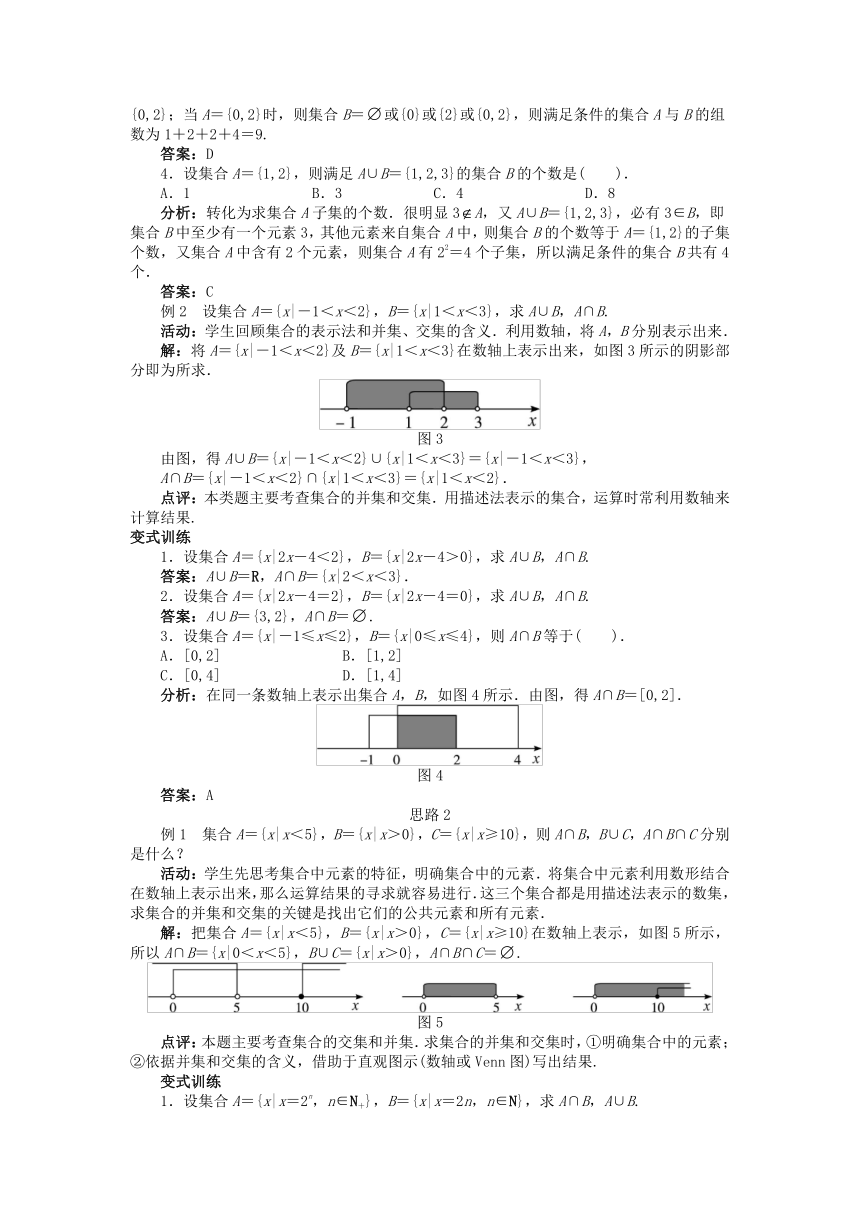
设集合A={x|-1<x<2},B={x|1<x<3},求A∪B,A∩B.
活动:学生回顾集合的表示法和并集、交集的含义.利用数轴,将A,B分别表示出来.
解:将A={x|-1<x<2}及B={x|1<x<3}在数轴上表示出来,如图3所示的阴影部分即为所求.
图3
由图,得A∪B={x|-1<x<2}∪{x|1<x<3}={x|-1<x<3},
A∩B={x|-1<x<2}∩{x|1<x<3}={x|1<x<2}.
点评:本类题主要考查集合的并集和交集.用描述法表示的集合,运算时常利用数轴来计算结果.
变式训练
1.设集合A={x|2x-4<2},B={x|2x-4>0},求A∪B,A∩B.
答案:A∪B=R,A∩B={x|2<x<3}.
2.设集合A={x|2x-4=2},B={x|2x-4=0},求A∪B,A∩B.
答案:A∪B={3,2},A∩B=.
3.设集合A={x|-1≤x≤2},B={x|0≤x≤4},则A∩B等于( ).
A.[0,2]
B.[1,2]
C.[0,4]
D.[1,4]
分析:在同一条数轴上表示出集合A,B,如图4所示.由图,得A∩B=[0,2].
图4
答案:A
思路2
例1
集合A={x|x<5},B={x|x>0},C={x|x≥10},则A∩B,B∪C,A∩B∩C分别是什么?
活动:学生先思考集合中元素的特征,明确集合中的元素.将集合中元素利用数形结合在数轴上表示出来,那么运算结果的寻求就容易进行.这三个集合都是用描述法表示的数集,求集合的并集和交集的关键是找出它们的公共元素和所有元素.
解:把集合A={x|x<5},B={x|x>0},C={x|x≥10}在数轴上表示,如图5所示,所以A∩B={x|0<x<5},B∪C={x|x>0},A∩B∩C=.
图5
点评:本题主要考查集合的交集和并集.求集合的并集和交集时,①明确集合中的元素;②依据并集和交集的含义,借助于直观图示(数轴或Venn图)写出结果.
变式训练
1.设集合A={x|x=2n,n∈N+},B={x|x=2n,n∈N},求A∩B,A∪B.
解:对任意m∈A,则有m=2n=2·2n-1,n∈N+,
因n∈N+,故n-1∈N,有2n-1∈N,
那么m∈B,即对任意m∈A有m∈B,
所以AB.
而10∈B但10A,
即AB,那么A∩B=A,A∪B=B.
2.设集合A={-4,2,a-1,a2},B={9,a-5,1-a},已知A∩B={9},求a.
解:因A∩B={9},
则9∈A,
则a-1=9或a2=9,a=10或a=±3.
当a=10时,a-5=5,1-a=-9,
则A={-4,2,9,100},B={9,5,-9}.
∴A∩B={9},
即a=10符合题意.
当a=3时,a-1=2不合题意;
当a=-3时,a-1=-4不合题意.
故a=10,此时A={-4,2,9,100},B={9,5,-9},满足A∩B={9}.
3.设集合A={x|2x+1<3},B={x|-3<x<2},则A∩B等于( ).
A.{x|-3<x<1}
B.{x|1<x<2}
C.{x|x>-3}
D.{x|x<1}
分析:集合A={x|2x+1<3}={x|x<1},观察或由数轴得A∩B={x|-3<x<1}.
答案:A
例2
设集合A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0,a∈R},若A∩B=B,求a的取值范围.
活动:明确集合A,B中的元素,教师和学生共同探讨满足A∩B=B的集合A,B的关系.集合A是方程x2+4x=0的解组成的集合,可以发现,BA,通过分类讨论集合B是否为空集来求a的值.利用集合的表示法来认识集合A,B均是方程的解集,通过画Venn图发现集合A,B的关系,从数轴上分析求得a的值.
解:由题意得A={-4,0}.
∵A∩B=B,
∴BA.
∴B=或B≠.
当B=时,即关于x的方程x2+2(a+1)x+a2-1=0无实数解,
则Δ=4(a+1)2-4(a2-1)<0,解得a<-1.
当B≠时,若集合B仅含有一个元素,
则Δ=4(a+1)2-4(a2-1)=0,解得a=-1,
此时,B={x|x2=0}={0}A,即a=-1符合题意.
若集合B含有两个元素,则这两个元素是-4,0,
即关于x的方程x2+2(a+1)x+a2-1=0的解是-4,0.
则有
解得a=1,则a=1符合题意.
综上所得,a=1或a≤-1.
变式训练
已知集合A={x|-2≤x≤5},集合B={x|m+1≤x≤2m-1},且A∪B=A,试求实数m的取值范围.
分析:由A∪B=A,得BA,则有B=或B≠,因此对集合B分类讨论.
解:∵A∪B=A,∴BA.
又∵A={x|-2≤x≤5}≠,∴B=,或B≠.
当B=时,有m+1>2m-1,∴m<2.
当B≠时,观察图6:
图6
由数轴可得解得2≤m≤3.
综上所述,实数m的取值范围是m<2或2≤m≤3,即m≤3.
点评:本题主要考查集合的运算、分类讨论的思想,以及集合间关系的应用.已知两个集合的运算结果,求集合中参数的值时,由集合的运算结果确定它们的关系,通过深刻理解集合表示法的转换,把相关问题化归为其他常见的方程、不等式等数学问题.这称为数学的化归思想,是数学中的常用方法,学会应用化归和分类讨论的数学思想方法解决有关问题.
1.设集合A={3,5,6,8},B={4,5,7,8},
(1)求A∩B,A∪0B;
(2)用适当的符号(或)填空:
A∩B________A,B________A∩B,A∪B________A,A∪B________B,A∩B________A∪B.
解:(1)因A,B的公共元素为5,8,故两集合的公共部分为5,8,
则A∩B={3,5,6,8}∩{4,5,7,8}={5,8}.
又A,B两集合的所有元素为3,4,5,6,7,8,
故A∪B={3,4,5,
6,7,8}.
(2)(A∩B)
A,B(A∩B),(A∪B)A,(A∪B)B,(A∩B)
(A∪B).
2.设集合A={x|x<5},B={x|x≥0},求A∩B.
解:因x<5及x≥0的公共部分为0≤x<5,
故A∩B={x|x<5}∩{x|x≥0}={x|0≤x<5}.
3.设集合A={x|x是锐角三角形},B={x|x是钝角三角形},求A∩B.
解:因三角形按角分类时,锐角三角形和钝角三角形彼此孤立,故A、B两集合没有公共部分.
所以A∩B={x|x是锐角三角形}∩{x|x是钝角三角形}=.
4.设集合A={x|x>-2},B={x|x≥3},求A∪B.
解:在数轴上将A,B分别表示出来,得A∪B={x|x>-2}.
5.设集合A={x|x是平行四边形},B={x|x是矩形},求A∪B.
解:因矩形是平行四边形,故由A,B的元素组成的集合为A∪B,A∪B={x|x是平行四边形}.
6.已知集合M={1},N={1,2},设A={(x,y)|x∈M,y∈N},B={(x,y)|x∈N,y∈M},求A∩B,A∪B.
分析:M,N中元素是数,A,B中元素是平面内点集,关键是找其元素.
解:∵M={1},N={1,2},则A={(1,1),(1,2)},B={(1,1),(2,1)},故A∩B={(1,1)},A∪B={(1,1),(1,2),(2,1)}.
7.若A,B,C为三个集合,A∪B=B∩C,则一定有( ).
A.AC B.CA C.A≠C D.A=
分析:思路一:∵(B∩C)B,(B∩C)C,A∪B=B∩C,
∴(A∪B)B,(A∪B)C.∴ABC.∴AC.
思路二:取满足条件的A={1},B={1,2},C={1,2,3},排除B,D,
令A={1,2},B={1,2},C={1,2},则此时也满足条件A∪B=B∩C,
而此时A=C,排除C.
答案:A
观察:(1)集合A={1,2},B={1,2,3,4}时,A∩B,A∪B这两个运算结果与集合A,B的关系;
(2)当A=时,A∩B,A∪B这两个运算结果与集合A,B的关系;
(3)当A=B={1,2}时,A∩B,A∪B这两个运算结果与集合A,B的关系.
由(1)(2)(3)你发现了什么结论?
活动:依据集合的交集和并集的含义写出运算结果,并观察与集合A,B的关系.用Venn图来发现运算结果与集合A,B的关系.(1)(2)(3)中的集合A,B均满足AB,用Venn图表示,就可以发现A∩B,A∪B与集合A,B的关系.
解:A∩B=AABA∪B=B.
可用类似方法得到集合的运算性质,归纳如下:
A∪B=B∪A,A(A∪B),B(A∪B);A∪A=A,A∪=A,ABA∪B=B;
A∩B=B∩A;(A∩B)A,(A∩B)B;A∩A=A;A∩=;ABA∩B=A.
本节主要学习了:
1.集合的交集和并集.
2.通常借助于数轴或Venn图来求交集和并集.
1.课外思考:对于集合的基本运算,你能得出哪些运算规律?
2.请你举出现实生活中的一个实例,并说明其并集、交集和补集的现实含义.
3.习题1—3 A组3,4.
由于本节课内容比较容易接受,也是历年高考的必考内容之一,所以在教学设计上注重加强练习和拓展课本内容.设计中通过借助数轴或Venn图写出集合运算的结果,这是突破本节教学难点的有效方法.
交集与并集
教案
教学分析
课本从学生熟悉的集合出发,结合实例,通过类比实数加法运算引入集合间的运算,同时,结合相关内容介绍子集和全集等概念.在安排这部分内容时,课本继续注重体现逻辑思考的方法,如归纳等.
值得注意的问题:在全集和补集的教学中,应注意利用图形的直观作用,帮助学生理解补集的概念,并能够用直观图进行求补集的运算.
三维目标
1.理解两个集合的并集与交集、全集的含义,掌握求两个简单集合的交集与并集的方法,会求给定子集的补集,感受集合作为一种语言,在表示数学内容时的简洁和准确,进一步提高类比的能力.
2.通过观察和类比,借助Venn图理解集合的基本运算.体会直观图示对理解抽象概念的作用,培养数形结合的思想.
重点难点
教学重点:交集与并集,全集与补集的概念.
教学难点:理解交集与并集的概念,以及符号之间的区别与联系.
课时安排
2课时
1.3.1 交集与并集
导入新课
思路1.我们知道,实数有加法运算,两个实数可以相加,例如5+3=8.类比实数的加法运算,集合是否也可以“相加”呢?教师直接点出课题.
思路2.请同学们考察下列各个集合,你能说出集合C与集合A,B之间的关系吗?
(1)A={1,3,5},B={2,4,6},C={1,2,3,4,5,6};
(2)A={x|x是有理数},B={x|x是无理数},C={x|x是实数}.
引导学生通过观察、类比、思考和交流,得出结论.教师强调集合也有运算,这就是我们本节课所要学习的内容.
思路3.(1)①如图1中甲和乙所示,观察两个图的阴影部分,它们分别同集合A、集合B有什么关系?
图1
②观察集合A,B与集合C={1,2,3,4}之间的关系.
学生思考交流并回答,教师直接指出这就是本节课学习的课题:集合的运算.
(2)①已知集合A={1,2,3},B={2,3,4},写出由集合A,B中的所有元素组成的集合C.
②已知集合A={x|x>1},B={x|x<0},在数轴上表示出集合A与B,并写出由集合A与B中的所有元素组成的集合C.
推进新课
①通过上述问题中集合A,B与集合C之间的关系,类比实数的加法运算,你发现了什么?
②用文字语言来叙述上述问题中集合A,B与集合C之间的关系.
③用数学符号来描述上述问题中,集合A,B与集合C之间的关系.
④试用Venn图表示A∪B=C.
⑤请给出集合并集的定义.
⑥求集合的并集是集合间的一种运算,那么,集合间还有其他运算吗?
请同学们观察下面的问题,集合A,B与集合C之间有什么关系?
A={2,4,6,8,10},B={3,5,8,12},C={8};
A={x|x是国兴中学2012年9月入学的高一年级女同学},B={x|x是国兴中学2012年9月入学的高一年级男同学},C={x|x是国兴中学2012年9月入学的高一年级同学}.
⑦类比集合的并集,请给出集合的交集定义,并分别用三种不同的语言形式来表达.
活动:先让学生思考或讨论问题,然后再回答,经教师提示、点拨,并对回答正确的学生及时表扬,对回答不准确的学生提示引导考虑问题的思路,主要引导学生发现集合的并集和交集运算,并能用数学符号来刻画,用Venn图来显示.
讨论结果:①集合之间也可以相加,也可以进行运算,但是为了不和实数的运算相混淆,规定这种运算不叫集合的加法,而是叫作求集合的并集.集合C叫集合A与B的并集,记为A∪B=C,读作A并B.
②所有属于集合A或属于集合B的元素组成了集合C.
③C={x|x∈A,或x∈B}.
④如图1所示.
⑤一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集.其含义用符号表示为A∪B={x|x∈A,或x∈B},用Venn图表示,如图1所示.
⑥集合之间还可以求它们的公共元素组成集合的运算,这种运算叫求集合的交集,记作A∩B,读作A交B.A∩B=C,A∪B=C.
⑦一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集.
其含义用符号表示为A∩B={x|x∈A,且x∈B},用Venn图表示,如图2所示.
图2
思路1
例1
某学校所有男生组成集合A,一年级的所有学生组成集合B,一年级的所有男生组成集合C,一年级的所有女生组成集合D.求A∩B,C∪D.
活动:让学生回顾集合的表示法和交集、并集的含义,由于本例题难度较小,让学生自己解决,重点是总结集合运算的方法.
解:A∩B={x|x是该校一年级的男生}=C;
C∪D={x|x是该校一年级学生}=B.
点评:本题主要考查集合的并集和交集.
变式训练
1.设集合A={x|x是不大于10的正奇数},B={x|x是12的正约数}.求A∩B,A∪B.
解:A={x|x是不大于10的正奇数}={1,3,5,7,9},
B={x|x是12的正约数}={1,2,3,4,6,12},
A∩B={1,3},A∪B={1,2,3,4,5,6,7,9,12}.
2.集合P={1,2,3,m},M={m2,3},P∪M={1,2,3,m},则m=________.
分析:由题意得m2=1或2或m,解得m=-1或1或或-或0.因m=1不合题意,故舍去.
答案:-1或或-或0
3.满足A∪B={0,2}的集合A与B的组数为( ).
A.2 B.5 C.7 D.9
分析:∵A∪B={0,2},∴A{0,2}.则A=或A={0}或A={2}或A={0,2}.当A=时,B={0,2};当A={0}时,则集合B={2}或{0,2};当A={2}时,则集合B={0}或{0,2};当A={0,2}时,则集合B=或{0}或{2}或{0,2},则满足条件的集合A与B的组数为1+2+2+4=9.
答案:D
4.设集合A={1,2},则满足A∪B={1,2,3}的集合B的个数是( ).
A.1
B.3
C.4
D.8
分析:转化为求集合A子集的个数.很明显3A,又A∪B={1,2,3},必有3∈B,即集合B中至少有一个元素3,其他元素来自集合A中,则集合B的个数等于A={1,2}的子集个数,又集合A中含有2个元素,则集合A有22=4个子集,所以满足条件的集合B共有4个.
答案:C
例2
设集合A={x|-1<x<2},B={x|1<x<3},求A∪B,A∩B.
活动:学生回顾集合的表示法和并集、交集的含义.利用数轴,将A,B分别表示出来.
解:将A={x|-1<x<2}及B={x|1<x<3}在数轴上表示出来,如图3所示的阴影部分即为所求.
图3
由图,得A∪B={x|-1<x<2}∪{x|1<x<3}={x|-1<x<3},
A∩B={x|-1<x<2}∩{x|1<x<3}={x|1<x<2}.
点评:本类题主要考查集合的并集和交集.用描述法表示的集合,运算时常利用数轴来计算结果.
变式训练
1.设集合A={x|2x-4<2},B={x|2x-4>0},求A∪B,A∩B.
答案:A∪B=R,A∩B={x|2<x<3}.
2.设集合A={x|2x-4=2},B={x|2x-4=0},求A∪B,A∩B.
答案:A∪B={3,2},A∩B=.
3.设集合A={x|-1≤x≤2},B={x|0≤x≤4},则A∩B等于( ).
A.[0,2]
B.[1,2]
C.[0,4]
D.[1,4]
分析:在同一条数轴上表示出集合A,B,如图4所示.由图,得A∩B=[0,2].
图4
答案:A
思路2
例1
集合A={x|x<5},B={x|x>0},C={x|x≥10},则A∩B,B∪C,A∩B∩C分别是什么?
活动:学生先思考集合中元素的特征,明确集合中的元素.将集合中元素利用数形结合在数轴上表示出来,那么运算结果的寻求就容易进行.这三个集合都是用描述法表示的数集,求集合的并集和交集的关键是找出它们的公共元素和所有元素.
解:把集合A={x|x<5},B={x|x>0},C={x|x≥10}在数轴上表示,如图5所示,所以A∩B={x|0<x<5},B∪C={x|x>0},A∩B∩C=.
图5
点评:本题主要考查集合的交集和并集.求集合的并集和交集时,①明确集合中的元素;②依据并集和交集的含义,借助于直观图示(数轴或Venn图)写出结果.
变式训练
1.设集合A={x|x=2n,n∈N+},B={x|x=2n,n∈N},求A∩B,A∪B.
解:对任意m∈A,则有m=2n=2·2n-1,n∈N+,
因n∈N+,故n-1∈N,有2n-1∈N,
那么m∈B,即对任意m∈A有m∈B,
所以AB.
而10∈B但10A,
即AB,那么A∩B=A,A∪B=B.
2.设集合A={-4,2,a-1,a2},B={9,a-5,1-a},已知A∩B={9},求a.
解:因A∩B={9},
则9∈A,
则a-1=9或a2=9,a=10或a=±3.
当a=10时,a-5=5,1-a=-9,
则A={-4,2,9,100},B={9,5,-9}.
∴A∩B={9},
即a=10符合题意.
当a=3时,a-1=2不合题意;
当a=-3时,a-1=-4不合题意.
故a=10,此时A={-4,2,9,100},B={9,5,-9},满足A∩B={9}.
3.设集合A={x|2x+1<3},B={x|-3<x<2},则A∩B等于( ).
A.{x|-3<x<1}
B.{x|1<x<2}
C.{x|x>-3}
D.{x|x<1}
分析:集合A={x|2x+1<3}={x|x<1},观察或由数轴得A∩B={x|-3<x<1}.
答案:A
例2
设集合A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0,a∈R},若A∩B=B,求a的取值范围.
活动:明确集合A,B中的元素,教师和学生共同探讨满足A∩B=B的集合A,B的关系.集合A是方程x2+4x=0的解组成的集合,可以发现,BA,通过分类讨论集合B是否为空集来求a的值.利用集合的表示法来认识集合A,B均是方程的解集,通过画Venn图发现集合A,B的关系,从数轴上分析求得a的值.
解:由题意得A={-4,0}.
∵A∩B=B,
∴BA.
∴B=或B≠.
当B=时,即关于x的方程x2+2(a+1)x+a2-1=0无实数解,
则Δ=4(a+1)2-4(a2-1)<0,解得a<-1.
当B≠时,若集合B仅含有一个元素,
则Δ=4(a+1)2-4(a2-1)=0,解得a=-1,
此时,B={x|x2=0}={0}A,即a=-1符合题意.
若集合B含有两个元素,则这两个元素是-4,0,
即关于x的方程x2+2(a+1)x+a2-1=0的解是-4,0.
则有
解得a=1,则a=1符合题意.
综上所得,a=1或a≤-1.
变式训练
已知集合A={x|-2≤x≤5},集合B={x|m+1≤x≤2m-1},且A∪B=A,试求实数m的取值范围.
分析:由A∪B=A,得BA,则有B=或B≠,因此对集合B分类讨论.
解:∵A∪B=A,∴BA.
又∵A={x|-2≤x≤5}≠,∴B=,或B≠.
当B=时,有m+1>2m-1,∴m<2.
当B≠时,观察图6:
图6
由数轴可得解得2≤m≤3.
综上所述,实数m的取值范围是m<2或2≤m≤3,即m≤3.
点评:本题主要考查集合的运算、分类讨论的思想,以及集合间关系的应用.已知两个集合的运算结果,求集合中参数的值时,由集合的运算结果确定它们的关系,通过深刻理解集合表示法的转换,把相关问题化归为其他常见的方程、不等式等数学问题.这称为数学的化归思想,是数学中的常用方法,学会应用化归和分类讨论的数学思想方法解决有关问题.
1.设集合A={3,5,6,8},B={4,5,7,8},
(1)求A∩B,A∪0B;
(2)用适当的符号(或)填空:
A∩B________A,B________A∩B,A∪B________A,A∪B________B,A∩B________A∪B.
解:(1)因A,B的公共元素为5,8,故两集合的公共部分为5,8,
则A∩B={3,5,6,8}∩{4,5,7,8}={5,8}.
又A,B两集合的所有元素为3,4,5,6,7,8,
故A∪B={3,4,5,
6,7,8}.
(2)(A∩B)
A,B(A∩B),(A∪B)A,(A∪B)B,(A∩B)
(A∪B).
2.设集合A={x|x<5},B={x|x≥0},求A∩B.
解:因x<5及x≥0的公共部分为0≤x<5,
故A∩B={x|x<5}∩{x|x≥0}={x|0≤x<5}.
3.设集合A={x|x是锐角三角形},B={x|x是钝角三角形},求A∩B.
解:因三角形按角分类时,锐角三角形和钝角三角形彼此孤立,故A、B两集合没有公共部分.
所以A∩B={x|x是锐角三角形}∩{x|x是钝角三角形}=.
4.设集合A={x|x>-2},B={x|x≥3},求A∪B.
解:在数轴上将A,B分别表示出来,得A∪B={x|x>-2}.
5.设集合A={x|x是平行四边形},B={x|x是矩形},求A∪B.
解:因矩形是平行四边形,故由A,B的元素组成的集合为A∪B,A∪B={x|x是平行四边形}.
6.已知集合M={1},N={1,2},设A={(x,y)|x∈M,y∈N},B={(x,y)|x∈N,y∈M},求A∩B,A∪B.
分析:M,N中元素是数,A,B中元素是平面内点集,关键是找其元素.
解:∵M={1},N={1,2},则A={(1,1),(1,2)},B={(1,1),(2,1)},故A∩B={(1,1)},A∪B={(1,1),(1,2),(2,1)}.
7.若A,B,C为三个集合,A∪B=B∩C,则一定有( ).
A.AC B.CA C.A≠C D.A=
分析:思路一:∵(B∩C)B,(B∩C)C,A∪B=B∩C,
∴(A∪B)B,(A∪B)C.∴ABC.∴AC.
思路二:取满足条件的A={1},B={1,2},C={1,2,3},排除B,D,
令A={1,2},B={1,2},C={1,2},则此时也满足条件A∪B=B∩C,
而此时A=C,排除C.
答案:A
观察:(1)集合A={1,2},B={1,2,3,4}时,A∩B,A∪B这两个运算结果与集合A,B的关系;
(2)当A=时,A∩B,A∪B这两个运算结果与集合A,B的关系;
(3)当A=B={1,2}时,A∩B,A∪B这两个运算结果与集合A,B的关系.
由(1)(2)(3)你发现了什么结论?
活动:依据集合的交集和并集的含义写出运算结果,并观察与集合A,B的关系.用Venn图来发现运算结果与集合A,B的关系.(1)(2)(3)中的集合A,B均满足AB,用Venn图表示,就可以发现A∩B,A∪B与集合A,B的关系.
解:A∩B=AABA∪B=B.
可用类似方法得到集合的运算性质,归纳如下:
A∪B=B∪A,A(A∪B),B(A∪B);A∪A=A,A∪=A,ABA∪B=B;
A∩B=B∩A;(A∩B)A,(A∩B)B;A∩A=A;A∩=;ABA∩B=A.
本节主要学习了:
1.集合的交集和并集.
2.通常借助于数轴或Venn图来求交集和并集.
1.课外思考:对于集合的基本运算,你能得出哪些运算规律?
2.请你举出现实生活中的一个实例,并说明其并集、交集和补集的现实含义.
3.习题1—3 A组3,4.
由于本节课内容比较容易接受,也是历年高考的必考内容之一,所以在教学设计上注重加强练习和拓展课本内容.设计中通过借助数轴或Venn图写出集合运算的结果,这是突破本节教学难点的有效方法.
