1.1.1 集合的概念 课件5
图片预览


文档简介
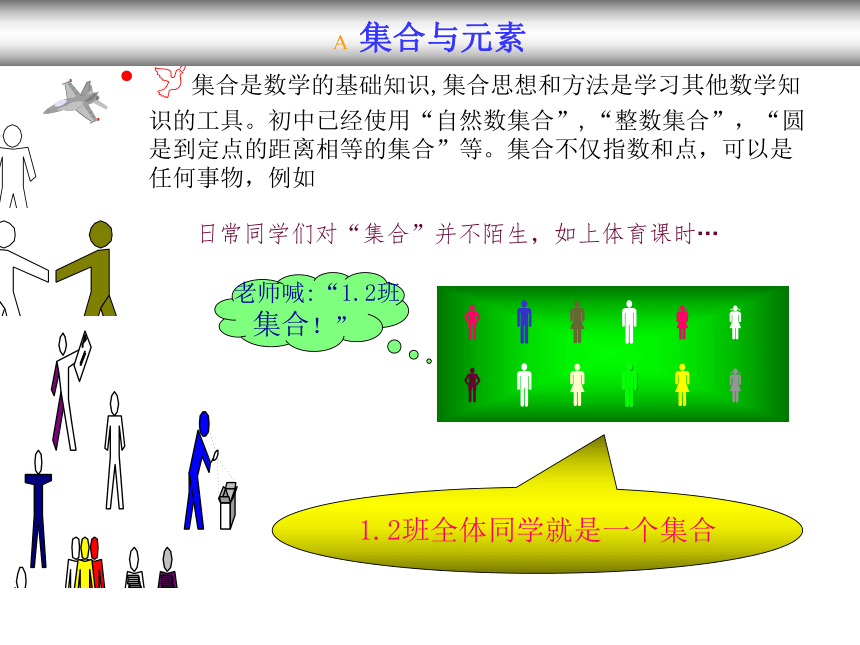
课件14张PPT。? 集合与元素 集合的概念集合的概念??集合是数学的基础知识,集合思想和方法是学习其他数学知识的工具。初中已经使用“自然数集合”,“整数集合”,“圆是到定点的距离相等的集合”等。集合不仅指数和点,可以是任何事物,例如????????????日常同学们对“集合”并不陌生,如上体育课时??? 老师喊:“1.2班
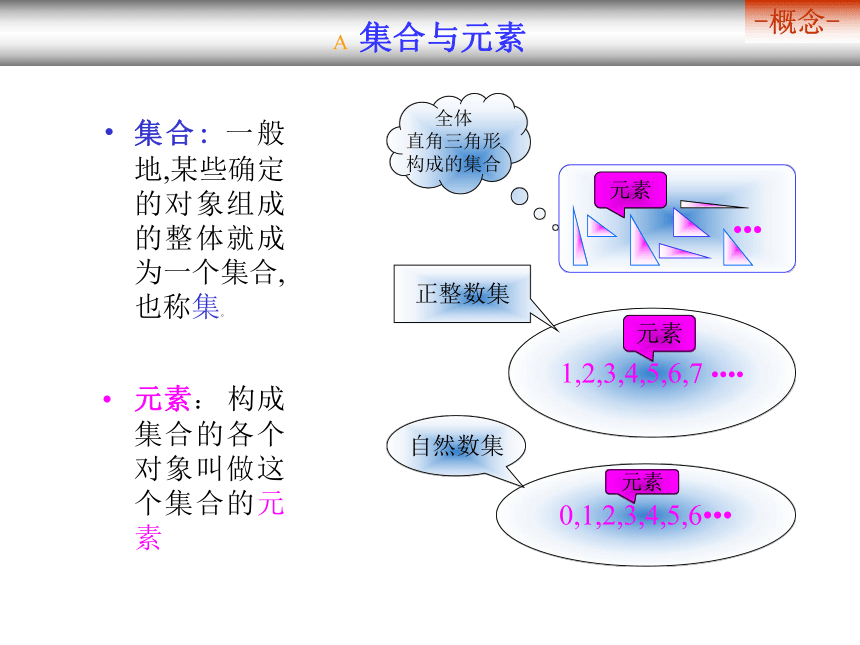
集合!”1.2班全体同学就是一个集合? 集合与元素 ? 集合与元素 集合: 一般地,某些确定的对象组成的整体就成为一个集合,也称集。-概念-元素: 构成集合的各个对象叫做这个集合的元素 ? a是集合A的元素,记作a?A。 3?A
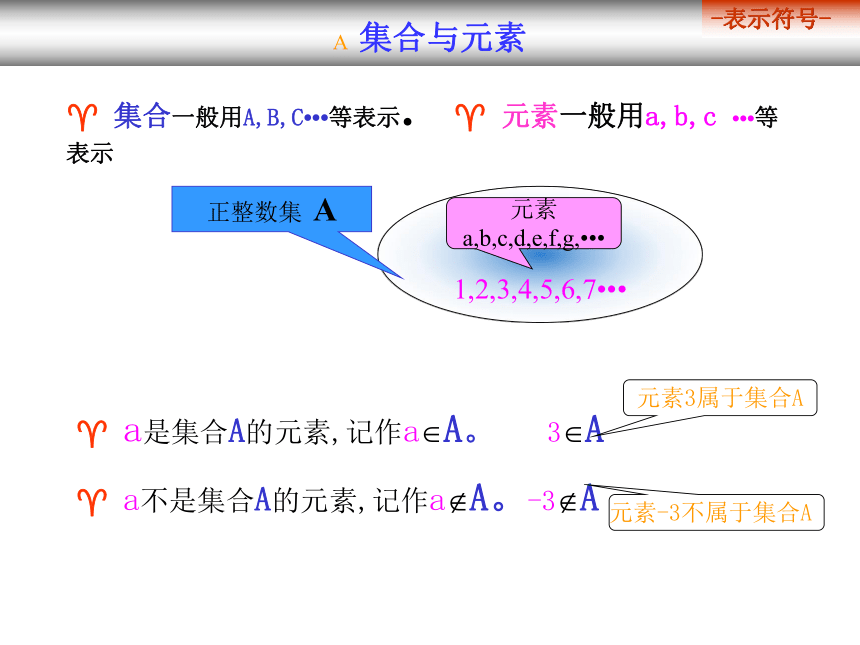
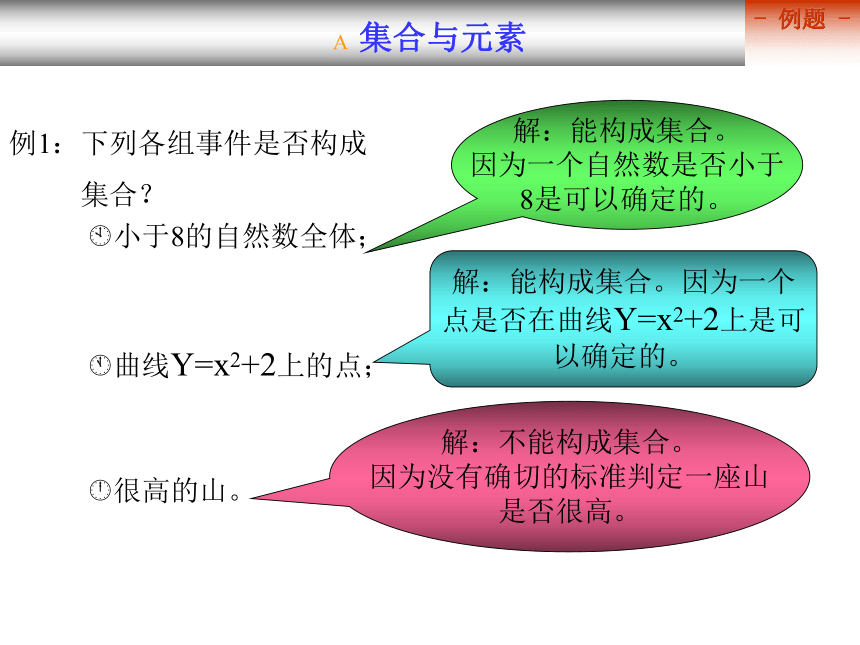
? a不是集合A的元素,记作a?A。-3?A? 集合一般用A,B,C???等表示. ? 元素一般用a,b,c ???等表示元素3属于集合A元素-3不属于集合A ? 集合与元素 -表示符号-? 集合与元素 类别特征? 集合与元素 例1:下列各组事件是否构成
集合?
?小于8的自然数全体;
?曲线Y=x2+2上的点;
?很高的山。解:能构成集合。
因为一个自然数是否小于
8是可以确定的。解:能构成集合。因为一个
点是否在曲线Y=x2+2上是可
以确定的。解:不能构成集合。
因为没有确切的标准判定一座山
是否很高。- 例题 - -5?Z -5?Q -5?R? 集合与元素 思考、例题思考题:请同学举出5个集合的例子。解:0?N 0?Z 0?Q 0?R ??Q ??R ?? R练习1:(口答)下列每组事件是否构成集合?1、我班学习较好的所有的同学;
2、全体大于-6的整数;
3、美丽的校园。?构成?不构成?不构成 ? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?? 集合与元素 - 练习 -练习3:(口答)下列给定集合各有那些元素?? 方程 x-2=3 的解构成的集合
? 小于10的正奇数构成的集合
? 一年中有31天的月份构成的集合5
1,3,5,7,9
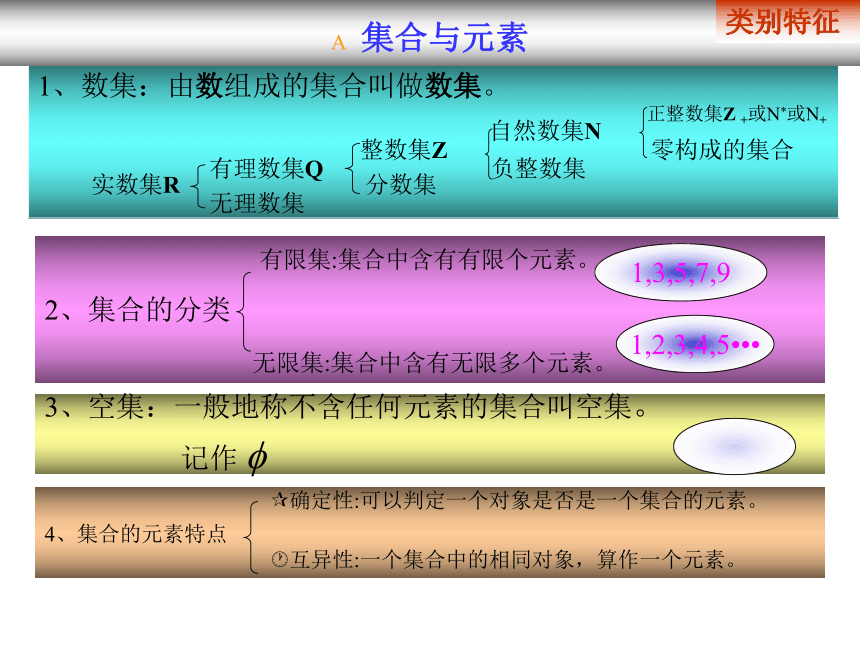
1,3,5,7,8,10,12月份? 集合与元素 练习作业小结:?元素确定性:可以判定一个对象是否是一个集合的元素。
?元素互异性:一个集合中的相同对象,算作一个元素。祝同学们进步!谢谢使用本课件集合与罗辑用与语 集合的概念本节重点:集合概念及其表示方法,子集概念本节难点:?正确运用集合两种表示法;
?分清元素与子集、属于与包含的区别主要内容:集合与元素,有限集和无限集,空集。集合思想的发展 集合论自一八九二年著名的数学家康托作奠基性工作以来,集合论思想的应用越来越广泛。
集合的概念是数学的一个基本概念,很难用更简单的概念来给他下定义只能给予一种描述,关于集合的描述是多种多样的。诸如:
“凡说到集合指的就是某些对象的汇集。”---H.A.福罗洛夫:?实变函数?“凡是具有某种特殊性质的东西的全体即称为集合。”---那汤松?实变函数论?
“凡是具有某种性质的、确定的有区别的事物的全体就是一个集合(SET)或简称集。”--- ?集合论?
“所谓集合乃是可以区别的事物的汇集”---河田敬 ?集合?拓扑?测度?
“某些指定的‘东西’ 集在一起就成为集。”---欧阳光 ?集合和应射?集合思想的发展 “若干个(有限或无限多个)固定事物的全体就是一个集叫做一个集合。”---张禾瑞?近似代数基础?
“一组对象的全体形成一个集合。”--- ?高中数学发散思维辅导?
“集合是指由一些事物的组成的整体。”--- ?职高教材?
“某些确定的对象组成的整体就成为集合。”--- ?2001职高教材?集合思想的发展
集合!”1.2班全体同学就是一个集合? 集合与元素 ? 集合与元素 集合: 一般地,某些确定的对象组成的整体就成为一个集合,也称集。-概念-元素: 构成集合的各个对象叫做这个集合的元素 ? a是集合A的元素,记作a?A。 3?A
? a不是集合A的元素,记作a?A。-3?A? 集合一般用A,B,C???等表示. ? 元素一般用a,b,c ???等表示元素3属于集合A元素-3不属于集合A ? 集合与元素 -表示符号-? 集合与元素 类别特征? 集合与元素 例1:下列各组事件是否构成
集合?
?小于8的自然数全体;
?曲线Y=x2+2上的点;
?很高的山。解:能构成集合。
因为一个自然数是否小于
8是可以确定的。解:能构成集合。因为一个
点是否在曲线Y=x2+2上是可
以确定的。解:不能构成集合。
因为没有确切的标准判定一座山
是否很高。- 例题 - -5?Z -5?Q -5?R? 集合与元素 思考、例题思考题:请同学举出5个集合的例子。解:0?N 0?Z 0?Q 0?R ??Q ??R ?? R练习1:(口答)下列每组事件是否构成集合?1、我班学习较好的所有的同学;
2、全体大于-6的整数;
3、美丽的校园。?构成?不构成?不构成 ? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?? 集合与元素 - 练习 -练习3:(口答)下列给定集合各有那些元素?? 方程 x-2=3 的解构成的集合
? 小于10的正奇数构成的集合
? 一年中有31天的月份构成的集合5
1,3,5,7,9
1,3,5,7,8,10,12月份? 集合与元素 练习作业小结:?元素确定性:可以判定一个对象是否是一个集合的元素。
?元素互异性:一个集合中的相同对象,算作一个元素。祝同学们进步!谢谢使用本课件集合与罗辑用与语 集合的概念本节重点:集合概念及其表示方法,子集概念本节难点:?正确运用集合两种表示法;
?分清元素与子集、属于与包含的区别主要内容:集合与元素,有限集和无限集,空集。集合思想的发展 集合论自一八九二年著名的数学家康托作奠基性工作以来,集合论思想的应用越来越广泛。
集合的概念是数学的一个基本概念,很难用更简单的概念来给他下定义只能给予一种描述,关于集合的描述是多种多样的。诸如:
“凡说到集合指的就是某些对象的汇集。”---H.A.福罗洛夫:?实变函数?“凡是具有某种特殊性质的东西的全体即称为集合。”---那汤松?实变函数论?
“凡是具有某种性质的、确定的有区别的事物的全体就是一个集合(SET)或简称集。”--- ?集合论?
“所谓集合乃是可以区别的事物的汇集”---河田敬 ?集合?拓扑?测度?
“某些指定的‘东西’ 集在一起就成为集。”---欧阳光 ?集合和应射?集合思想的发展 “若干个(有限或无限多个)固定事物的全体就是一个集叫做一个集合。”---张禾瑞?近似代数基础?
“一组对象的全体形成一个集合。”--- ?高中数学发散思维辅导?
“集合是指由一些事物的组成的整体。”--- ?职高教材?
“某些确定的对象组成的整体就成为集合。”--- ?2001职高教材?集合思想的发展
