2.1 生活中的变量关系 同步练习(含答案)
文档属性
| 名称 | 2.1 生活中的变量关系 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-14 00:00:00 | ||
图片预览

文档简介
2.1
生活中的变量关系
同步练习
基础巩固
?1.下列说法不正确的是( ).
A.依赖关系不一定是函数关系
B.函数关系是依赖关系
C.如果变量m是变量n的函数,那么变量n也是变量m的函数
D.如果变量m是变量n的函数,那么变量n不一定是变量m的函数
2.张大明种植了10亩小麦,每亩施肥x千克,小麦总产量y千克,则( ).
A.x,y之间有依赖关系
B.x,y之间有函数关系
C.y是x的函数
D.x是y的函数
3.星期天,小明从家出发,出去散步,图中描述了他散步过程中离家的距离s(m)与散步所用的时间t(min)之间的函数关系,根据图像,下面的描述符合小明散步情况的是( ).
A.从家出发,到一个公共阅报栏,看了一会儿报,就回家了
B.从家出发,到一个公共阅报栏,看了一会儿报后,继续向前走了一段,然后回家了
C.从家出发,散了一会儿步(没有停留),然后回家了
D.从家出发,散了一会儿步,就找同学去了,18
min后才回家
4.下列变量之间的关系是函数关系的是( ).
A.光照时间与果树亩产量
B.台风的级数与交通事故
C.水稻的产量与用肥量
D.已知二次函数y=ax2+bx+c,其中a,c是常数,取b为自变量,因变量是这个函数的判别式Δ=b2-4ac
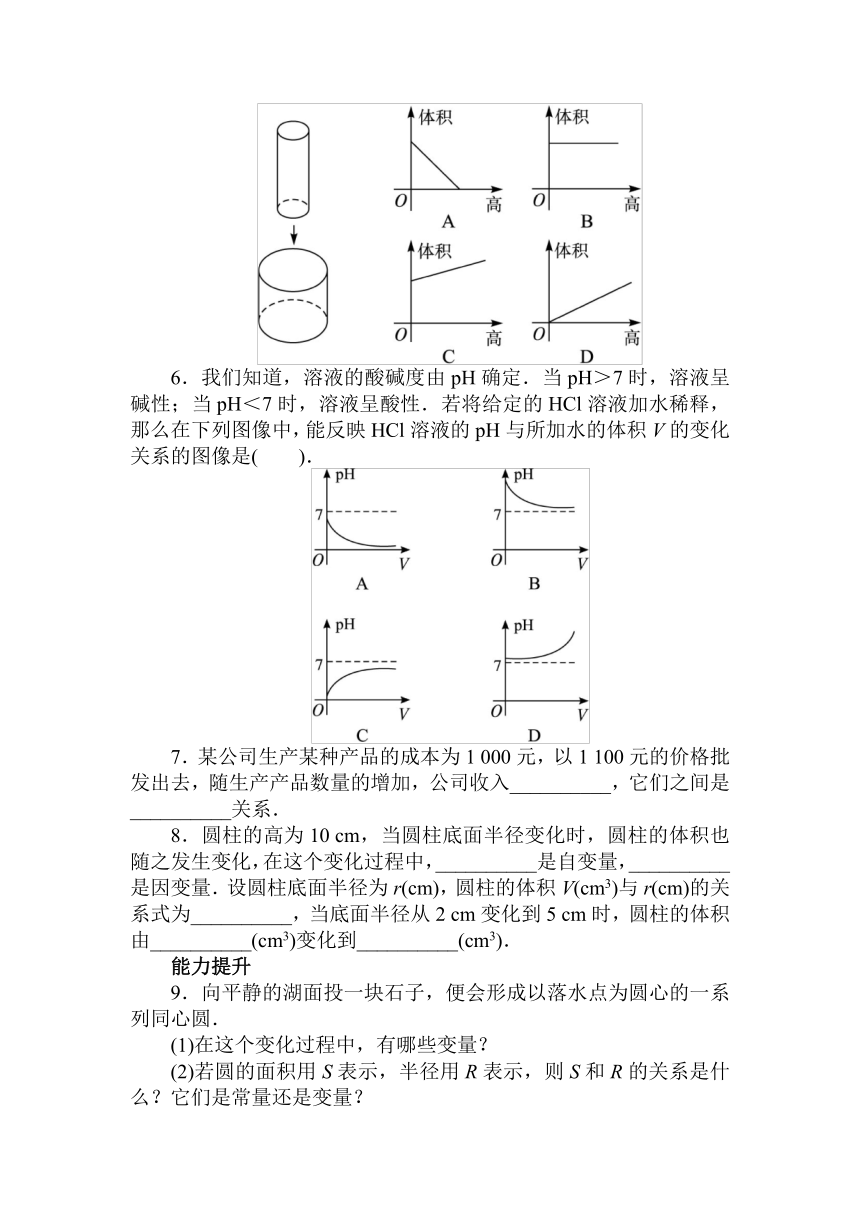
5.如图,将一个“瘦长”的圆柱钢锭经过多次锻压成一个“矮胖”的圆柱钢锭(不计损耗),则在锻压过程中,圆柱体积与高的关系可用图像表示为( ).
6.我们知道,溶液的酸碱度由pH确定.当pH>7时,溶液呈碱性;当pH<7时,溶液呈酸性.若将给定的HCl溶液加水稀释,那么在下列图像中,能反映HCl溶液的pH与所加水的体积V的变化关系的图像是( ).
7.某公司生产某种产品的成本为1
000元,以1
100元的价格批发出去,随生产产品数量的增加,公司收入__________,它们之间是__________关系.
8.圆柱的高为10
cm,当圆柱底面半径变化时,圆柱的体积也随之发生变化,在这个变化过程中,__________是自变量,__________是因变量.设圆柱底面半径为r(cm),圆柱的体积V(cm3)与r(cm)的关系式为__________,当底面半径从2
cm变化到5
cm时,圆柱的体积由__________(cm3)变化到__________(cm3).
能力提升
9.向平静的湖面投一块石子,便会形成以落水点为圆心的一系列同心圆.
(1)在这个变化过程中,有哪些变量?
(2)若圆的面积用S表示,半径用R表示,则S和R的关系是什么?它们是常量还是变量?
(3)若圆的周长用C表示,半径用R表示,则C与R的关系是什么?
10.如图表示一人骑自行车离家的距离与时间的关系.骑车者9时离开家,15时回到家,根据这个图,请你回答下列问题:
(1)最初到达离家最远的地方是什么时间?离家多远?
(2)何时开始第一次休息?休息了多长时间?
(3)第一次休息时,离家多远?
(4)11:00到12:00他骑了多少千米?
(5)他在9:00~10:00和10:00~10:30的平均速度分别是多少?
(6)他在哪段时间内停止前进并休息用午餐?
11.在工作的状态下,饮水机会通过自动对水加热使机中水的温度保持在一定范围内.下图表示在饮水机的水温达到最高后,饮水机处于工作状态中的水的温度的变化情况:
根据下图,设计一个问题,并解答所设计的问题.
参考答案
1.C 点拨:根据依赖关系与函数关系的区别可知A,B正确.若变量m是变量n的函数.因为满足函数关系的自变量n对因变量m可以是多对一,此时若把m换成自变量,n换成因变量,显然对于m的每一个取值,会有多个n与之对应,所以变量n不是变量m的函数.
2.A 点拨:虽然小麦总产量y与每亩施肥量x之间存在依赖关系,但小麦总产量y还受气候、管理等其他因素的影响,所以x,y之间无函数关系.
3.B 点拨:水平的一段线段表明小明离家的距离始终是300米,然后离家距离达到500米,说明小明从家出发后,到一个公共阅报栏,看了一会儿报后,继续向前走了一段,然后回家了.故答案为B.
4.D 点拨:果树的亩产量不仅与光照时间有关,还与施肥量、管理等因素有关,故二者不是函数关系;交通事故与很多因素有关,如道路状况、司机的技术和状态等,故这两个变量不是函数关系;同理,水稻的产量与用肥量也不是函数关系;当a,c是常数,b为自变量时,由判别式Δ=b2-4ac可以知道,对于b的每一个取值,都有唯一确定的Δ与之对应,这说明Δ是b的函数,故选D.
5.B 点拨:圆柱钢锭的体积不随高的变化而变化.
6.C 点拨:HCl溶液呈酸性,其pH值总小于7,随着加入水的体积增大,其pH值会越来越接近7.
7.增加 函数
8.圆柱底面半径 圆柱体积 V=10πr2 40π 250π
点拨:圆柱的体积为V=πr2h(其中r表示圆柱的底面半径,h表示圆柱的高).
9.解:(1)形成的一系列同心圆的半径、周长、面积都是变量.
(2)圆的面积S与半径R存在着依赖关系,对于半径R的每一个取值,都有唯一的面积S与之对应,所以圆的面积S是半径R的函数,其函数关系式是S=πR2.圆的面积S.半径R都是变量.
(3)C=2πR.
10.解:(1)最初到达离家最远的地方是在12时,此时离家30千米.
(2)10:30时开始第一次休息,休息了半小时.
(3)第一次休息时,离家17千米.
(4)从11:00到12:00,他离家的距离由17千米增加到30千米,所以他骑了13千米.
(5)在9:00~10:00行驶的路程为10千米,所用时间为1小时,他的平均速度=10(千米/时);在10:00~10:30行驶的路程为17-10=7(千米),所用时间为0.5小时,他的平均速度为=14(千米/时).
(6)在12:00~13:00停止前进并休息用午餐.
11.解:设计问题就是从图像中获取有关信息.例如,提出下列问题:
问题1:饮水机中水的最高温度是多少?最低温度是多少?
解:水的最高温度为96
℃,最低温度为91
℃.
问题2:水温上升到最高温度后,再经过10分钟饮水机中水的温度多高?35分钟时水的温度多高?
解:10分钟后水的温度约93
℃高,35分钟时水的温度约95
℃高.
问题3:哪段时间水的温度在不断下降?哪段时间水的温度在持续上升?
解:约从开始到27分钟时水的温度在不断下降,从27分钟到32分钟时水的温度在不断上升,后面又有一个相同的下降与上升的过程.
生活中的变量关系
同步练习
基础巩固
?1.下列说法不正确的是( ).
A.依赖关系不一定是函数关系
B.函数关系是依赖关系
C.如果变量m是变量n的函数,那么变量n也是变量m的函数
D.如果变量m是变量n的函数,那么变量n不一定是变量m的函数
2.张大明种植了10亩小麦,每亩施肥x千克,小麦总产量y千克,则( ).
A.x,y之间有依赖关系
B.x,y之间有函数关系
C.y是x的函数
D.x是y的函数
3.星期天,小明从家出发,出去散步,图中描述了他散步过程中离家的距离s(m)与散步所用的时间t(min)之间的函数关系,根据图像,下面的描述符合小明散步情况的是( ).
A.从家出发,到一个公共阅报栏,看了一会儿报,就回家了
B.从家出发,到一个公共阅报栏,看了一会儿报后,继续向前走了一段,然后回家了
C.从家出发,散了一会儿步(没有停留),然后回家了
D.从家出发,散了一会儿步,就找同学去了,18
min后才回家
4.下列变量之间的关系是函数关系的是( ).
A.光照时间与果树亩产量
B.台风的级数与交通事故
C.水稻的产量与用肥量
D.已知二次函数y=ax2+bx+c,其中a,c是常数,取b为自变量,因变量是这个函数的判别式Δ=b2-4ac
5.如图,将一个“瘦长”的圆柱钢锭经过多次锻压成一个“矮胖”的圆柱钢锭(不计损耗),则在锻压过程中,圆柱体积与高的关系可用图像表示为( ).
6.我们知道,溶液的酸碱度由pH确定.当pH>7时,溶液呈碱性;当pH<7时,溶液呈酸性.若将给定的HCl溶液加水稀释,那么在下列图像中,能反映HCl溶液的pH与所加水的体积V的变化关系的图像是( ).
7.某公司生产某种产品的成本为1
000元,以1
100元的价格批发出去,随生产产品数量的增加,公司收入__________,它们之间是__________关系.
8.圆柱的高为10
cm,当圆柱底面半径变化时,圆柱的体积也随之发生变化,在这个变化过程中,__________是自变量,__________是因变量.设圆柱底面半径为r(cm),圆柱的体积V(cm3)与r(cm)的关系式为__________,当底面半径从2
cm变化到5
cm时,圆柱的体积由__________(cm3)变化到__________(cm3).
能力提升
9.向平静的湖面投一块石子,便会形成以落水点为圆心的一系列同心圆.
(1)在这个变化过程中,有哪些变量?
(2)若圆的面积用S表示,半径用R表示,则S和R的关系是什么?它们是常量还是变量?
(3)若圆的周长用C表示,半径用R表示,则C与R的关系是什么?
10.如图表示一人骑自行车离家的距离与时间的关系.骑车者9时离开家,15时回到家,根据这个图,请你回答下列问题:
(1)最初到达离家最远的地方是什么时间?离家多远?
(2)何时开始第一次休息?休息了多长时间?
(3)第一次休息时,离家多远?
(4)11:00到12:00他骑了多少千米?
(5)他在9:00~10:00和10:00~10:30的平均速度分别是多少?
(6)他在哪段时间内停止前进并休息用午餐?
11.在工作的状态下,饮水机会通过自动对水加热使机中水的温度保持在一定范围内.下图表示在饮水机的水温达到最高后,饮水机处于工作状态中的水的温度的变化情况:
根据下图,设计一个问题,并解答所设计的问题.
参考答案
1.C 点拨:根据依赖关系与函数关系的区别可知A,B正确.若变量m是变量n的函数.因为满足函数关系的自变量n对因变量m可以是多对一,此时若把m换成自变量,n换成因变量,显然对于m的每一个取值,会有多个n与之对应,所以变量n不是变量m的函数.
2.A 点拨:虽然小麦总产量y与每亩施肥量x之间存在依赖关系,但小麦总产量y还受气候、管理等其他因素的影响,所以x,y之间无函数关系.
3.B 点拨:水平的一段线段表明小明离家的距离始终是300米,然后离家距离达到500米,说明小明从家出发后,到一个公共阅报栏,看了一会儿报后,继续向前走了一段,然后回家了.故答案为B.
4.D 点拨:果树的亩产量不仅与光照时间有关,还与施肥量、管理等因素有关,故二者不是函数关系;交通事故与很多因素有关,如道路状况、司机的技术和状态等,故这两个变量不是函数关系;同理,水稻的产量与用肥量也不是函数关系;当a,c是常数,b为自变量时,由判别式Δ=b2-4ac可以知道,对于b的每一个取值,都有唯一确定的Δ与之对应,这说明Δ是b的函数,故选D.
5.B 点拨:圆柱钢锭的体积不随高的变化而变化.
6.C 点拨:HCl溶液呈酸性,其pH值总小于7,随着加入水的体积增大,其pH值会越来越接近7.
7.增加 函数
8.圆柱底面半径 圆柱体积 V=10πr2 40π 250π
点拨:圆柱的体积为V=πr2h(其中r表示圆柱的底面半径,h表示圆柱的高).
9.解:(1)形成的一系列同心圆的半径、周长、面积都是变量.
(2)圆的面积S与半径R存在着依赖关系,对于半径R的每一个取值,都有唯一的面积S与之对应,所以圆的面积S是半径R的函数,其函数关系式是S=πR2.圆的面积S.半径R都是变量.
(3)C=2πR.
10.解:(1)最初到达离家最远的地方是在12时,此时离家30千米.
(2)10:30时开始第一次休息,休息了半小时.
(3)第一次休息时,离家17千米.
(4)从11:00到12:00,他离家的距离由17千米增加到30千米,所以他骑了13千米.
(5)在9:00~10:00行驶的路程为10千米,所用时间为1小时,他的平均速度=10(千米/时);在10:00~10:30行驶的路程为17-10=7(千米),所用时间为0.5小时,他的平均速度为=14(千米/时).
(6)在12:00~13:00停止前进并休息用午餐.
11.解:设计问题就是从图像中获取有关信息.例如,提出下列问题:
问题1:饮水机中水的最高温度是多少?最低温度是多少?
解:水的最高温度为96
℃,最低温度为91
℃.
问题2:水温上升到最高温度后,再经过10分钟饮水机中水的温度多高?35分钟时水的温度多高?
解:10分钟后水的温度约93
℃高,35分钟时水的温度约95
℃高.
问题3:哪段时间水的温度在不断下降?哪段时间水的温度在持续上升?
解:约从开始到27分钟时水的温度在不断下降,从27分钟到32分钟时水的温度在不断上升,后面又有一个相同的下降与上升的过程.
