2.1 生活中的变量关系 学案5(含答案)
文档属性
| 名称 | 2.1 生活中的变量关系 学案5(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-14 10:48:39 | ||
图片预览


文档简介
2.1
生活中的变量关系
学案
1.常量与变量的区分
在研究某一问题的变化过程中,数值保持不变的量称为常量,可以取不同数值的量称为变量.
谈重点
正确理解常量与变量
可结合生活中的实例,用辩证的观点来理解常量与变量,常量是相对于某一过程或另一个变量而言的,绝对的常量是没有的,因为物质的运动是绝对的,静止是相对的,所以物动则变.在我们的生活中容易找出众多的实例,如:
(1)匀速直线运动中,速度是常量,时间和路程均为变量,但在实际运动过程中,绝对的匀速是没有的,因为人驾驶汽车在行驶过程中,不可避免地要进行加速、减速或刹车等操作.
(2)电影院里,对某一场次和座位类别而言,票价是常量,而售票张数和收入均为变量.但相对于某个较长时间的间隔而言,由于演出的内容、种类、档次的不同,其票价仍是一个变量.
由此可以看出,常量具有相对性,而变量是永恒的,是大量存在的.
【例1】一辆汽车由南京驶往相距300千米的上海,它的平均速度是100千米/时,则汽车距上海的路程s(千米)与行驶时间t(时)的关系是s=300-100t,在这里,常量是______,变量是______.
解析:判断常量与变量的关键是看它是否发生了变化,在这里,常量是南京与上海的距离300千米和汽车行驶的平均速度100千米/时,变量是汽车在行驶过程中距上海的路程s和行驶时间t.
答案:300,-100 s,t
2.生活中的变量关系及判断
生活中的两个变量之间可能具有依赖关系,也可能不具有依赖关系,具有依赖关系的两个变量可能是函数关系,也可能是非函数关系.
(1)依赖关系:在某变化过程中有两个变量,如果其中一个变量的值发生了变化,另一个变量的值也会随之发生变化,那么就称这两个变量具有依赖关系.特别地,如果对于其中一个变量的每一个值,另一个变量都有唯一确定的值与之对应,那么就称这两个变量之间有函数关系.
(2)非依赖关系:在某变化过程中有两个变量,如果其中一个变量的值发生了变化,另一个变量的值不会发生任何变化,那么就称这两个变量具有非依赖关系.
(3)依赖关系和函数关系的联系与区别:
函数关系是特殊的依赖关系,具有依赖关系的两个变量有的是函数关系,有的不是函数关系.因此说依赖关系不一定是函数关系,而函数关系一定是依赖关系.
例如,积雪层对越冬作物具有防冻保暖作用,大雪可以防止土壤中的热量向外散发,又可阻止外界冷空气的侵入,具有增墒肥田作用.所以下雪与来年的丰收具有依赖关系.又因为作物的丰收还受其他因素的影响,如天气、施肥量等,所以下雪与来年的丰收不具有函数关系.
破疑点
判断两个有依赖关系的变量之间是否是函数关系的步骤
①确定因变量和自变量;②判断对于自变量的每一个取值,是否都有唯一的因变量与之对应.若满足这个条件则是函数关系,否则不是.这里要特别注意的是,满足函数关系的自变量对因变量,可以一对一,也可以多对一,但不可以一对多.
【例2】下列过程中,各变量之间是否存在依赖关系?其中哪些是函数关系?
(1)将保温瓶中的热水倒入茶杯中缓慢冷却,并将一温度计放入茶杯中,每隔一段时间,观察温度计示数的变化.冷却时间与温度计示数的关系;
(2)做自由落体运动的物体下落的距离与时间的关系;
(3)商品的销售额与广告费之间的关系;
(4)家庭的食品支出与电视价格之间的关系;
(5)在高速公路上行驶的汽车所走的路程与时间的关系.
分析:两个变量中的一个变量发生变化时,根据另一个变量是否发生变化来确定依赖关系;根据另一个变量发生变化且取值唯一来确定函数关系.
解:(1)温度计示数随冷却时间的变化而变化,所以冷却时间与温度计示数存在着依赖关系.又因为对于冷却时间的每一个取值,都有唯一的温度计示数与之对应,所以,温度计示数是冷却时间的函数;(2)科学家通过实验发现,做自由落体运动的物体下落的距离(h)与时间(t)具有关系,其中g是常量,很显然,对于时间t在其变化范围内的每一个取值,都有唯一的下落距离h与之对应,故这两个变量存在依赖关系,且距离是时间的函数;(3)商品的销售额与广告费这两个变量在现实生活中存在依赖关系,但商品的销售额还受其他因素的影响,比如产品的质量、价格、售后服务等,所以商品的销售额与广告费之间不是函数关系;(4)家庭的食品支出与电视价格之间不存在依赖关系;(5)在高速公路上行驶的汽车所走路程(因变量)随时间(自变量)的变化而变化,所以它们之间存在着依赖关系,且路程是时间的函数.
综上可知,(1)(2)(5)中的变量间存在依赖关系,且是函数关系;(3)中变量间存在依赖关系,不是函数关系;(4)中两个变量间不存在依赖关系.
解技巧
如何判断两个变量之间是否存在依赖关系
判断两个变量之间是否存在依赖关系,只需看一个变量发生变化时,另一个变量是否会随之变化;判断两个具有依赖关系的变量是否是函数关系,关键是看二者之间的关系是否具有确定性,即验证对于一个变量的每一个值,另一个变量是否都有唯一确定的值与之对应.
3.生活中变量关系的表示
(1)通过图像反映两变量之间的关系
用图像反映两变量间的关系是一种常用的表示两变量关系的方式.在解此类题时要能从图中找到两个变量,并能判断它们之间的相互依赖关系是如何变化的.
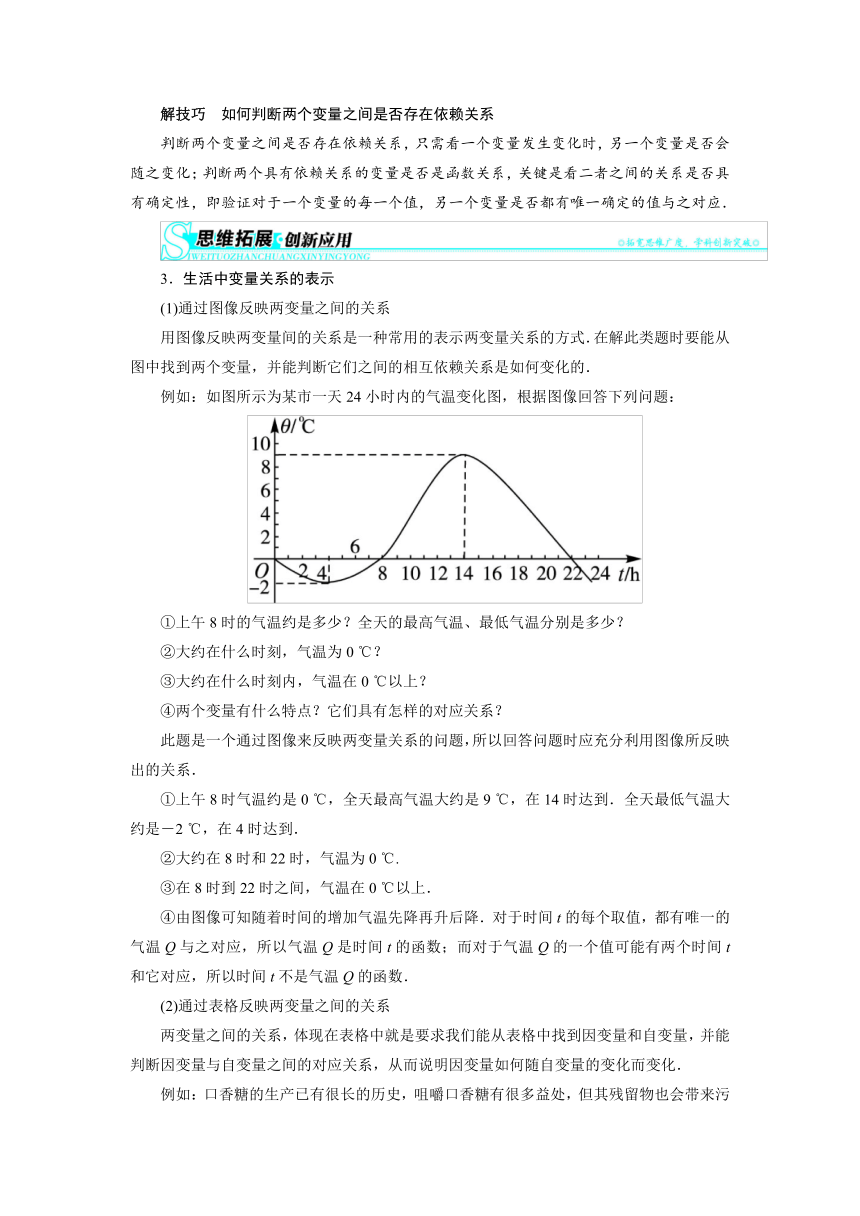
例如:如图所示为某市一天24小时内的气温变化图,根据图像回答下列问题:
①上午8时的气温约是多少?全天的最高气温、最低气温分别是多少?
②大约在什么时刻,气温为0
℃?
③大约在什么时刻内,气温在0
℃以上?
④两个变量有什么特点?它们具有怎样的对应关系?
此题是一个通过图像来反映两变量关系的问题,所以回答问题时应充分利用图像所反映出的关系.
①上午8时气温约是0
℃,全天最高气温大约是9
℃,在14时达到.全天最低气温大约是-2
℃,在4时达到.
②大约在8时和22时,气温为0
℃.
③在8时到22时之间,气温在0
℃以上.
④由图像可知随着时间的增加气温先降再升后降.对于时间t的每个取值,都有唯一的气温Q与之对应,所以气温Q是时间t的函数;而对于气温Q的一个值可能有两个时间t和它对应,所以时间t不是气温Q的函数.
(2)通过表格反映两变量之间的关系
两变量之间的关系,体现在表格中就是要求我们能从表格中找到因变量和自变量,并能判断因变量与自变量之间的对应关系,从而说明因变量如何随自变量的变化而变化.
例如:口香糖的生产已有很长的历史,咀嚼口香糖有很多益处,但其残留物也会带来污染,为了研究口香糖的黏附力与温度的关系,一位同学通过实验,测定了在不同温度下除去糖分的口香糖与瓷砖地面的黏附力,得到了如下表所示的一组数据:
请回答下列问题:
①请根据上述数据,绘制出口香糖黏附力F随温度t变化的图像.
②根据上述数据以及得到的图像,你得到怎样的实验结论?
根据表中数据的范围绘制出F随t变化的图像如右图,于是可得实验结论:①随着温度的升高,口香糖的黏附力先增大后减小;②当温度在约37
℃时,口香糖的黏附力最大;当温度在50
℃时,黏附力最小.所以可通过加热的办法除去磁砖上的口香糖残留物.
【例3-1】如图1是一辆汽车的速度随时间而变化的示意图.
图1
(1)汽车从出发到最后停止共经过多少时间?它的最高时速是多少?
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)如果纵轴换成路程s(千米),横轴表示时间t(时),如图2是一个骑自行车者离家距离与时间的关系图像.在出发后8时到10时之间可能发生了什么情况?骑自行车者在哪些时间段保持匀速运动?速度分别是多少?
图2
分析:解用图像反映两变量之间关系的题目的关键是识图,弄清两个变量之间的关系.
解:(1)汽车从出发到最后停止共经过了24分钟,它的最高时速是80千米/时.
(2)汽车在出发后2分钟到6分钟,18分钟到22分钟均保持匀速行驶,时速分别为30千米/时和80千米/时.
(3)出发后8分到10分之间汽车速度为0千米/时,重新启动后,车速很快提高到80千米/时,因此在这段时间内很可能在修车、加油等.
(4)在出发后8时到10时之间骑自行车者可能回家吃饭、休息等.骑自行车者在开始出发到出发后2小时时间段内匀速运动,车速为(千米/时);在出发后6小时到8小时时间段内匀速运动,车速为(千米/时);在出发后10小时到18小时时间段匀速运动,车速为(千米/时);在出发后22小时到24小时时间段内匀速运动,车速为(千米/时).
【例3-2】从市场中了解到,饰用K金的含金量如下表:
K数
含金量(%)
24K
99以上
22K
91.7
21K
87.5
18K
75
14K
58.5
12K
50
10K
41.66
9K
37.5
8K
33.34
6K
25
饰用K金的K数与含金量之间是________关系,K数越大含金量________.
解析:通过表格可知,饰用K金的含金量随着K数的减小而减小,对于K数的每一个取值,都有唯一的含金量与之对应,所以含金量是K数的函数,饰用K金的K数与含金量之间是函数关系,且K数越大含金量越高.
答案:函数 越高
生活中的变量关系
学案
1.常量与变量的区分
在研究某一问题的变化过程中,数值保持不变的量称为常量,可以取不同数值的量称为变量.
谈重点
正确理解常量与变量
可结合生活中的实例,用辩证的观点来理解常量与变量,常量是相对于某一过程或另一个变量而言的,绝对的常量是没有的,因为物质的运动是绝对的,静止是相对的,所以物动则变.在我们的生活中容易找出众多的实例,如:
(1)匀速直线运动中,速度是常量,时间和路程均为变量,但在实际运动过程中,绝对的匀速是没有的,因为人驾驶汽车在行驶过程中,不可避免地要进行加速、减速或刹车等操作.
(2)电影院里,对某一场次和座位类别而言,票价是常量,而售票张数和收入均为变量.但相对于某个较长时间的间隔而言,由于演出的内容、种类、档次的不同,其票价仍是一个变量.
由此可以看出,常量具有相对性,而变量是永恒的,是大量存在的.
【例1】一辆汽车由南京驶往相距300千米的上海,它的平均速度是100千米/时,则汽车距上海的路程s(千米)与行驶时间t(时)的关系是s=300-100t,在这里,常量是______,变量是______.
解析:判断常量与变量的关键是看它是否发生了变化,在这里,常量是南京与上海的距离300千米和汽车行驶的平均速度100千米/时,变量是汽车在行驶过程中距上海的路程s和行驶时间t.
答案:300,-100 s,t
2.生活中的变量关系及判断
生活中的两个变量之间可能具有依赖关系,也可能不具有依赖关系,具有依赖关系的两个变量可能是函数关系,也可能是非函数关系.
(1)依赖关系:在某变化过程中有两个变量,如果其中一个变量的值发生了变化,另一个变量的值也会随之发生变化,那么就称这两个变量具有依赖关系.特别地,如果对于其中一个变量的每一个值,另一个变量都有唯一确定的值与之对应,那么就称这两个变量之间有函数关系.
(2)非依赖关系:在某变化过程中有两个变量,如果其中一个变量的值发生了变化,另一个变量的值不会发生任何变化,那么就称这两个变量具有非依赖关系.
(3)依赖关系和函数关系的联系与区别:
函数关系是特殊的依赖关系,具有依赖关系的两个变量有的是函数关系,有的不是函数关系.因此说依赖关系不一定是函数关系,而函数关系一定是依赖关系.
例如,积雪层对越冬作物具有防冻保暖作用,大雪可以防止土壤中的热量向外散发,又可阻止外界冷空气的侵入,具有增墒肥田作用.所以下雪与来年的丰收具有依赖关系.又因为作物的丰收还受其他因素的影响,如天气、施肥量等,所以下雪与来年的丰收不具有函数关系.
破疑点
判断两个有依赖关系的变量之间是否是函数关系的步骤
①确定因变量和自变量;②判断对于自变量的每一个取值,是否都有唯一的因变量与之对应.若满足这个条件则是函数关系,否则不是.这里要特别注意的是,满足函数关系的自变量对因变量,可以一对一,也可以多对一,但不可以一对多.
【例2】下列过程中,各变量之间是否存在依赖关系?其中哪些是函数关系?
(1)将保温瓶中的热水倒入茶杯中缓慢冷却,并将一温度计放入茶杯中,每隔一段时间,观察温度计示数的变化.冷却时间与温度计示数的关系;
(2)做自由落体运动的物体下落的距离与时间的关系;
(3)商品的销售额与广告费之间的关系;
(4)家庭的食品支出与电视价格之间的关系;
(5)在高速公路上行驶的汽车所走的路程与时间的关系.
分析:两个变量中的一个变量发生变化时,根据另一个变量是否发生变化来确定依赖关系;根据另一个变量发生变化且取值唯一来确定函数关系.
解:(1)温度计示数随冷却时间的变化而变化,所以冷却时间与温度计示数存在着依赖关系.又因为对于冷却时间的每一个取值,都有唯一的温度计示数与之对应,所以,温度计示数是冷却时间的函数;(2)科学家通过实验发现,做自由落体运动的物体下落的距离(h)与时间(t)具有关系,其中g是常量,很显然,对于时间t在其变化范围内的每一个取值,都有唯一的下落距离h与之对应,故这两个变量存在依赖关系,且距离是时间的函数;(3)商品的销售额与广告费这两个变量在现实生活中存在依赖关系,但商品的销售额还受其他因素的影响,比如产品的质量、价格、售后服务等,所以商品的销售额与广告费之间不是函数关系;(4)家庭的食品支出与电视价格之间不存在依赖关系;(5)在高速公路上行驶的汽车所走路程(因变量)随时间(自变量)的变化而变化,所以它们之间存在着依赖关系,且路程是时间的函数.
综上可知,(1)(2)(5)中的变量间存在依赖关系,且是函数关系;(3)中变量间存在依赖关系,不是函数关系;(4)中两个变量间不存在依赖关系.
解技巧
如何判断两个变量之间是否存在依赖关系
判断两个变量之间是否存在依赖关系,只需看一个变量发生变化时,另一个变量是否会随之变化;判断两个具有依赖关系的变量是否是函数关系,关键是看二者之间的关系是否具有确定性,即验证对于一个变量的每一个值,另一个变量是否都有唯一确定的值与之对应.
3.生活中变量关系的表示
(1)通过图像反映两变量之间的关系
用图像反映两变量间的关系是一种常用的表示两变量关系的方式.在解此类题时要能从图中找到两个变量,并能判断它们之间的相互依赖关系是如何变化的.
例如:如图所示为某市一天24小时内的气温变化图,根据图像回答下列问题:
①上午8时的气温约是多少?全天的最高气温、最低气温分别是多少?
②大约在什么时刻,气温为0
℃?
③大约在什么时刻内,气温在0
℃以上?
④两个变量有什么特点?它们具有怎样的对应关系?
此题是一个通过图像来反映两变量关系的问题,所以回答问题时应充分利用图像所反映出的关系.
①上午8时气温约是0
℃,全天最高气温大约是9
℃,在14时达到.全天最低气温大约是-2
℃,在4时达到.
②大约在8时和22时,气温为0
℃.
③在8时到22时之间,气温在0
℃以上.
④由图像可知随着时间的增加气温先降再升后降.对于时间t的每个取值,都有唯一的气温Q与之对应,所以气温Q是时间t的函数;而对于气温Q的一个值可能有两个时间t和它对应,所以时间t不是气温Q的函数.
(2)通过表格反映两变量之间的关系
两变量之间的关系,体现在表格中就是要求我们能从表格中找到因变量和自变量,并能判断因变量与自变量之间的对应关系,从而说明因变量如何随自变量的变化而变化.
例如:口香糖的生产已有很长的历史,咀嚼口香糖有很多益处,但其残留物也会带来污染,为了研究口香糖的黏附力与温度的关系,一位同学通过实验,测定了在不同温度下除去糖分的口香糖与瓷砖地面的黏附力,得到了如下表所示的一组数据:
请回答下列问题:
①请根据上述数据,绘制出口香糖黏附力F随温度t变化的图像.
②根据上述数据以及得到的图像,你得到怎样的实验结论?
根据表中数据的范围绘制出F随t变化的图像如右图,于是可得实验结论:①随着温度的升高,口香糖的黏附力先增大后减小;②当温度在约37
℃时,口香糖的黏附力最大;当温度在50
℃时,黏附力最小.所以可通过加热的办法除去磁砖上的口香糖残留物.
【例3-1】如图1是一辆汽车的速度随时间而变化的示意图.
图1
(1)汽车从出发到最后停止共经过多少时间?它的最高时速是多少?
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)如果纵轴换成路程s(千米),横轴表示时间t(时),如图2是一个骑自行车者离家距离与时间的关系图像.在出发后8时到10时之间可能发生了什么情况?骑自行车者在哪些时间段保持匀速运动?速度分别是多少?
图2
分析:解用图像反映两变量之间关系的题目的关键是识图,弄清两个变量之间的关系.
解:(1)汽车从出发到最后停止共经过了24分钟,它的最高时速是80千米/时.
(2)汽车在出发后2分钟到6分钟,18分钟到22分钟均保持匀速行驶,时速分别为30千米/时和80千米/时.
(3)出发后8分到10分之间汽车速度为0千米/时,重新启动后,车速很快提高到80千米/时,因此在这段时间内很可能在修车、加油等.
(4)在出发后8时到10时之间骑自行车者可能回家吃饭、休息等.骑自行车者在开始出发到出发后2小时时间段内匀速运动,车速为(千米/时);在出发后6小时到8小时时间段内匀速运动,车速为(千米/时);在出发后10小时到18小时时间段匀速运动,车速为(千米/时);在出发后22小时到24小时时间段内匀速运动,车速为(千米/时).
【例3-2】从市场中了解到,饰用K金的含金量如下表:
K数
含金量(%)
24K
99以上
22K
91.7
21K
87.5
18K
75
14K
58.5
12K
50
10K
41.66
9K
37.5
8K
33.34
6K
25
饰用K金的K数与含金量之间是________关系,K数越大含金量________.
解析:通过表格可知,饰用K金的含金量随着K数的减小而减小,对于K数的每一个取值,都有唯一的含金量与之对应,所以含金量是K数的函数,饰用K金的K数与含金量之间是函数关系,且K数越大含金量越高.
答案:函数 越高
