江苏省张家港市塘桥初级中学(苏科版)数学八年级上册课件:第六章 一次函数专题复习2 (共13张PPT)
文档属性
| 名称 | 江苏省张家港市塘桥初级中学(苏科版)数学八年级上册课件:第六章 一次函数专题复习2 (共13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 108.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-12 17:48:01 | ||
图片预览





文档简介
课件13张PPT。一次函数与几何图形 回味练习1、已知一次函数 ,
(1)若y随x的增大而增大,则 m ;
(2)若函数图象与y轴的负半轴相交,
则m ;
(3)若函数图象经过第一、三、四象限,
则m ;
(4)若函数图象经过原点,则m .<<1且m≠ <=13、直线y=x和直线y=-2x+6的交点P的坐标是 .2、直线y= - 与x轴的交点坐标为 ,
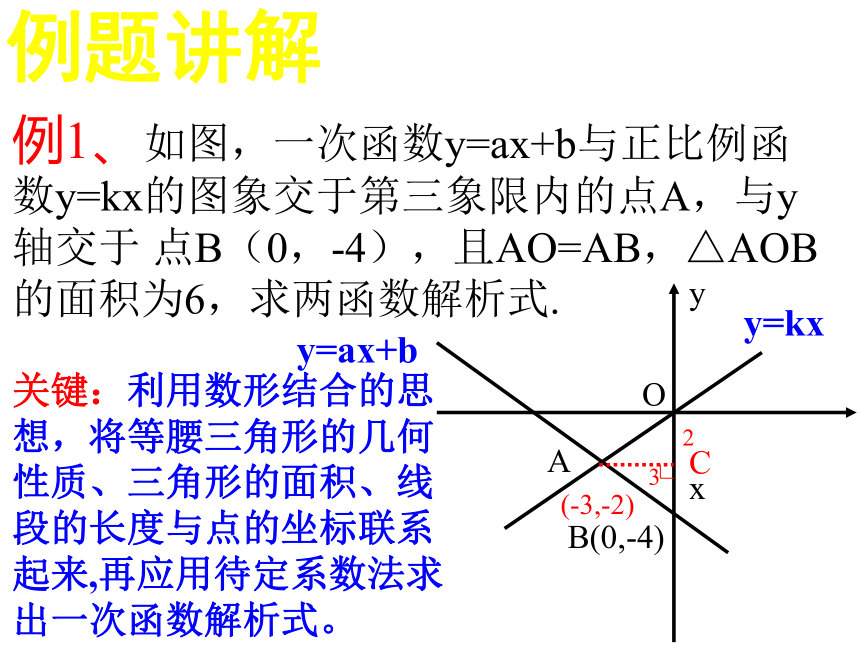
与y轴的交点坐标为 . (2,2)(6,0)(0,8)回味练习例1、如图,一次函数y=ax+b与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于 点B(0,-4),且AO=AB,△AOB的面积为6,求两函数解析式.xyOAB(0,-4)C23(-3,-2)y=kxy=ax+b例题讲解关键:利用数形结合的思想,将等腰三角形的几何性质、三角形的面积、线段的长度与点的坐标联系起来,再应用待定系数法求出一次函数解析式。例2、四边形OABC是一张放在平面直角坐标系中的矩形纸片,O点为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.如图,在AB上取一点M,使得△CBM沿CM 翻折后,点B落在X轴上,记作B’点.
(1)点B’ 的坐标为 ;
(2)求线段CM的解析式. 例题讲解(8,0)例3、如图,直线OC、BC的函数关系式分别
为y=x和y=-2x+6,动点P(x,0)在OB上
移动(0(1)点C的坐标为 ;
(2)设△OBC中位于直线L左侧部分的
面积为S,写出S与x之间的函数关系式;
(3)当x为何值时,直线L平分△BOC的
面积?例题讲解(2,2)Q通过本节课的学习,我们有哪些收获?交流会:小结: 1、在求一次函数解析式时,一般有两个待定系数,因此,只要给出两个独立条件,就可求出它的解析式.当题目中出现线段长度、三角形面积等几何条件时,通常是把它转化为点的坐标后代入解析式,求出未知系数,得出函数解析式.1、数缺形时少直观,
形少数时难入微. 数学思想:2、分类讨论1、若一次函数的图象交x轴于点A(-6,0),交正比例函数的图象于点B,且点B在第二象限,它的横坐标为- 4,又知:S△AOB=15,求直线AB的解析式. 体验练习2、如图,一次函数y=kx+b的图象与x轴、y轴分别交于点A(6,0)和B(0,2),线段AB的垂直平分线交x轴于点C,交AB于点D,
(1)求这个一次函数的关系式;
(2)求点C的坐标.x体验练习如图,直线y= 与x轴、y轴分别相交于 点A、B, 以线段AB为直角边在第一象限内 作等腰Rt△ABC,∠BAC=900,如果 点 P(1,a)为坐标系中的一 个动点. (1)求△ABC的面积; (2)证明不论a取任何实数△BOP是一个常数;(3)要使△ABP的面积与△ABC的面积相等, 求a的值.思考题时间是由分秒积成的,善于利用零星时间的人,才会做出更大的成绩来. 珍惜时间
(1)若y随x的增大而增大,则 m ;
(2)若函数图象与y轴的负半轴相交,
则m ;
(3)若函数图象经过第一、三、四象限,
则m ;
(4)若函数图象经过原点,则m .<<1且m≠ <=13、直线y=x和直线y=-2x+6的交点P的坐标是 .2、直线y= - 与x轴的交点坐标为 ,
与y轴的交点坐标为 . (2,2)(6,0)(0,8)回味练习例1、如图,一次函数y=ax+b与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于 点B(0,-4),且AO=AB,△AOB的面积为6,求两函数解析式.xyOAB(0,-4)C23(-3,-2)y=kxy=ax+b例题讲解关键:利用数形结合的思想,将等腰三角形的几何性质、三角形的面积、线段的长度与点的坐标联系起来,再应用待定系数法求出一次函数解析式。例2、四边形OABC是一张放在平面直角坐标系中的矩形纸片,O点为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.如图,在AB上取一点M,使得△CBM沿CM 翻折后,点B落在X轴上,记作B’点.
(1)点B’ 的坐标为 ;
(2)求线段CM的解析式. 例题讲解(8,0)例3、如图,直线OC、BC的函数关系式分别
为y=x和y=-2x+6,动点P(x,0)在OB上
移动(0
(2)设△OBC中位于直线L左侧部分的
面积为S,写出S与x之间的函数关系式;
(3)当x为何值时,直线L平分△BOC的
面积?例题讲解(2,2)Q通过本节课的学习,我们有哪些收获?交流会:小结: 1、在求一次函数解析式时,一般有两个待定系数,因此,只要给出两个独立条件,就可求出它的解析式.当题目中出现线段长度、三角形面积等几何条件时,通常是把它转化为点的坐标后代入解析式,求出未知系数,得出函数解析式.1、数缺形时少直观,
形少数时难入微. 数学思想:2、分类讨论1、若一次函数的图象交x轴于点A(-6,0),交正比例函数的图象于点B,且点B在第二象限,它的横坐标为- 4,又知:S△AOB=15,求直线AB的解析式. 体验练习2、如图,一次函数y=kx+b的图象与x轴、y轴分别交于点A(6,0)和B(0,2),线段AB的垂直平分线交x轴于点C,交AB于点D,
(1)求这个一次函数的关系式;
(2)求点C的坐标.x体验练习如图,直线y= 与x轴、y轴分别相交于 点A、B, 以线段AB为直角边在第一象限内 作等腰Rt△ABC,∠BAC=900,如果 点 P(1,a)为坐标系中的一 个动点. (1)求△ABC的面积; (2)证明不论a取任何实数△BOP是一个常数;(3)要使△ABP的面积与△ABC的面积相等, 求a的值.思考题时间是由分秒积成的,善于利用零星时间的人,才会做出更大的成绩来. 珍惜时间
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
