2.2.1-2.2.2 函数的概念及其表示法 学案(含答案)
文档属性
| 名称 | 2.2.1-2.2.2 函数的概念及其表示法 学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 59.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-14 14:18:36 | ||
图片预览


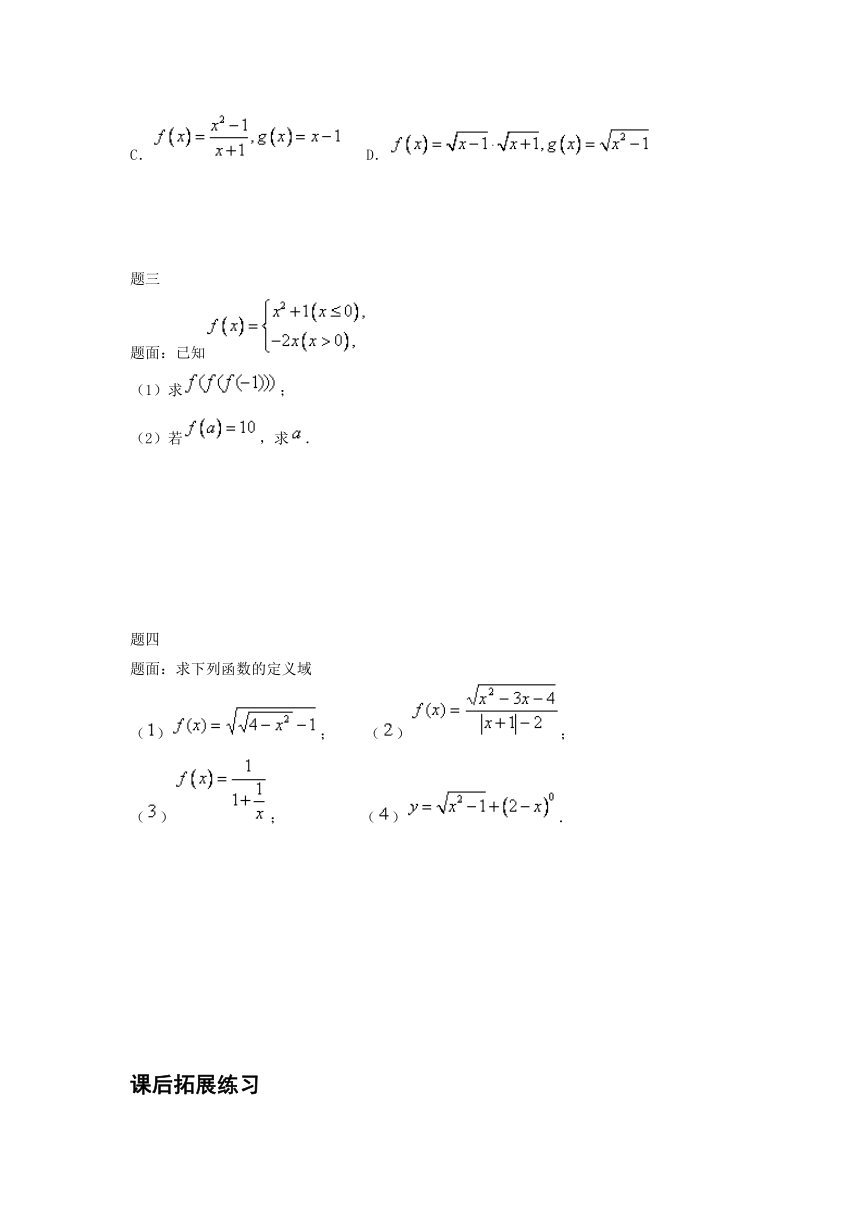
文档简介
2.2.1-2.2.2
函数的概念及其表示法
学案
主要考点梳理
1.函数定义
设是非空数集,如果按照某个确定的对应关系,使对应集合中的任意一个数,在集合中都有唯一确定的数和它对应,那么就称为从集合到集合的一个函数,记作.
其中叫自变量,取值范围叫做函数的定义域;与的值相对应的值叫做函数值,函数值的集合叫做函数的值域.显然值域是集合的子集.
2.区间
设是两个实数,而且,我们规定:
(1)满足不等式的实数的集合叫做闭区间,表示为;
(2)满足不等式的实数的集合叫做开区间,表示为;
(3)满足不等式或的实数的集合叫做半开半闭区间,分别表示为.
(4)满足,,,的实数的集合分别表示为,,,.
3.函数的表示法
(1)解析法:用数学式子来表示两个变量之间的对应关系,这种表示函数的方法叫做解析法.
(2)列表法:用列出表格来表示两个变量之间的对应关系,这种表示函数的方法叫做列表法.
(3)图象法:用图象来表示两个变量之间的对应关系,这种表示函数的方法叫做图象法.
易混易错点:
1.表示是的函数,与之间不是相乘的关系,符号“”表示对变量所施行的运算法则.
2.函数三要素:①函数的定义域;②函数的值域;③对应法则.
其中对应法则是核心,定义域和值域都必须是非空的数集.按照对应法则,与自变量所对应的函数值必须唯一.
易错小题考考你
题一
题面:设,求,.
题二
题面:已知两个变量与之间满足关系式,则是的函数吗?
金题精讲
题一
题面:下列说法中正确的是(
)
A.变量、满足,则是的函数
B.变量、满足,则是的函数
C.变量、满足,则是的函数
D.变量、满足,则是的函数
题二
题面:已知下列四组函数,其中表示同一函数的是(
).
A.
B.
C.
D.
题三
题面:已知
(1)求;
(2)若,求.
题四
题面:求下列函数的定义域
(); ();
(); ().
课后拓展练习
注:此部分为老师根据本讲课程内容为大家精选的课下拓展题目,故不在课堂中讲解,请同学们课下自己练习并对照详解进行自测.
题一
题面:下列各对函数中,是同一函数的一对是(
).
(A)与
(B)与
(C)与
(D)与
难度:容易题
题二
题面:求下列函数中自变量的取值范围:
(1);
(2).
难度:容易题
题三
题面:判断下列说法是否正确:
(1)长方形的宽一定时,面积是长的函数;
(2)等腰三角形的面积是底边长的函数;
(3)某人的身高是年龄的函数;
(4)关系式中的是的函数.
难度:中等题
题四
题面:已知函数
若,则
;若,则
;
.
难度:中等题
讲义参考答案
易错小题考考你
题一
答案:,
题二
答案:不是的函数.
金题精讲
题一
答案:D
题二
答案:B
题三
答案:(1);(2)
题四
答案:(1)(2)
(3)(4)
课后拓展练习
题一
答案:C.
详解:A选项中两个函数的值域不同,B选项中的两个函数的定义域不同,D选项中的两个函数的定义域也不同,故A、B、D都错误,因此选C.
题二
答案:(1)是;(2).
详解:(1)由得,所以的取值范围是.
(2)由得,所以的取值范围是.
题三
答案:(1)正确;(2)错误;(3)正确;(4)错误.
详解:(1)长方形的宽一定时,其长所取的每一个确定的值,面积都有唯一确定的值与它对应,所以面积是长的函数.
(2)因为三角形的面积受底和高两个因素的影响,当等腰三角形的底取一个定值时,它的面积还因受高的影响而不能有唯一确定的值和底的取值相对应,所以面积不是底边长函数.
(3)人的任意一个确定的年龄,都有唯一确定的身高与之对应,所以这个人的身高是年龄函数.
(4)当时,,此时,不唯一.所以不是的函数.
题四
答案:(1);(2);(3).
详解:当时,,则.
当时,,,
则,.
函数的概念及其表示法
学案
主要考点梳理
1.函数定义
设是非空数集,如果按照某个确定的对应关系,使对应集合中的任意一个数,在集合中都有唯一确定的数和它对应,那么就称为从集合到集合的一个函数,记作.
其中叫自变量,取值范围叫做函数的定义域;与的值相对应的值叫做函数值,函数值的集合叫做函数的值域.显然值域是集合的子集.
2.区间
设是两个实数,而且,我们规定:
(1)满足不等式的实数的集合叫做闭区间,表示为;
(2)满足不等式的实数的集合叫做开区间,表示为;
(3)满足不等式或的实数的集合叫做半开半闭区间,分别表示为.
(4)满足,,,的实数的集合分别表示为,,,.
3.函数的表示法
(1)解析法:用数学式子来表示两个变量之间的对应关系,这种表示函数的方法叫做解析法.
(2)列表法:用列出表格来表示两个变量之间的对应关系,这种表示函数的方法叫做列表法.
(3)图象法:用图象来表示两个变量之间的对应关系,这种表示函数的方法叫做图象法.
易混易错点:
1.表示是的函数,与之间不是相乘的关系,符号“”表示对变量所施行的运算法则.
2.函数三要素:①函数的定义域;②函数的值域;③对应法则.
其中对应法则是核心,定义域和值域都必须是非空的数集.按照对应法则,与自变量所对应的函数值必须唯一.
易错小题考考你
题一
题面:设,求,.
题二
题面:已知两个变量与之间满足关系式,则是的函数吗?
金题精讲
题一
题面:下列说法中正确的是(
)
A.变量、满足,则是的函数
B.变量、满足,则是的函数
C.变量、满足,则是的函数
D.变量、满足,则是的函数
题二
题面:已知下列四组函数,其中表示同一函数的是(
).
A.
B.
C.
D.
题三
题面:已知
(1)求;
(2)若,求.
题四
题面:求下列函数的定义域
(); ();
(); ().
课后拓展练习
注:此部分为老师根据本讲课程内容为大家精选的课下拓展题目,故不在课堂中讲解,请同学们课下自己练习并对照详解进行自测.
题一
题面:下列各对函数中,是同一函数的一对是(
).
(A)与
(B)与
(C)与
(D)与
难度:容易题
题二
题面:求下列函数中自变量的取值范围:
(1);
(2).
难度:容易题
题三
题面:判断下列说法是否正确:
(1)长方形的宽一定时,面积是长的函数;
(2)等腰三角形的面积是底边长的函数;
(3)某人的身高是年龄的函数;
(4)关系式中的是的函数.
难度:中等题
题四
题面:已知函数
若,则
;若,则
;
.
难度:中等题
讲义参考答案
易错小题考考你
题一
答案:,
题二
答案:不是的函数.
金题精讲
题一
答案:D
题二
答案:B
题三
答案:(1);(2)
题四
答案:(1)(2)
(3)(4)
课后拓展练习
题一
答案:C.
详解:A选项中两个函数的值域不同,B选项中的两个函数的定义域不同,D选项中的两个函数的定义域也不同,故A、B、D都错误,因此选C.
题二
答案:(1)是;(2).
详解:(1)由得,所以的取值范围是.
(2)由得,所以的取值范围是.
题三
答案:(1)正确;(2)错误;(3)正确;(4)错误.
详解:(1)长方形的宽一定时,其长所取的每一个确定的值,面积都有唯一确定的值与它对应,所以面积是长的函数.
(2)因为三角形的面积受底和高两个因素的影响,当等腰三角形的底取一个定值时,它的面积还因受高的影响而不能有唯一确定的值和底的取值相对应,所以面积不是底边长函数.
(3)人的任意一个确定的年龄,都有唯一确定的身高与之对应,所以这个人的身高是年龄函数.
(4)当时,,此时,不唯一.所以不是的函数.
题四
答案:(1);(2);(3).
详解:当时,,则.
当时,,,
则,.
