2.2.2 函数的表示法 同步测试(含答案)
文档属性
| 名称 | 2.2.2 函数的表示法 同步测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 97.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-13 00:00:00 | ||
图片预览

文档简介
2.2.2
函数的表示法
时间:45分钟 分值:100分
一、选择题(每小题6分,共计36分)
1.设f(x)=2x+3,g(x)=f(x-2),则g(x)等于( )
A.2x+1
B.2x-1
C.2x-3
D.2x+7
解析:∵f(x)=2x+3,∴f(x-2)=2(x-2)+3=2x-1,即g(x)=2x-1,故选B.
答案:B
2.已知f(x)是一次函数,且满足3f(x+1)=2x+17,则f(x)等于( )
A.x+5
B.x+1
C.2x-3
D.2x+1
解析:∵f(x)是一次函数,∴设f(x)=ax+b(a≠0),
由3f(x+1)=2x+17,得3[a(x+1)+b]=2x+17,
整理得:3ax+3(a+b)=2x+17,
∴∴故选A.
答案:A
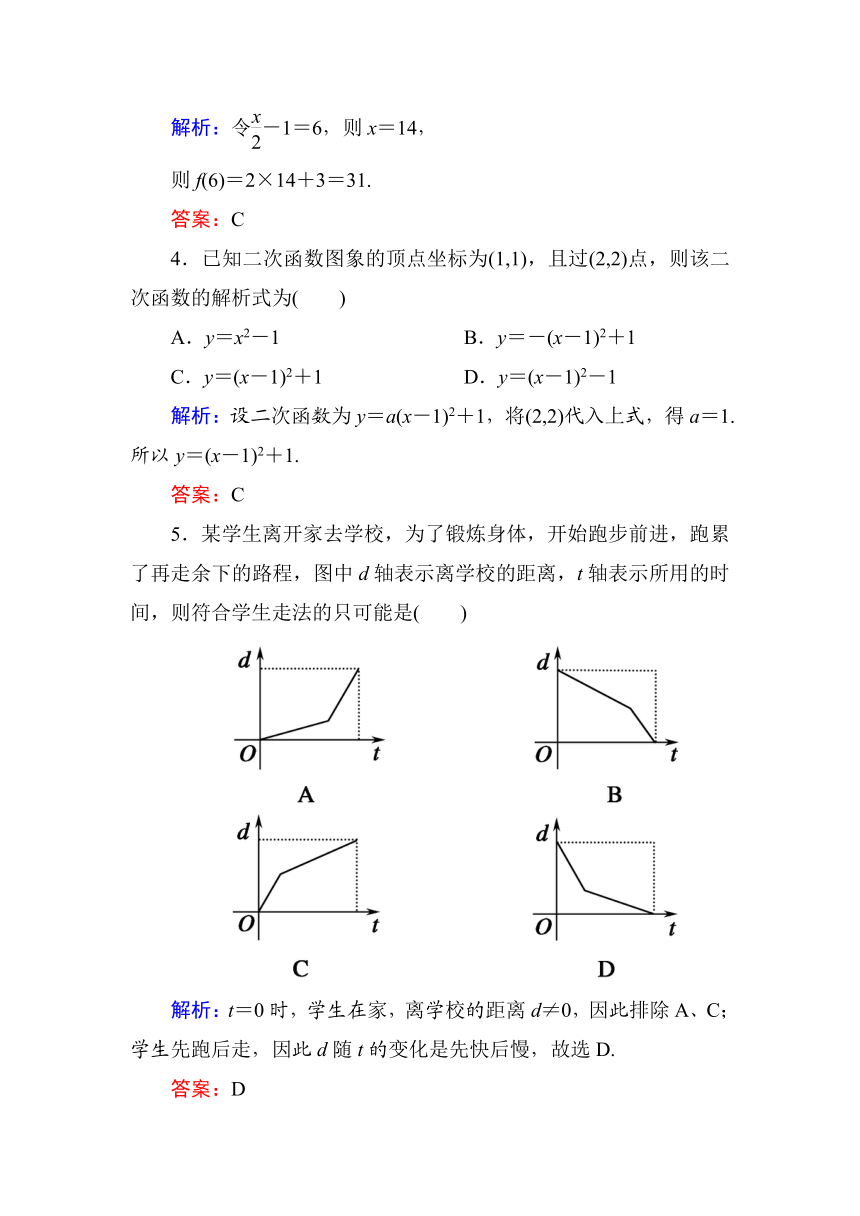
3.已知f=2x+3,则f(6)的值为( )
A.15
B.7
C.31
D.17
解析:令-1=6,则x=14,
则f(6)=2×14+3=31.
答案:C
4.已知二次函数图象的顶点坐标为(1,1),且过(2,2)点,则该二次函数的解析式为( )
A.y=x2-1
B.y=-(x-1)2+1
C.y=(x-1)2+1
D.y=(x-1)2-1
解析:设二次函数为y=a(x-1)2+1,将(2,2)代入上式,得a=1.所以y=(x-1)2+1.
答案:C
5.某学生离开家去学校,为了锻炼身体,开始跑步前进,跑累了再走余下的路程,图中d轴表示离学校的距离,t轴表示所用的时间,则符合学生走法的只可能是( )
解析:t=0时,学生在家,离学校的距离d≠0,因此排除A、C;学生先跑后走,因此d随t的变化是先快后慢,故选D.
答案:D
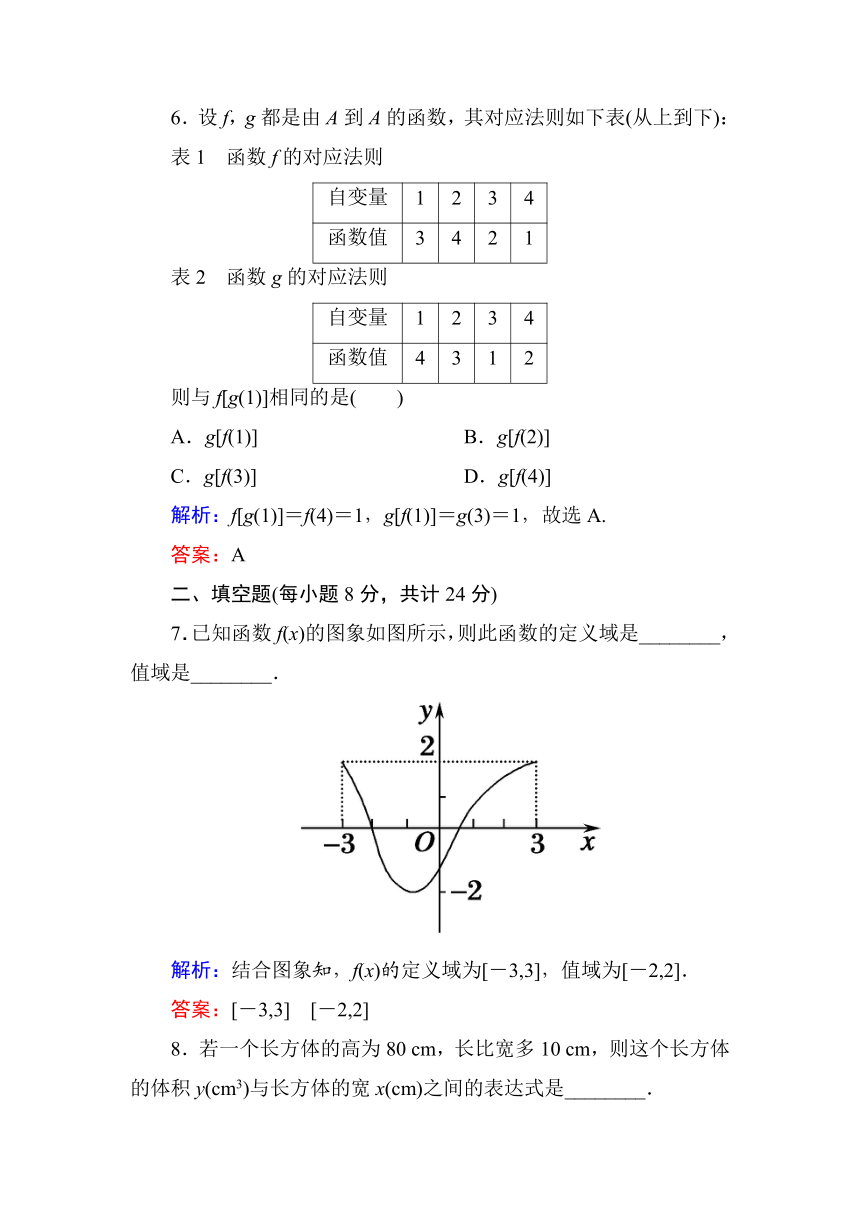
6.设f,g都是由A到A的函数,其对应法则如下表(从上到下):
表1 函数f的对应法则
自变量
1
2
3
4
函数值
3
4
2
1
表2 函数g的对应法则
自变量
1
2
3
4
函数值
4
3
1
2
则与f[g(1)]相同的是( )
A.g[f(1)]
B.g[f(2)]
C.g[f(3)]
D.g[f(4)]
解析:f[g(1)]=f(4)=1,g[f(1)]=g(3)=1,故选A.
答案:A
二、填空题(每小题8分,共计24分)
7.已知函数f(x)的图象如图所示,则此函数的定义域是________,值域是________.
解析:结合图象知,f(x)的定义域为[-3,3],值域为[-2,2].
答案:[-3,3] [-2,2]
8.若一个长方体的高为80
cm,长比宽多10
cm,则这个长方体的体积y(cm3)与长方体的宽x(cm)之间的表达式是________.
解析:y=(10+x)x·80=80x2+800x(x>0).
答案:y=80x2+800x(x>0)
9.已知函数f(x)对任意实数x,y均有f(xy)=f(x)+f(y),且f(2)=1,则f(1)=__________,f=__________.
解析:∵f(2)=f(2×1)=f(2)+f(1),∴f(1)=0.
又f(1)=f=f(2)+f=0,∴f=-1.
答案:0 -1
三、解答题(共计40分)
10.(10分)作出下列函数的图象.
(1)y=1-x,x∈Z;
(2)y=2x2-4x-3,0≤x<3.
解:
11.(15分)某商场新进了10台彩电,每台售价3
000元,试求售出台数x与收款数y之间的函数关系,分别用列表法、图象法、解析法表示出来.
解析:函数的定义域是{1,2,3,…,10},值域是{3
000,6
000,9
000,…,30
000},可直接列表、画图表示,分析题意得到表示y与x关系的解析式,注意定义域.
解:(1)列表法如下:
x(台)
1
2
3
4
5
y(元)
3
000
6
000
9
000
12
000
15
000
x(台)
6
7
8
9
10
y(元)
18
000
21
000
24
000
27
000
30
000
(2)图象法:如下图所示.
(3)解析法:y=3
000x,x∈{1,2,3,…,10}.
——能力提升——
12.(15分)已知函数f(x)对任意实数a,b,都有f(ab)=f(a)+f(b)成立.
(1)求f(0)与f(1)的值;
(2)求证:f()=-f(x);
(3)若f(2)=p,f(3)=q(p,q均为常数),求f(36)的值.
解:(1)令a=b=0,得f(0)=f(0)+f(0),解得f(0)=0;令a=1,b=0,得f(0)=f(1)+f(0),解得f(1)=0.
(2)证明:令a=,b=x,得f(1)=f()+f(x)=0,
∴f()=-f(x).
(3)令a=b=2,得f(4)=f(2)+f(2)=2p,
令a=b=3,得f(9)=f(3)+f(3)=2q.
令a=4,b=9,得f(36)=f(4)+f(9)=2p+2q.
函数的表示法
时间:45分钟 分值:100分
一、选择题(每小题6分,共计36分)
1.设f(x)=2x+3,g(x)=f(x-2),则g(x)等于( )
A.2x+1
B.2x-1
C.2x-3
D.2x+7
解析:∵f(x)=2x+3,∴f(x-2)=2(x-2)+3=2x-1,即g(x)=2x-1,故选B.
答案:B
2.已知f(x)是一次函数,且满足3f(x+1)=2x+17,则f(x)等于( )
A.x+5
B.x+1
C.2x-3
D.2x+1
解析:∵f(x)是一次函数,∴设f(x)=ax+b(a≠0),
由3f(x+1)=2x+17,得3[a(x+1)+b]=2x+17,
整理得:3ax+3(a+b)=2x+17,
∴∴故选A.
答案:A
3.已知f=2x+3,则f(6)的值为( )
A.15
B.7
C.31
D.17
解析:令-1=6,则x=14,
则f(6)=2×14+3=31.
答案:C
4.已知二次函数图象的顶点坐标为(1,1),且过(2,2)点,则该二次函数的解析式为( )
A.y=x2-1
B.y=-(x-1)2+1
C.y=(x-1)2+1
D.y=(x-1)2-1
解析:设二次函数为y=a(x-1)2+1,将(2,2)代入上式,得a=1.所以y=(x-1)2+1.
答案:C
5.某学生离开家去学校,为了锻炼身体,开始跑步前进,跑累了再走余下的路程,图中d轴表示离学校的距离,t轴表示所用的时间,则符合学生走法的只可能是( )
解析:t=0时,学生在家,离学校的距离d≠0,因此排除A、C;学生先跑后走,因此d随t的变化是先快后慢,故选D.
答案:D
6.设f,g都是由A到A的函数,其对应法则如下表(从上到下):
表1 函数f的对应法则
自变量
1
2
3
4
函数值
3
4
2
1
表2 函数g的对应法则
自变量
1
2
3
4
函数值
4
3
1
2
则与f[g(1)]相同的是( )
A.g[f(1)]
B.g[f(2)]
C.g[f(3)]
D.g[f(4)]
解析:f[g(1)]=f(4)=1,g[f(1)]=g(3)=1,故选A.
答案:A
二、填空题(每小题8分,共计24分)
7.已知函数f(x)的图象如图所示,则此函数的定义域是________,值域是________.
解析:结合图象知,f(x)的定义域为[-3,3],值域为[-2,2].
答案:[-3,3] [-2,2]
8.若一个长方体的高为80
cm,长比宽多10
cm,则这个长方体的体积y(cm3)与长方体的宽x(cm)之间的表达式是________.
解析:y=(10+x)x·80=80x2+800x(x>0).
答案:y=80x2+800x(x>0)
9.已知函数f(x)对任意实数x,y均有f(xy)=f(x)+f(y),且f(2)=1,则f(1)=__________,f=__________.
解析:∵f(2)=f(2×1)=f(2)+f(1),∴f(1)=0.
又f(1)=f=f(2)+f=0,∴f=-1.
答案:0 -1
三、解答题(共计40分)
10.(10分)作出下列函数的图象.
(1)y=1-x,x∈Z;
(2)y=2x2-4x-3,0≤x<3.
解:
11.(15分)某商场新进了10台彩电,每台售价3
000元,试求售出台数x与收款数y之间的函数关系,分别用列表法、图象法、解析法表示出来.
解析:函数的定义域是{1,2,3,…,10},值域是{3
000,6
000,9
000,…,30
000},可直接列表、画图表示,分析题意得到表示y与x关系的解析式,注意定义域.
解:(1)列表法如下:
x(台)
1
2
3
4
5
y(元)
3
000
6
000
9
000
12
000
15
000
x(台)
6
7
8
9
10
y(元)
18
000
21
000
24
000
27
000
30
000
(2)图象法:如下图所示.
(3)解析法:y=3
000x,x∈{1,2,3,…,10}.
——能力提升——
12.(15分)已知函数f(x)对任意实数a,b,都有f(ab)=f(a)+f(b)成立.
(1)求f(0)与f(1)的值;
(2)求证:f()=-f(x);
(3)若f(2)=p,f(3)=q(p,q均为常数),求f(36)的值.
解:(1)令a=b=0,得f(0)=f(0)+f(0),解得f(0)=0;令a=1,b=0,得f(0)=f(1)+f(0),解得f(1)=0.
(2)证明:令a=,b=x,得f(1)=f()+f(x)=0,
∴f()=-f(x).
(3)令a=b=2,得f(4)=f(2)+f(2)=2p,
令a=b=3,得f(9)=f(3)+f(3)=2q.
令a=4,b=9,得f(36)=f(4)+f(9)=2p+2q.
