2.3 函数的单调性 教案1
图片预览

文档简介
2.3
函数的单调性
教案
教学目的:
(1)通过已学过的函数特别是二次函数,理解函数的单调性及其几何意义;
(2)学会运用函数图象理解和研究函数的性质;
(3)能够熟练应用定义判断数在某区间上的的单调性.
教学重点:函数的单调性及其几何意义.
教学难点:利用函数的单调性定义判断、证明函数的单调性.
教学过程:
阅读与思考
1、阅读教材
P36的实例分析及思考交流止。
2、思考问题
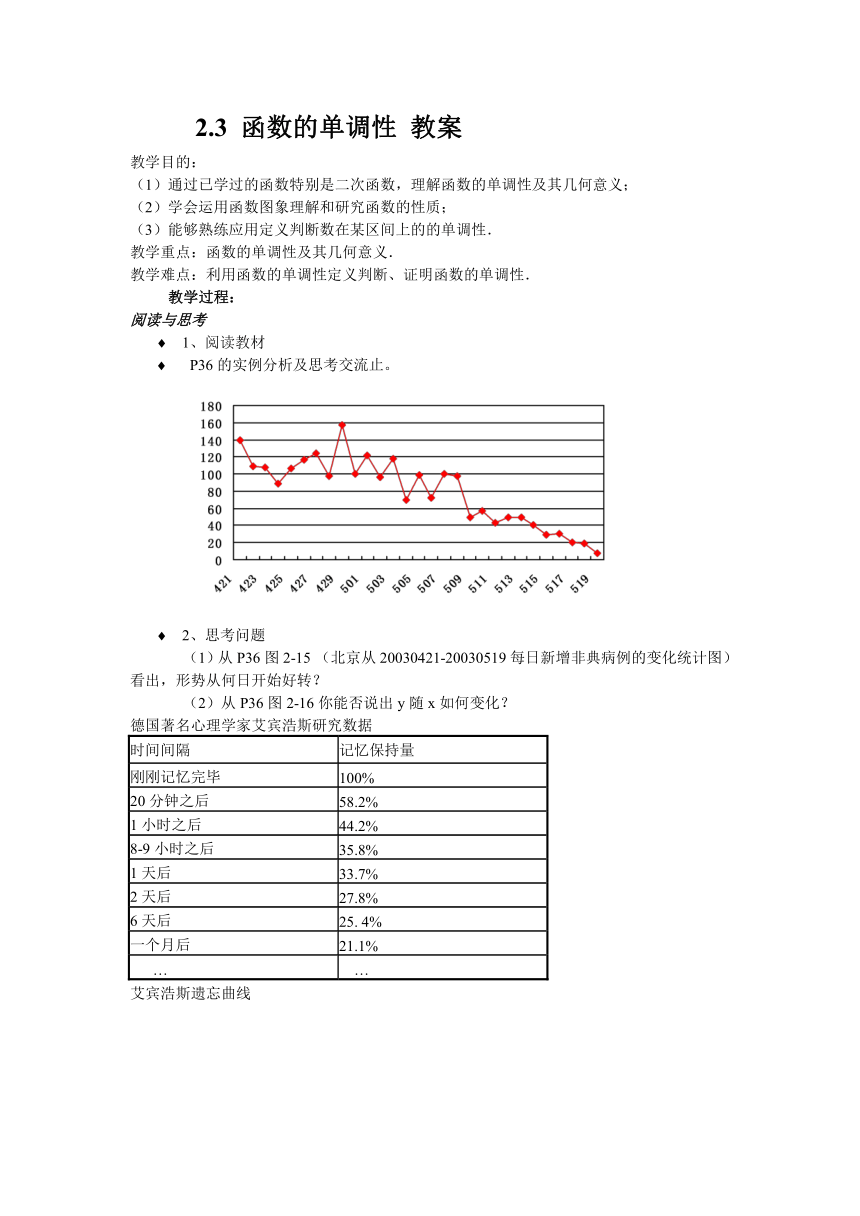
(1)从P36图2-15
(北京从20030421-20030519每日新增非典病例的变化统计图)看出,形势从何日开始好转?
(2)从P36图2-16你能否说出y随x如何变化?
德国著名心理学家艾宾浩斯研究数据
时间间隔
记忆保持量
刚刚记忆完毕
100%
20分钟之后
58.2%
1小时之后
44.2%
8-9小时之后
35.8%
1天后
33.7%
2天后
27.8%
6天后
25.
4%
一个月后
21.1%
…
…
艾宾浩斯遗忘曲线
问:什么是增函数、减函数、函数的单调性?
问题1、
作出下列函数的图象,并指出图象的变化趋势:
问题2、你能明确地说出“图象呈逐渐上升或下降趋势”的意思吗?
在某一区间内,
图象在该区间呈上升趋势
当x的值增大时,函数值y也增大
图象在该区间呈下降趋势
当x的值增大时,函数值y反而减小
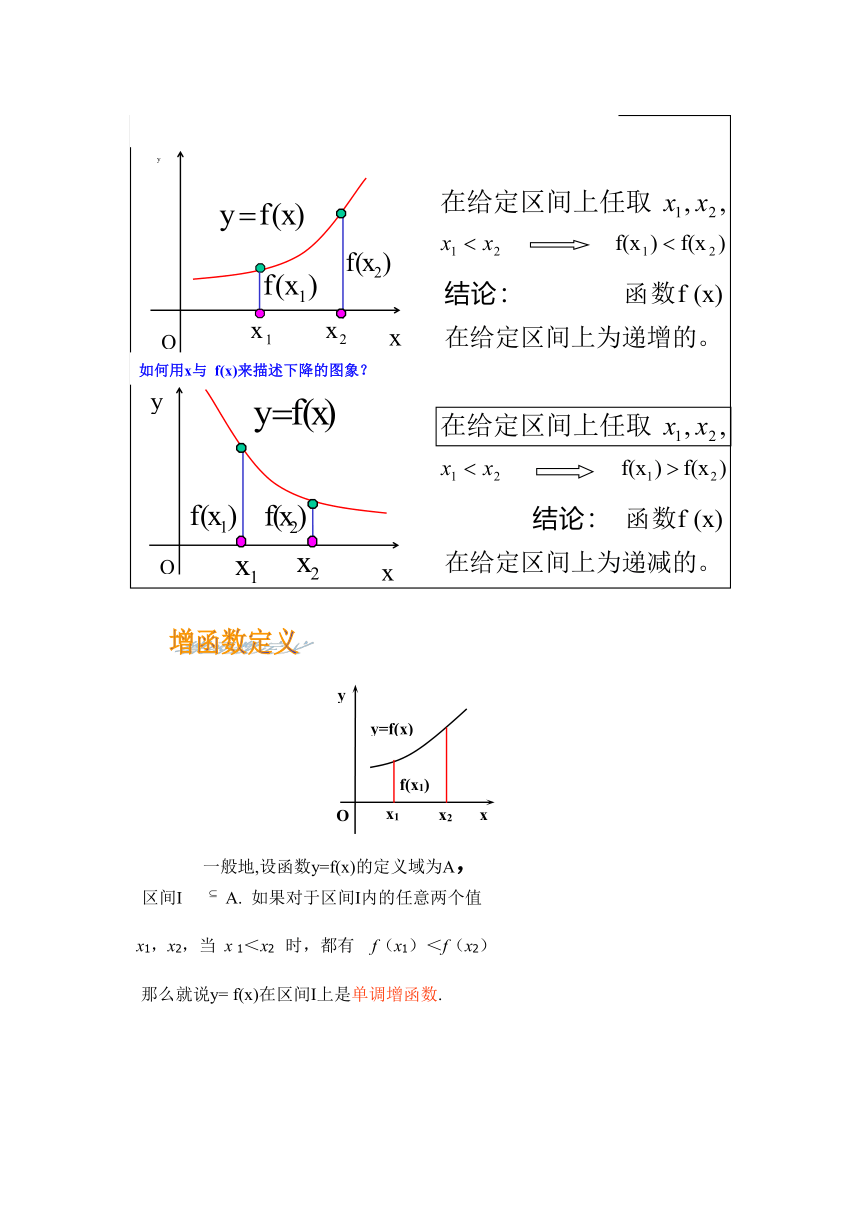
如何用x与
f
(x)来描述上升的图象?
单调区间
如果函数y=f(x)在区间I是单调增函数或单调减函数,那么就说函数y=f(x)在区间I上具有单调性.
单调增区间和单调减区间统称为单调区间.
小结
版权所有:高考资源网(www.k
s
5
u.com)
保持量(百分数)
天数
1
2
3
4
5
6
0
20
40
60
80
100
O
x
y
y
O
x
O
x
y
-1
y
O
x
结论:
函数f
(x)在给定区间上为递增的。
O
x
y
如何用x与
f(x)来描述下降的图象?
结论:
函数f
(x)在给定区间上为递减的。
O
x
y
x
y
O
y=f(x)
x1
x2
f(x1)
f(x2)
那么就说y=
f(x)在区间I上是单调增函数.
一般地,设函数y=f(x)的定义域为A,
区间I
A.
如果对于区间I内的任意两个值
x1,x2,当
x
1<x2
时,都有
f(x1)<f(x2)
x
y
O
y=f(x)
x1
x2
f(x1)
f(x2)
那么就说y=
f(x)在区间I上是单调增函数.
一般地,设函数y=f(x)的定义域为A,
区间I
A.
如果对于区间I内的任意两个值
x1,x2,当
x
1<x2
时,都有
f(x1)<f(x2)
证明:
(条件)
(论证结果)
(结论)
单调递增区间:
单调递减区间:
x
y
2
1
o
【练习】:
1、判断函数f(x)=1/x在(-∞,0)上是增函数还是减函数?并证明你的结论.
【想一想】:能否说函数f(x)=1/x在(-∞,+∞)
上是减函数?
答:
不能.
因为x=0不属于f(x)=1/x的定义域.
减函数
2、判断函数f(x)=1/x在(0,+∞)上
是增函数还是减函数?并证明你的结论.
减函数
解题步骤
用定义证明函数的单调性的步骤:
(1).
设x1<x2,
并且是某个区间上任意二个值;
(2).
作差
f(x1)-f(x2)
;
(3).
判断
f(x1)-f(x2)
的符号:
(4).
作结论.
①
分解因式,
得出因式x1-x2
.
②
配成非负实数和.
1.
概念
2.
方法
定义法
图象法
函数的单调性
教案
教学目的:
(1)通过已学过的函数特别是二次函数,理解函数的单调性及其几何意义;
(2)学会运用函数图象理解和研究函数的性质;
(3)能够熟练应用定义判断数在某区间上的的单调性.
教学重点:函数的单调性及其几何意义.
教学难点:利用函数的单调性定义判断、证明函数的单调性.
教学过程:
阅读与思考
1、阅读教材
P36的实例分析及思考交流止。
2、思考问题
(1)从P36图2-15
(北京从20030421-20030519每日新增非典病例的变化统计图)看出,形势从何日开始好转?
(2)从P36图2-16你能否说出y随x如何变化?
德国著名心理学家艾宾浩斯研究数据
时间间隔
记忆保持量
刚刚记忆完毕
100%
20分钟之后
58.2%
1小时之后
44.2%
8-9小时之后
35.8%
1天后
33.7%
2天后
27.8%
6天后
25.
4%
一个月后
21.1%
…
…
艾宾浩斯遗忘曲线
问:什么是增函数、减函数、函数的单调性?
问题1、
作出下列函数的图象,并指出图象的变化趋势:
问题2、你能明确地说出“图象呈逐渐上升或下降趋势”的意思吗?
在某一区间内,
图象在该区间呈上升趋势
当x的值增大时,函数值y也增大
图象在该区间呈下降趋势
当x的值增大时,函数值y反而减小
如何用x与
f
(x)来描述上升的图象?
单调区间
如果函数y=f(x)在区间I是单调增函数或单调减函数,那么就说函数y=f(x)在区间I上具有单调性.
单调增区间和单调减区间统称为单调区间.
小结
版权所有:高考资源网(www.k
s
5
u.com)
保持量(百分数)
天数
1
2
3
4
5
6
0
20
40
60
80
100
O
x
y
y
O
x
O
x
y
-1
y
O
x
结论:
函数f
(x)在给定区间上为递增的。
O
x
y
如何用x与
f(x)来描述下降的图象?
结论:
函数f
(x)在给定区间上为递减的。
O
x
y
x
y
O
y=f(x)
x1
x2
f(x1)
f(x2)
那么就说y=
f(x)在区间I上是单调增函数.
一般地,设函数y=f(x)的定义域为A,
区间I
A.
如果对于区间I内的任意两个值
x1,x2,当
x
1<x2
时,都有
f(x1)<f(x2)
x
y
O
y=f(x)
x1
x2
f(x1)
f(x2)
那么就说y=
f(x)在区间I上是单调增函数.
一般地,设函数y=f(x)的定义域为A,
区间I
A.
如果对于区间I内的任意两个值
x1,x2,当
x
1<x2
时,都有
f(x1)<f(x2)
证明:
(条件)
(论证结果)
(结论)
单调递增区间:
单调递减区间:
x
y
2
1
o
【练习】:
1、判断函数f(x)=1/x在(-∞,0)上是增函数还是减函数?并证明你的结论.
【想一想】:能否说函数f(x)=1/x在(-∞,+∞)
上是减函数?
答:
不能.
因为x=0不属于f(x)=1/x的定义域.
减函数
2、判断函数f(x)=1/x在(0,+∞)上
是增函数还是减函数?并证明你的结论.
减函数
解题步骤
用定义证明函数的单调性的步骤:
(1).
设x1<x2,
并且是某个区间上任意二个值;
(2).
作差
f(x1)-f(x2)
;
(3).
判断
f(x1)-f(x2)
的符号:
(4).
作结论.
①
分解因式,
得出因式x1-x2
.
②
配成非负实数和.
1.
概念
2.
方法
定义法
图象法
