2.3.1 函数的单调性与最大(小)值(1) 学案1(含答案)
文档属性
| 名称 | 2.3.1 函数的单调性与最大(小)值(1) 学案1(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 90.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-14 14:27:10 | ||
图片预览

文档简介
2.3.1函数的单调性与最大(小)值(1)学案
课前预习学案
一、预习目标:
1.
通过已学过的函数特别是二次函数,理解函数的单调性及其几何意义;
2.熟记函数单调性的定义
二、预习内容:
1.
观察下列各个函数的图象,并说说它们分别反映了相应函数的哪些变化规律:
随x的增大,y的值有什么变化?
能否看出函数的最大、最小值?
函数图象是否具有某种对称性?
2.画出下列函数的图象,观察其变化规律:
(1)f(x)
=
x
从左至右图象上升还是下降
______
在区间
____________
上,随着x的增
大,f(x)的值随着
________
.
(2)f(x)
=
-x+2
从左至右图象上升还是下降
______
在区间
____________
上,随着x的增
大,f(x)的值随着
________
.
(3)f(x)
=
x2
在区间
____________
上,
f(x)的值随着x的增大而
________
.
在区间
____________
上,f(x)的值随
着x的增大而
________
.
3.一般地,设函数y=f(x)的定义域为I,
如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,
(1)当x1f(x2),那么就说f(x)在区间D上是
函数
(2)当x1f(x2),那么就说f(x)在区间D上是
函数
三、提出疑惑
同学们,通过你的自主学习,你还有哪些疑惑,请把它填在下面的表格中
疑惑点
疑惑内容
课内探究学案
一、学习目标
1.
通过已学过的函数特别是二次函数,理解函数的单调性及其几何意义;
2.
学会运用函数图象理解和研究函数的性质;
3.
能够熟练应用定义判断与证明函数在某区间上的单调性.
学习重点:函数的单调性及其几何意义.
学习难点:利用函数的单调性定义判断、证明函数的单调性
二、学习过程
例1
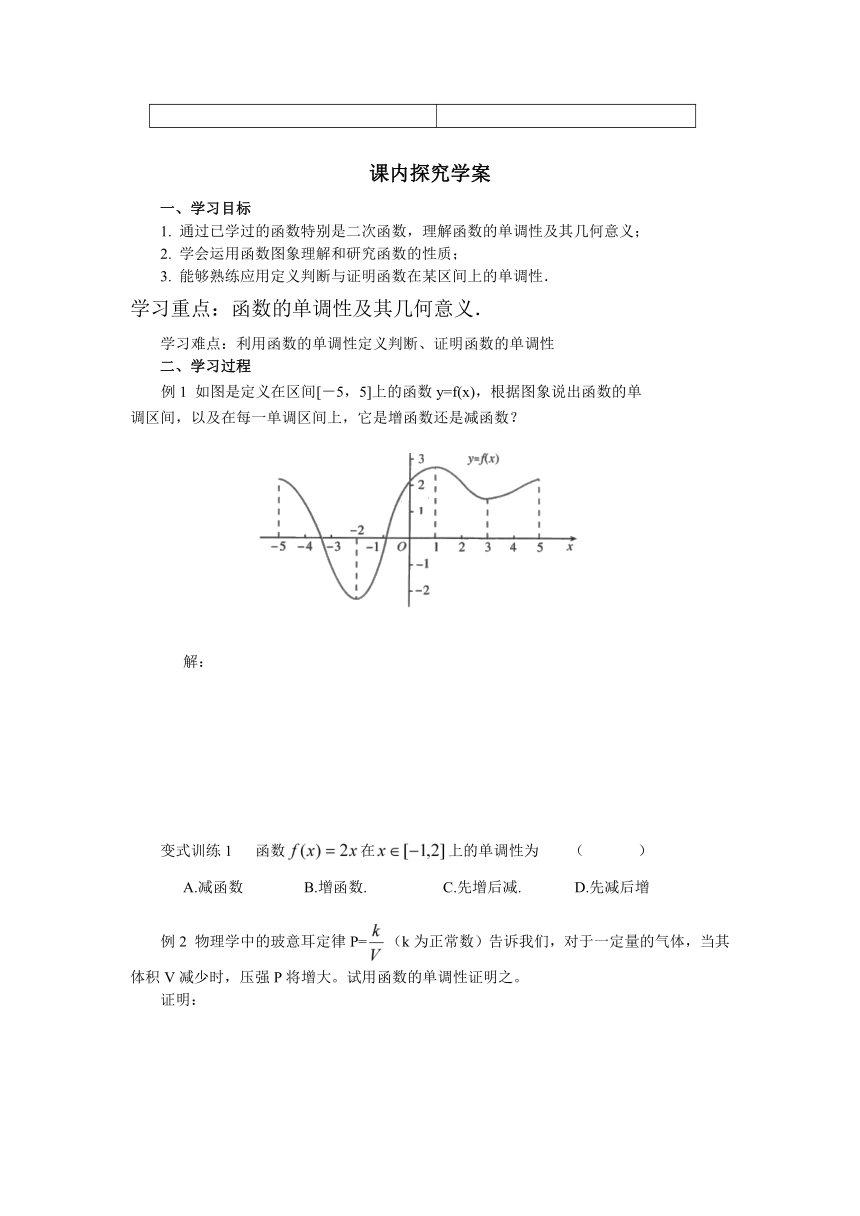
如图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单
调区间,以及在每一单调区间上,它是增函数还是减函数?
解:
变式训练1
函数在上的单调性为
(
)
A.减函数
B.增函数.
C.先增后减.
D.先减后增
例2
物理学中的玻意耳定律P=(k为正常数)告诉我们,对于一定量的气体,当其体积V减少时,压强P将增大。试用函数的单调性证明之。
证明:
变式训练2
若函数在上是增函数,那么
(
)
A.b>0
B.
b<0
C.m>0
D.m<0
例3.证明函数在(1,+∞)上为增函数
解:
变式训练3.:画出反比例函数的图象.
这个函数的定义域是什么?
它在定义域I上的单调性怎样?证明你的结论.
三、当堂检测
1、函数的单调增区间为
(
)
A.
B.
C.
D.
2、函数,当时是增函数,当时是减函数,则等于
(
)
A.-3
B.13
C.7
D.由m而定的常数
3、若函数在上是减函数,则的取值范围是
(
)
A.
B.
C.
D.
4、函数的减区间是____________________.
5、若函数在上是减函数,则的取值范围是______.
课后练习与提高
选择题
1、下列函数中,在区间(0,2)上为增函数的是
(
)
A.
B.
C.
D.
2、函数的单调减区间是
(
)
A.
B.
C.
D.
二、填空题:
3、函数,上的单调性是_____________________.
4、已知函数在上递增,那么的取值范围是________.
三、解答题:
5、设函数为R上的增函数,令
(1)、求证:在R上为增函数
(2)、若,求证
参考答案
例一
略
变式训练一B
例二
略
变式训练二C
例三
解:设则
变式训练三略
版权所有:高考资源网(www.k
s
5
u.com)
y
x
1
-1
1
-1
y
x
1
-1
1
-1
y
x
1
-1
1
-1
y
x
1
-1
1
-1
y
x
1
-1
1
-1
y
x
1
-1
1
-1
课前预习学案
一、预习目标:
1.
通过已学过的函数特别是二次函数,理解函数的单调性及其几何意义;
2.熟记函数单调性的定义
二、预习内容:
1.
观察下列各个函数的图象,并说说它们分别反映了相应函数的哪些变化规律:
随x的增大,y的值有什么变化?
能否看出函数的最大、最小值?
函数图象是否具有某种对称性?
2.画出下列函数的图象,观察其变化规律:
(1)f(x)
=
x
从左至右图象上升还是下降
______
在区间
____________
上,随着x的增
大,f(x)的值随着
________
.
(2)f(x)
=
-x+2
从左至右图象上升还是下降
______
在区间
____________
上,随着x的增
大,f(x)的值随着
________
.
(3)f(x)
=
x2
在区间
____________
上,
f(x)的值随着x的增大而
________
.
在区间
____________
上,f(x)的值随
着x的增大而
________
.
3.一般地,设函数y=f(x)的定义域为I,
如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,
(1)当x1
函数
(2)当x1
函数
三、提出疑惑
同学们,通过你的自主学习,你还有哪些疑惑,请把它填在下面的表格中
疑惑点
疑惑内容
课内探究学案
一、学习目标
1.
通过已学过的函数特别是二次函数,理解函数的单调性及其几何意义;
2.
学会运用函数图象理解和研究函数的性质;
3.
能够熟练应用定义判断与证明函数在某区间上的单调性.
学习重点:函数的单调性及其几何意义.
学习难点:利用函数的单调性定义判断、证明函数的单调性
二、学习过程
例1
如图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单
调区间,以及在每一单调区间上,它是增函数还是减函数?
解:
变式训练1
函数在上的单调性为
(
)
A.减函数
B.增函数.
C.先增后减.
D.先减后增
例2
物理学中的玻意耳定律P=(k为正常数)告诉我们,对于一定量的气体,当其体积V减少时,压强P将增大。试用函数的单调性证明之。
证明:
变式训练2
若函数在上是增函数,那么
(
)
A.b>0
B.
b<0
C.m>0
D.m<0
例3.证明函数在(1,+∞)上为增函数
解:
变式训练3.:画出反比例函数的图象.
这个函数的定义域是什么?
它在定义域I上的单调性怎样?证明你的结论.
三、当堂检测
1、函数的单调增区间为
(
)
A.
B.
C.
D.
2、函数,当时是增函数,当时是减函数,则等于
(
)
A.-3
B.13
C.7
D.由m而定的常数
3、若函数在上是减函数,则的取值范围是
(
)
A.
B.
C.
D.
4、函数的减区间是____________________.
5、若函数在上是减函数,则的取值范围是______.
课后练习与提高
选择题
1、下列函数中,在区间(0,2)上为增函数的是
(
)
A.
B.
C.
D.
2、函数的单调减区间是
(
)
A.
B.
C.
D.
二、填空题:
3、函数,上的单调性是_____________________.
4、已知函数在上递增,那么的取值范围是________.
三、解答题:
5、设函数为R上的增函数,令
(1)、求证:在R上为增函数
(2)、若,求证
参考答案
例一
略
变式训练一B
例二
略
变式训练二C
例三
解:设则
变式训练三略
版权所有:高考资源网(www.k
s
5
u.com)
y
x
1
-1
1
-1
y
x
1
-1
1
-1
y
x
1
-1
1
-1
y
x
1
-1
1
-1
y
x
1
-1
1
-1
y
x
1
-1
1
-1
