2.4.1 二次函数的图像 教案1(含试题和答案)
文档属性
| 名称 | 2.4.1 二次函数的图像 教案1(含试题和答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 172.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-14 00:00:00 | ||
图片预览



文档简介
2.4.1二次函数的图像
教案
一.
教学内容:
二次函数的图像
二.
教学要求:
1.
掌握二次函数的对称性、单调性、最值公式及图象。理解并掌握二次函数、二次方程与二次不等式的内在联系,能利用“数形结合”,“判别式”和“韦达定理”讨论二次方程根的情况及二次不等式的解集。
2.
理解分数指数的概念,掌握有理指数幂的运算性质;理解对数的概念,掌握对数的运算性质。
3.
掌握指数与对数函数的概念,图象和性质,会用定义法证明指数函数与对数函数的单调性,能应用其性质解(证)相关问题。
三.
知识串讲
(一)二次函数
1.
形如f(x)=ax2+bx+c(a≠0)的函数叫做二次函数。
(1)二次函数的解析式
(2)图象和性质
2.
二次函数、二次方程与二次不等式
如下图:
3.
二次函数在闭区间上必有最大、最小值,它们只能在区间端点或顶点处取得。
4.
一元二次方程ax2+bx+c=0(a≠0)实根的分布
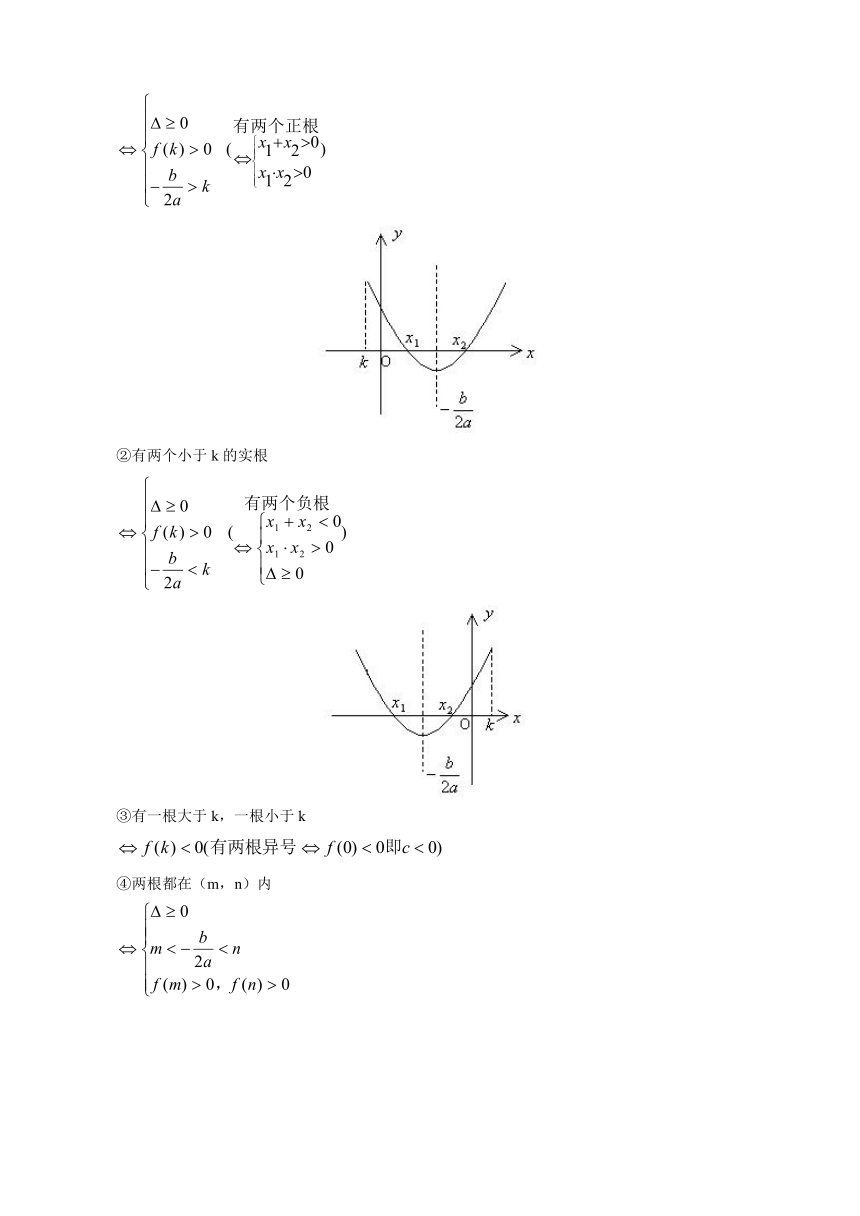
①有两个大于k的实根
②有两个小于k的实根
③有一根大于k,一根小于k
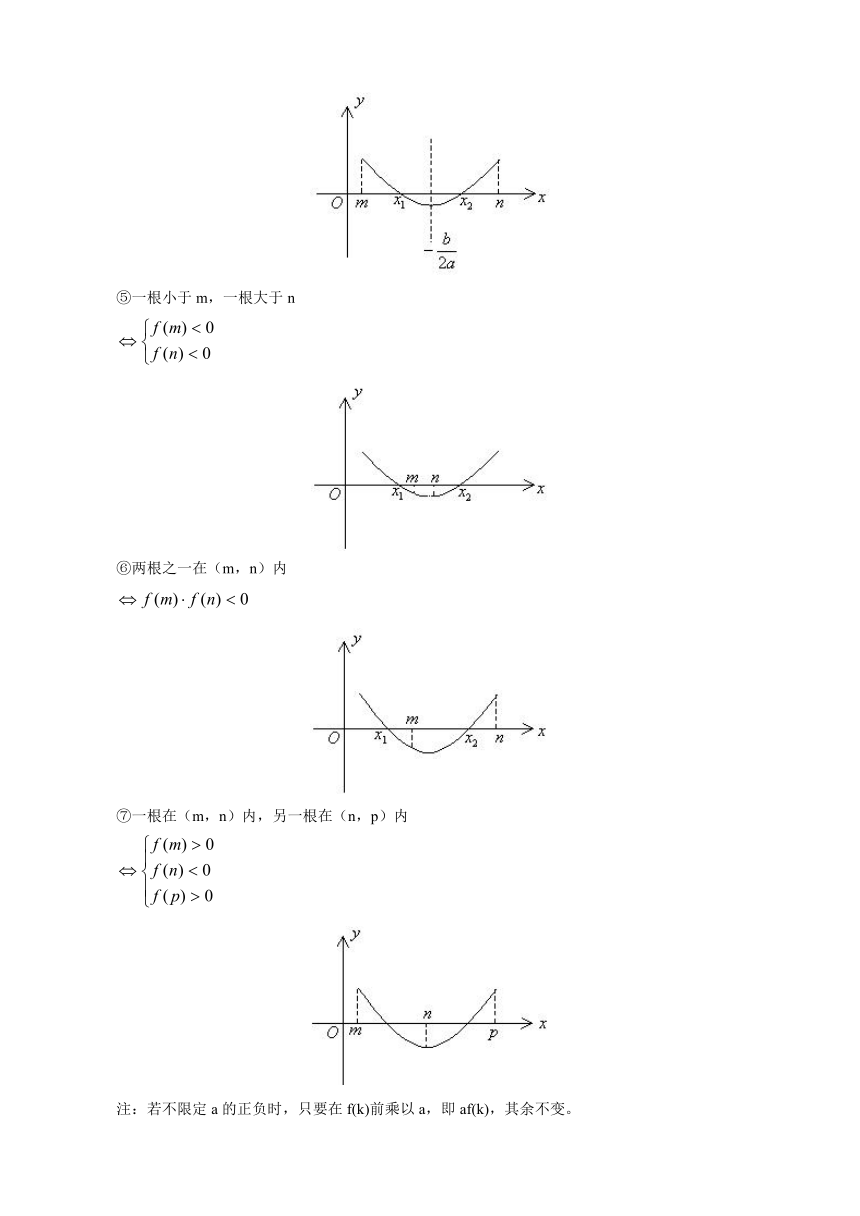
④两根都在(m,n)内
⑤一根小于m,一根大于n
⑥两根之一在(m,n)内
⑦一根在(m,n)内,另一根在(n,p)内
注:若不限定a的正负时,只要在f(k)前乘以a,即af(k),其余不变。
(二)指数与对数函数
1.
n次方根:若xn=a(n∈N,n>1),则称x为a的n次方程。
性质:
2.
指数
运算法则:
3.
对数
性质:
(1)0和负数没有对数,即N>0
运算法则:(M>0,N>0)
换底公式:
4.
指数函数与对数函数
图象过点(0,1),以x轴
图象过点(1,0),以y轴
为渐近线
为渐近线
底数互为倒数时,图象关于
底数互为倒数时,图象关于x轴
y轴对称,x>0时,“底大图高”
对称,x>1时“底大图低”
【典型例题】
例1.
设二次函数y=f(x)的最小值等于4,且f(0)=f(2)=6,求f(x)的解析式。
解法一:
解法二:
∴抛物线有对称轴x=1
又二次函数有最小值4
代入点(0,6)坐标,得a=2
例2.
若方程x2-11x+(30+a)=0的两根不等且均大于5,求实数a的取值范围。
解:(法一):
(法二):
例3.
设集合A={(x,y)|y=x2+ax+2},B={(x,y)|y=x+1,0≤x≤2},A∩B≠φ,求实数a的取值范围。
解:(分析:集合的元素是曲线上的点(x,y),A∩B≠φ,即曲线与线段有交点)
点评:对于方程x2+(a-1)x+1=0在[0,2]上有实根的问题,可考虑分离参数的方法,得到
例4.
函数f(x)=-x2+2ax+1-a在区间[0,1]上有最大值2,求实数a的值。
解:
抛物线的对称轴为x=a
(区间定,轴动的问题,根据对称轴的位置讨论)
(1)当x=a<0时,y在[0,1]上为减函数
(2)当0≤a≤1时
(3)当x=a>1时,y在[0,1]上为增函数
综上,a=-1或a=2
考虑:f(x)=x2+2x-1在区间[t,t+1]上的最小值是g(t)。
(3)则g(t)=?并求g(t)的最值,是区间动,轴定的问题。
例5.
已知函数y=a|x|(a>0且a≠1)的图象如图,则函数的图象是(
)
分析:由图象可知a>1
例6.
则f(x)的表达式为___________________
解:设x<0,则-x>0
又f(x)为奇函数
注:
例7.
(1)求f(x)的定义域;
(2)讨论f(x)的单调性;
(3)当a取何值时图象在y轴左侧;
解:
例8.
解:
(2)由于f(1)=2,由已知,得
例9.
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点,已知函数f(x)=ax2+(b+1)x+(b-1)(a≠0)
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动
解:
解得0(3)由题意,A、B两点应在直线y=x上
设A(x1,x1),B(x2,x2)
设AB的中点,为M(x’,y’)
点评:本题主要考查二次函数及其图象,一元二次方程以及不等式的综合应用,同时借助于不变量思想,以不动点为载体,蕴含着“及时定义→及时解答”的试题结构特征,对思维能力有较高要求。
【模拟试题】
一.
选择题
1.
已知函数的图象,如图,则m的取值范围是(
)
A.
B.
C.
D.
2.
已知函数,如果a>b>c且,则它的图象可能是(
)
3.
如果二次函数对任意实数x都有,那么(
)
A.
B.
C.
D.
4.
函数在区间[0,m]上有最大值3,最小值2,则m的取值范围是(
)
A.
B.
[0,2]
C.
D.
[1,2]
5.
设x1,x2是方程()的两个实根,则的最小值是(
)
A.
-2
B.
0
C.
1
D.
2
6.
若方程两根异号,则(
)
A.
B.
C.
D.
7.
如图是指数函数①;②;③;④的图象,则a,b,c,d的大小关系是(
)
A.
B.
C.
D.
8.
若,则a,b,c的大小关系是(
)
A.
aB.
bC.
aD.
b9.
当a>1时,在同一坐标系中,函数与的图象是(
)
10.
已知函数的定义域是[1,2],则函数的定义域是(
)
A.
[2,4]
B.
[4,16]
C.
[0,1]
D.
[1,2]
11.
已知函数,且g(x)的图象与f(x)的图象关于直线对称,则是(
)
A.
奇函数,且在(0,)上递减
B.
偶函数,且在(0,)上递增
C.
奇函数,且在(,0)上递减
D.
偶函数,且在(,0)上递增
二.
填空题
12.已知,当时,恒有,则m的取值范围是________________
(提示:①;②)
13.
求值
(1)_________
(2)_________
(3)_________
(4)已知,则_________
14.
函数是减函数,则a的取值范围是_________
15.
若,则a的取值范围是_________
16.
函数的单调递增区间是_________;单调递减区间是_________;值域是_________
三.
解答题
17.
已知在区间(,0)上是减函数,求f(x)的增区间。
解:设
在(,0)上
在上,
在上,____________________
在上,____________________
递增区间为:_______________
18.
已知常数a>1,变量x,y有关系:
(1)若,试以a,t表示y;
(2)若t在[1,)内变化时,y有最小值8,求此时a和x的值各为多少?
19.
对于函数,若存在,使成立,则称点(x0,x0)为函数的不动点
(1)已知函数有不动点(1,1)和(-3,-3),求a,b的值。
(2)若对于任意实数b,函数总有两个相异的不动点,求实数a的取值范围。
(3)若定义在实数集R上的奇函数存(有限的)n个不动点,求证n必为奇数。
【试题答案】
1.
B
2.
D
3.
C
4.
D
5.
C
6.
A
7.
B
8.
C
9.
B
10.
B
11.
D
12.
或
13.
(1);(2);(3)21;(4)
14.
15.
16.
,,
17.
,又;;
18.
解:(1)将代入原式,整理得
(2),
取最小值时,y取最小值
时,
由题意,得
19.
解:(1)由不动点定义有
把x=1代入得a=1,把a=1,x=-3代入得b=3
(2)与例9(2)相同,0(3)证明:是R上的奇函数,
,是的一个不动点
若有异于(0,0)点的不动点(x0,x0),则
又,也是的不动点
的有限个不动点除原点处,都是成对出现的,有2k个,加上原点,共有n=2k+1个,∴n为奇数
教案
一.
教学内容:
二次函数的图像
二.
教学要求:
1.
掌握二次函数的对称性、单调性、最值公式及图象。理解并掌握二次函数、二次方程与二次不等式的内在联系,能利用“数形结合”,“判别式”和“韦达定理”讨论二次方程根的情况及二次不等式的解集。
2.
理解分数指数的概念,掌握有理指数幂的运算性质;理解对数的概念,掌握对数的运算性质。
3.
掌握指数与对数函数的概念,图象和性质,会用定义法证明指数函数与对数函数的单调性,能应用其性质解(证)相关问题。
三.
知识串讲
(一)二次函数
1.
形如f(x)=ax2+bx+c(a≠0)的函数叫做二次函数。
(1)二次函数的解析式
(2)图象和性质
2.
二次函数、二次方程与二次不等式
如下图:
3.
二次函数在闭区间上必有最大、最小值,它们只能在区间端点或顶点处取得。
4.
一元二次方程ax2+bx+c=0(a≠0)实根的分布
①有两个大于k的实根
②有两个小于k的实根
③有一根大于k,一根小于k
④两根都在(m,n)内
⑤一根小于m,一根大于n
⑥两根之一在(m,n)内
⑦一根在(m,n)内,另一根在(n,p)内
注:若不限定a的正负时,只要在f(k)前乘以a,即af(k),其余不变。
(二)指数与对数函数
1.
n次方根:若xn=a(n∈N,n>1),则称x为a的n次方程。
性质:
2.
指数
运算法则:
3.
对数
性质:
(1)0和负数没有对数,即N>0
运算法则:(M>0,N>0)
换底公式:
4.
指数函数与对数函数
图象过点(0,1),以x轴
图象过点(1,0),以y轴
为渐近线
为渐近线
底数互为倒数时,图象关于
底数互为倒数时,图象关于x轴
y轴对称,x>0时,“底大图高”
对称,x>1时“底大图低”
【典型例题】
例1.
设二次函数y=f(x)的最小值等于4,且f(0)=f(2)=6,求f(x)的解析式。
解法一:
解法二:
∴抛物线有对称轴x=1
又二次函数有最小值4
代入点(0,6)坐标,得a=2
例2.
若方程x2-11x+(30+a)=0的两根不等且均大于5,求实数a的取值范围。
解:(法一):
(法二):
例3.
设集合A={(x,y)|y=x2+ax+2},B={(x,y)|y=x+1,0≤x≤2},A∩B≠φ,求实数a的取值范围。
解:(分析:集合的元素是曲线上的点(x,y),A∩B≠φ,即曲线与线段有交点)
点评:对于方程x2+(a-1)x+1=0在[0,2]上有实根的问题,可考虑分离参数的方法,得到
例4.
函数f(x)=-x2+2ax+1-a在区间[0,1]上有最大值2,求实数a的值。
解:
抛物线的对称轴为x=a
(区间定,轴动的问题,根据对称轴的位置讨论)
(1)当x=a<0时,y在[0,1]上为减函数
(2)当0≤a≤1时
(3)当x=a>1时,y在[0,1]上为增函数
综上,a=-1或a=2
考虑:f(x)=x2+2x-1在区间[t,t+1]上的最小值是g(t)。
(3)则g(t)=?并求g(t)的最值,是区间动,轴定的问题。
例5.
已知函数y=a|x|(a>0且a≠1)的图象如图,则函数的图象是(
)
分析:由图象可知a>1
例6.
则f(x)的表达式为___________________
解:设x<0,则-x>0
又f(x)为奇函数
注:
例7.
(1)求f(x)的定义域;
(2)讨论f(x)的单调性;
(3)当a取何值时图象在y轴左侧;
解:
例8.
解:
(2)由于f(1)=2,由已知,得
例9.
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点,已知函数f(x)=ax2+(b+1)x+(b-1)(a≠0)
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动
解:
解得0
设A(x1,x1),B(x2,x2)
设AB的中点,为M(x’,y’)
点评:本题主要考查二次函数及其图象,一元二次方程以及不等式的综合应用,同时借助于不变量思想,以不动点为载体,蕴含着“及时定义→及时解答”的试题结构特征,对思维能力有较高要求。
【模拟试题】
一.
选择题
1.
已知函数的图象,如图,则m的取值范围是(
)
A.
B.
C.
D.
2.
已知函数,如果a>b>c且,则它的图象可能是(
)
3.
如果二次函数对任意实数x都有,那么(
)
A.
B.
C.
D.
4.
函数在区间[0,m]上有最大值3,最小值2,则m的取值范围是(
)
A.
B.
[0,2]
C.
D.
[1,2]
5.
设x1,x2是方程()的两个实根,则的最小值是(
)
A.
-2
B.
0
C.
1
D.
2
6.
若方程两根异号,则(
)
A.
B.
C.
D.
7.
如图是指数函数①;②;③;④的图象,则a,b,c,d的大小关系是(
)
A.
B.
C.
D.
8.
若,则a,b,c的大小关系是(
)
A.
a
b
a
b
当a>1时,在同一坐标系中,函数与的图象是(
)
10.
已知函数的定义域是[1,2],则函数的定义域是(
)
A.
[2,4]
B.
[4,16]
C.
[0,1]
D.
[1,2]
11.
已知函数,且g(x)的图象与f(x)的图象关于直线对称,则是(
)
A.
奇函数,且在(0,)上递减
B.
偶函数,且在(0,)上递增
C.
奇函数,且在(,0)上递减
D.
偶函数,且在(,0)上递增
二.
填空题
12.已知,当时,恒有,则m的取值范围是________________
(提示:①;②)
13.
求值
(1)_________
(2)_________
(3)_________
(4)已知,则_________
14.
函数是减函数,则a的取值范围是_________
15.
若,则a的取值范围是_________
16.
函数的单调递增区间是_________;单调递减区间是_________;值域是_________
三.
解答题
17.
已知在区间(,0)上是减函数,求f(x)的增区间。
解:设
在(,0)上
在上,
在上,____________________
在上,____________________
递增区间为:_______________
18.
已知常数a>1,变量x,y有关系:
(1)若,试以a,t表示y;
(2)若t在[1,)内变化时,y有最小值8,求此时a和x的值各为多少?
19.
对于函数,若存在,使成立,则称点(x0,x0)为函数的不动点
(1)已知函数有不动点(1,1)和(-3,-3),求a,b的值。
(2)若对于任意实数b,函数总有两个相异的不动点,求实数a的取值范围。
(3)若定义在实数集R上的奇函数存(有限的)n个不动点,求证n必为奇数。
【试题答案】
1.
B
2.
D
3.
C
4.
D
5.
C
6.
A
7.
B
8.
C
9.
B
10.
B
11.
D
12.
或
13.
(1);(2);(3)21;(4)
14.
15.
16.
,,
17.
,又;;
18.
解:(1)将代入原式,整理得
(2),
取最小值时,y取最小值
时,
由题意,得
19.
解:(1)由不动点定义有
把x=1代入得a=1,把a=1,x=-3代入得b=3
(2)与例9(2)相同,0
,是的一个不动点
若有异于(0,0)点的不动点(x0,x0),则
又,也是的不动点
的有限个不动点除原点处,都是成对出现的,有2k个,加上原点,共有n=2k+1个,∴n为奇数
