2.4.2 二次函数的性质 同步练习(含答案)
文档属性
| 名称 | 2.4.2 二次函数的性质 同步练习(含答案) | 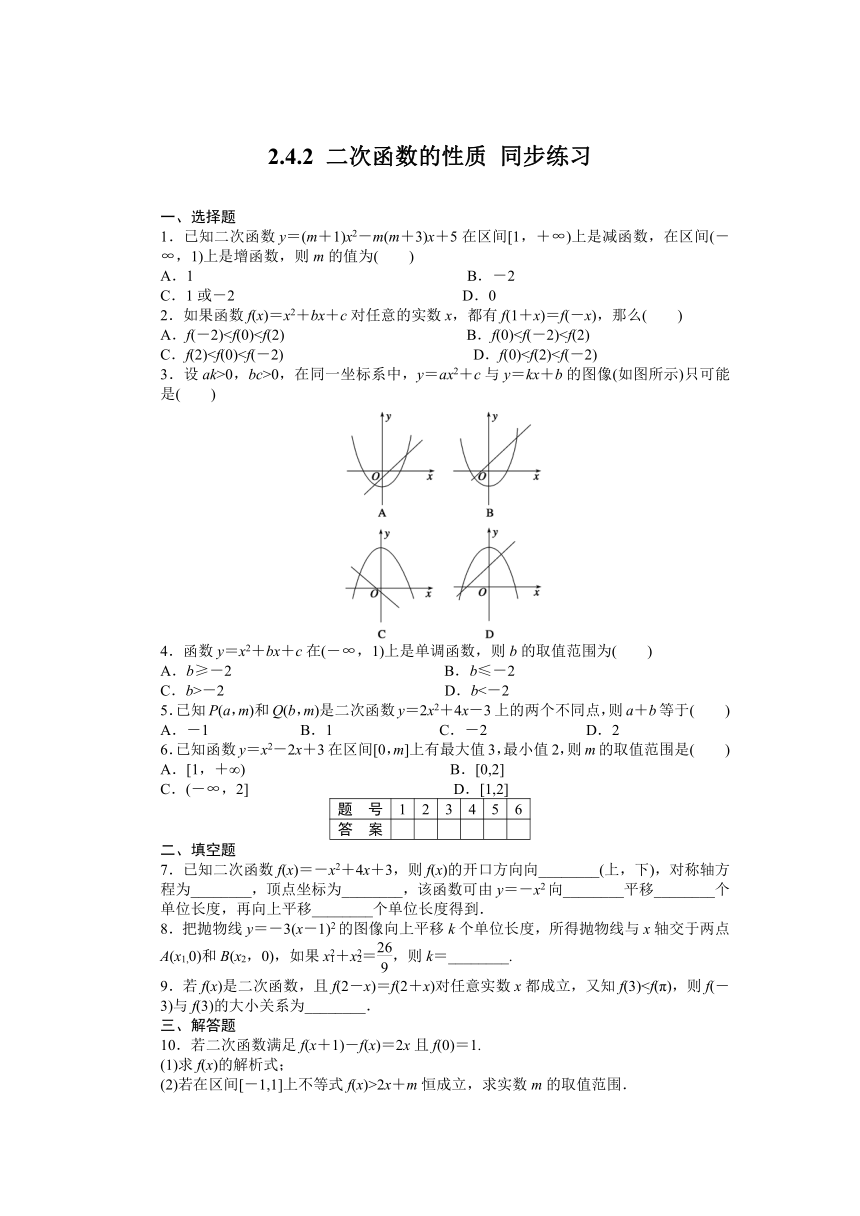 | |
| 格式 | zip | ||
| 文件大小 | 52.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-14 14:35:02 | ||
图片预览


文档简介
2.4.2
二次函数的性质
同步练习
一、选择题
1.已知二次函数y=(m+1)x2-m(m+3)x+5在区间[1,+∞)上是减函数,在区间(-∞,1)上是增函数,则m的值为( )
A.1
B.-2
C.1或-2
D.0
2.如果函数f(x)=x2+bx+c对任意的实数x,都有f(1+x)=f(-x),那么( )
A.f(-2)B.f(0)C.f(2)D.f(0)3.设ak>0,bc>0,在同一坐标系中,y=ax2+c与y=kx+b的图像(如图所示)只可能是( )
4.函数y=x2+bx+c在(-∞,1)上是单调函数,则b的取值范围为( )
A.b≥-2
B.b≤-2
C.b>-2
D.b<-2
5.已知P(a,m)和Q(b,m)是二次函数y=2x2+4x-3上的两个不同点,则a+b等于( )
A.-1
B.1
C.-2
D.2
6.已知函数y=x2-2x+3在区间[0,m]上有最大值3,最小值2,则m的取值范围是( )
A.[1,+∞)
B.[0,2]
C.(-∞,2]
D.[1,2]
题 号
1
2
3
4
5
6
答 案
二、填空题
7.已知二次函数f(x)=-x2+4x+3,则f(x)的开口方向向________(上,下),对称轴方程为________,顶点坐标为________,该函数可由y=-x2向________平移________个单位长度,再向上平移________个单位长度得到.
8.把抛物线y=-3(x-1)2的图像向上平移k个单位长度,所得抛物线与x轴交于两点A(x1,0)和B(x2,0),如果x+x=,则k=________.
9.若f(x)是二次函数,且f(2-x)=f(2+x)对任意实数x都成立,又知f(3)三、解答题
10.若二次函数满足f(x+1)-f(x)=2x且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[-1,1]上不等式f(x)>2x+m恒成立,求实数m的取值范围.
11.已知函数f(x)=x2-2x+2.
(1)求f(x)在区间[,3]上的最大值和最小值;
(2)若g(x)=f(x)-mx在[2,4]上是单调函数,求m的取值范围.
能力提升
12.已知函数f(x)=3-2|x|,g(x)=x2-2x,构造函数F(x),定义如下:当f(x)≥g(x)时,F(x)=g(x);当f(x)A.有最大值3,最小值-1
B.有最大值3,无最小值
C.有最大值7-2,无最小值
D.无最大值,也无最小值
13.已知函数f(x)=ax2-|x|+2a-1,其中a≥0,a∈R.
(1)若a=1,作函数f(x)的图像;
(2)设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式.
二次函数的性质
作业设计
1.B [由题设知对称轴为x=1,∴=1,
解得m=1或-2.
由已知知抛物线开口向下,∴m=-2.]
2.D [依题意,由f(1+x)=f(-x)知,二次函数的对称轴为x=,因为f(x)=x2+bx+c开口向上,且f(0)=f(1),f(-2)=f(3),由函数f(x)的图像可知,[,+∞)为f(x)的增区间,
所以f(1)3.A
4.B [由题意知:对称轴x=-≥1,b≤-2.]
5.C [由P、Q两点关于直线x=-1对称,
知P、Q的中点坐标为(-1,m),
∴=-1,即a+b=-2.]
6.D [由y=x2-2x+3=(x-1)2+2知,
当x=1时,y的最小值为2,
当y=3时,x2-2x+3=3,解得x=0或x=2.
由y=x2-2x+3的图像知,当m∈[1,2]时,能保证y的最大值为3,最小值为2.]
7.下 x=2 (2,7) 右 2 7
解析 ∵f(x)=-x2+4x+3=-(x-2)2+7,
由a=-1<0,可知f(x)的开口向下,对称轴方程为x=2,顶点坐标为(2,7),可由y=-x2向右平移2个单位长度,再向上平移7个单位长度得到.
8.
解析 y=-3(x-1)2+k,令y=0,
则3(x-1)2=k,即3x2-6x+3-k=0,
x1+x2=2,x1x2=,
∴x+x=(x1+x2)2-2x1x2=4-=,∴k=.
9.f(-3)>f(3)
解析 ∵f(2-x)=f(2+x)对任意实数x都成立,
∴f(x)的图像即函数的对称轴是直线x=2,
∴f(1)=f(3).
又∵f(3)∴抛物线的开口必然向上,即x∈(-∞,2)时,
f(x)单调递减,x∈[2,+∞)时,f(x)单调递增.
∴f(-3)>f(1).
∴f(-3)>f(3).
10.解 (1)设f(x)=ax2+bx+c(a≠0),由f(0)=1,∴c=1,
∴f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x,∴2ax+a+b=2x,
∴,∴,∴f(x)=x2-x+1.
(2)由题意:x2-x+1>2x+m在[-1,1]上恒成立,
即x2-3x+1-m>0在[-1,1]上恒成立.
令g(x)=x2-3x+1-m=(x-)2--m,
其对称轴为x=,
∴g(x)在区间[-1,1]上是减函数,
∴g(x)min=g(1)=1-3+1-m>0,∴m<-1.
11.解 (1)∵f(x)=x2-2x+2=(x-1)2+1,x∈[,3],
∴f(x)的最小值是f(1)=1,又f()=,f(3)=5,
所以,f(x)的最大值是f(3)=5,
即f(x)在区间[,3]上的最大值是5,最小值是1.
(2)∵g(x)=f(x)-mx=x2-(m+2)x+2,
∴≤2或≥4,
即m≤2或m≥6.
故m的取值范围是(-∞,2]∪[6,+∞).
12.C
[画图得到F(x)的图像:
射线AC、抛物线及射线BD三段,
联立方程组
得xA=2-,
代入得F(x)的最大值为7-2,
由图可得F(x)无最小值,从而选C.]
13.
解 (1)当a=1时,
f(x)=x2-|x|+1
=.
作图(如右所示)
(2)当x∈[1,2]时,f(x)=ax2-x+2a-1.
若a=0,则f(x)=-x-1在区间[1,2]上是减函数,
g(a)=f(2)=-3.
若a>0,则f(x)=a(x-)2+2a--1,
f(x)图像的对称轴是直线x=.
当0<<1,即a>时,f(x)在区间[1,2]上是增函数,
g(a)=f(1)=3a-2.
当1≤≤2,即≤a≤时,
g(a)=f()=2a--1,
当>2,即0g(a)=f(2)=6a-3.
综上可得g(a)=
二次函数的性质
同步练习
一、选择题
1.已知二次函数y=(m+1)x2-m(m+3)x+5在区间[1,+∞)上是减函数,在区间(-∞,1)上是增函数,则m的值为( )
A.1
B.-2
C.1或-2
D.0
2.如果函数f(x)=x2+bx+c对任意的实数x,都有f(1+x)=f(-x),那么( )
A.f(-2)
4.函数y=x2+bx+c在(-∞,1)上是单调函数,则b的取值范围为( )
A.b≥-2
B.b≤-2
C.b>-2
D.b<-2
5.已知P(a,m)和Q(b,m)是二次函数y=2x2+4x-3上的两个不同点,则a+b等于( )
A.-1
B.1
C.-2
D.2
6.已知函数y=x2-2x+3在区间[0,m]上有最大值3,最小值2,则m的取值范围是( )
A.[1,+∞)
B.[0,2]
C.(-∞,2]
D.[1,2]
题 号
1
2
3
4
5
6
答 案
二、填空题
7.已知二次函数f(x)=-x2+4x+3,则f(x)的开口方向向________(上,下),对称轴方程为________,顶点坐标为________,该函数可由y=-x2向________平移________个单位长度,再向上平移________个单位长度得到.
8.把抛物线y=-3(x-1)2的图像向上平移k个单位长度,所得抛物线与x轴交于两点A(x1,0)和B(x2,0),如果x+x=,则k=________.
9.若f(x)是二次函数,且f(2-x)=f(2+x)对任意实数x都成立,又知f(3)
10.若二次函数满足f(x+1)-f(x)=2x且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[-1,1]上不等式f(x)>2x+m恒成立,求实数m的取值范围.
11.已知函数f(x)=x2-2x+2.
(1)求f(x)在区间[,3]上的最大值和最小值;
(2)若g(x)=f(x)-mx在[2,4]上是单调函数,求m的取值范围.
能力提升
12.已知函数f(x)=3-2|x|,g(x)=x2-2x,构造函数F(x),定义如下:当f(x)≥g(x)时,F(x)=g(x);当f(x)
B.有最大值3,无最小值
C.有最大值7-2,无最小值
D.无最大值,也无最小值
13.已知函数f(x)=ax2-|x|+2a-1,其中a≥0,a∈R.
(1)若a=1,作函数f(x)的图像;
(2)设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式.
二次函数的性质
作业设计
1.B [由题设知对称轴为x=1,∴=1,
解得m=1或-2.
由已知知抛物线开口向下,∴m=-2.]
2.D [依题意,由f(1+x)=f(-x)知,二次函数的对称轴为x=,因为f(x)=x2+bx+c开口向上,且f(0)=f(1),f(-2)=f(3),由函数f(x)的图像可知,[,+∞)为f(x)的增区间,
所以f(1)
4.B [由题意知:对称轴x=-≥1,b≤-2.]
5.C [由P、Q两点关于直线x=-1对称,
知P、Q的中点坐标为(-1,m),
∴=-1,即a+b=-2.]
6.D [由y=x2-2x+3=(x-1)2+2知,
当x=1时,y的最小值为2,
当y=3时,x2-2x+3=3,解得x=0或x=2.
由y=x2-2x+3的图像知,当m∈[1,2]时,能保证y的最大值为3,最小值为2.]
7.下 x=2 (2,7) 右 2 7
解析 ∵f(x)=-x2+4x+3=-(x-2)2+7,
由a=-1<0,可知f(x)的开口向下,对称轴方程为x=2,顶点坐标为(2,7),可由y=-x2向右平移2个单位长度,再向上平移7个单位长度得到.
8.
解析 y=-3(x-1)2+k,令y=0,
则3(x-1)2=k,即3x2-6x+3-k=0,
x1+x2=2,x1x2=,
∴x+x=(x1+x2)2-2x1x2=4-=,∴k=.
9.f(-3)>f(3)
解析 ∵f(2-x)=f(2+x)对任意实数x都成立,
∴f(x)的图像即函数的对称轴是直线x=2,
∴f(1)=f(3).
又∵f(3)
f(x)单调递减,x∈[2,+∞)时,f(x)单调递增.
∴f(-3)>f(1).
∴f(-3)>f(3).
10.解 (1)设f(x)=ax2+bx+c(a≠0),由f(0)=1,∴c=1,
∴f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x,∴2ax+a+b=2x,
∴,∴,∴f(x)=x2-x+1.
(2)由题意:x2-x+1>2x+m在[-1,1]上恒成立,
即x2-3x+1-m>0在[-1,1]上恒成立.
令g(x)=x2-3x+1-m=(x-)2--m,
其对称轴为x=,
∴g(x)在区间[-1,1]上是减函数,
∴g(x)min=g(1)=1-3+1-m>0,∴m<-1.
11.解 (1)∵f(x)=x2-2x+2=(x-1)2+1,x∈[,3],
∴f(x)的最小值是f(1)=1,又f()=,f(3)=5,
所以,f(x)的最大值是f(3)=5,
即f(x)在区间[,3]上的最大值是5,最小值是1.
(2)∵g(x)=f(x)-mx=x2-(m+2)x+2,
∴≤2或≥4,
即m≤2或m≥6.
故m的取值范围是(-∞,2]∪[6,+∞).
12.C
[画图得到F(x)的图像:
射线AC、抛物线及射线BD三段,
联立方程组
得xA=2-,
代入得F(x)的最大值为7-2,
由图可得F(x)无最小值,从而选C.]
13.
解 (1)当a=1时,
f(x)=x2-|x|+1
=.
作图(如右所示)
(2)当x∈[1,2]时,f(x)=ax2-x+2a-1.
若a=0,则f(x)=-x-1在区间[1,2]上是减函数,
g(a)=f(2)=-3.
若a>0,则f(x)=a(x-)2+2a--1,
f(x)图像的对称轴是直线x=.
当0<<1,即a>时,f(x)在区间[1,2]上是增函数,
g(a)=f(1)=3a-2.
当1≤≤2,即≤a≤时,
g(a)=f()=2a--1,
当>2,即0
综上可得g(a)=
