3.3 指数函数 学案2(含答案)
图片预览




文档简介
3.3
指数函数
学案
1.理解指数函数的概念.
2.掌握指数函数的图像和性质.
3.利用指数函数的图像和性质解决简单问题.
1.指数函数的定义
函数y=ax(a>0,a≠1)叫作指数函数,其中____是自变量.
指数函数y=ax(a>0,a≠1)解析式的结构特征:
①底数:大于零且不等于1的常数;
②指数:自变量x;
③系数:1.
指数函数解析式的结构的三个特征是判断函数是否为指数函数的三个标准,缺一不可.
【做一做1】
下列函数是指数函数的是(
).
A.y=(-3)x
B.y=-3x
C.y=32x
D.y=2x+1
2.指数函数的图像和性质
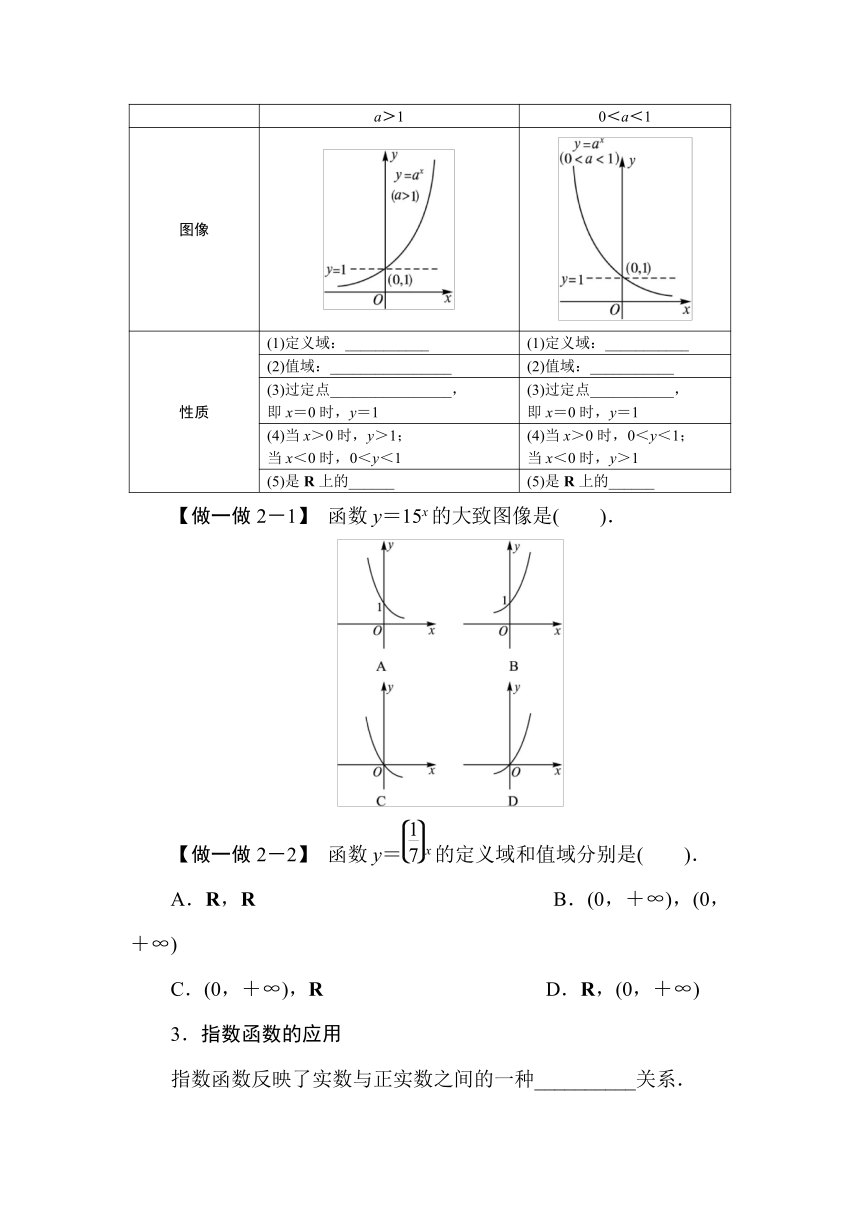
结合函数y=2x和y=x的图像和性质,得出指数函数的图像和性质,如下表所示:
a>1
0<a<1
图像
性质
(1)定义域:___________
(1)定义域:___________
(2)值域:________________
(2)值域:___________
(3)过定点________________,即x=0时,y=1
(3)过定点___________,即x=0时,y=1
(4)当x>0时,y>1;当x<0时,0<y<1
(4)当x>0时,0<y<1;当x<0时,y>1
(5)是R上的______
(5)是R上的______
【做一做2-1】
函数y=15x的大致图像是(
).
【做一做2-2】
函数y=x的定义域和值域分别是(
).
A.R,R
B.(0,+∞),(0,+∞)
C.(0,+∞),R
D.R,(0,+∞)
3.指数函数的应用
指数函数反映了实数与正实数之间的一种__________关系.
指数幂ax和1的比较:
当x<0,0<a<1或x>0,a>1时,ax>1,即指数x和0比较,底数a和1比较,当不等号的方向相同时,ax大于1,简称为“同大”.
当x<0,a>1或x>0,0<a<1时,
0<ax<1,即指数x和0比较,底数a和1比较,当不等号的方向相反(异)时,ax小于1,简称为“异小”.
因此简称为“同大异小”.
【做一做3】
比较下列各题中两个值的大小:
(1)1.82.2__________1.83;
(2)0.7-0.3__________0.7-0.4;
(3)1.90.4__________0.92.4.
答案:1.x
【做一做1】
C ∵32x=9x,∴y=32x=9x是指数函数.
2.(1)R (1)R (2)(0,+∞) (2)(0,+∞) (3)(0,1)
(3)(0,1) (5)增函数 (5)减函数
【做一做2-1】
B
【做一做2-2】
D
3.一一对应
【做一做3】
(1)< (2)< (3)>
指数函数y=ax(a>0,a≠1)中底数a对函数图像有什么影响?
剖析:设a>b>1>c>d>0,则y=ax,y=bx,y=cx,y=dx的图像如图所示,从图中可以看出:在y轴右侧,图像从上到下相应的底数由大变小,在y轴左侧,图像从下到上相应的底数由大变小,即无论在y轴的左侧还是右侧,底数按逆时针方向变大.
或者说在第一象限内,指数函数的图像,底数大的在上边,也可以说底数越大越靠近y轴.
题型一
指数函数的定义
【例1】
指出下列函数中哪些是指数函数.
①y=6x;②y=x4;③y=-4x;④y=(-4)x;⑤y=2·8x;⑥y=ex;⑦y=4x2;⑧y=(2a-1)x.
分析:根据指数函数的定义进行判断.
题型二
求函数的定义域和值域
【例2】
求下列函数的定义域和值域:
(1)y=;
(2)y=;
(3)y=.
分析:函数的定义域是使函数有意义的自变量的取值范围,分式问题要使分母不为0,根式问题要使被开方数有意义,结合换元法,联想函数的图像,根据单调性等确定值域.
反思:求与指数函数有关的函数定义域和值域时,要充分考虑指数函数本身的要求,并利用好指数函数的单调性.对于解析式中某些较复杂的式子,往往采用换元法求解,这样可以使问题变得简洁,避免出错.
题型三
比较大小
【例3】
比较下列各题中两个值的大小:
(1)1.72.5,1.73;
(2)2.3-0.28,0.67-3.1.
分析:(1)构造指数函数,利用其单调性比较大小;(2)利用中间量1比较大小.
反思:比较指数式大小的方法:
(1)单调性法:比较同底数幂的大小,可构造指数函数,利用指数函数的单调性比较大小.要注意:明确所给的两个值是哪个指数函数的两个函数值;明确指数函数的底数与1的大小关系;最后根据指数函数的图像和性质来判断.
(2)中间量法:比较不同底且不同指数幂的大小,常借助于中间值1进行比较.利用口诀“同大异小”,判断指数幂和1的大小.
题型四
指数函数的单调性的应用
【例4】
设a为实数,f(x)=a-(x∈R).
(1)证明f(x)在R上为增函数;
(2)试确定a的值,使f(x)为奇函数.
分析:对于(1)可结合单调性的定义及y=2x为增函数加以证明.(2)中要使f(x)是奇函数,则须满足f(-x)=-f(x).
反思:本题主要考查了单调性和奇偶性的概念及使用方法.在本题(2)中,由于f(x)为奇函数且在x=0处有定义,故也可利用f(0)=0来确定a的值.
题型五
与指数函数图像有关的问题
【例5】
(1)将函数y=3x的图像向左平移一个单位即可得到函数________的图像,将y=3x的图像向下平移一个单位即可得到函数________的图像;
(2)函数y=3x的图像与y=3-x的图像关于________对称;
(3)函数y=3x的图像与y=-3x的图像关于________对称;
(4)函数y=3x的图像与函数y=-3-x的图像关于________对称.
反思:1.平移规律
分左、右平移和上、下平移两种,遵循“左加右减,上加下减”.
若已知y=ax的图像,把y=ax的图像向左平移b(b>0)个单位,则得到y=ax+b的图像;把y=ax的图像向右平移b(b>0)个单位,则得到y=ax-b的图像;把y=ax的图像向上平移b(b>0)个单位,则得到y=ax+b的图像,向下平移b(b>0)个单位,则得到y=ax-b的图像.
2.对称规律
函数y=ax的图像与y=a-x的图像关于y轴对称;y=ax的图像与y=-ax的图像关于x轴对称,函数y=ax的图像与y=-a-x的图像关于坐标原点对称.
题型六
易错辨析
易错点
利用换元法时,忽略新元的范围导致出错.
【例6】
求函数y=x+x+1的值域.
错解:令t=x,则原函数可化为y=t2+t+1=2+≥,即当t=-时,ymin=,即原函数的值域是.
错因分析:错解在令t=x后,没有注意新元t的范围.∵x>0,∴t>0.忽略新元的范围导致所求范围扩大.
答案:【例1】
解:①⑥⑧为指数函数;②不是指数函数,自变量不在指数上;③4x的系数是-1;④中底数-4<0,所以不是指数函数;⑤8x的系数是2;⑦中指数不是自变量x,而是x的函数x2,故②③④⑤⑦都不是指数函数.
【例2】
解:(1)要使函数有意义,必须x-4≠0,
∴x≠4,
故所求函数的定义域为{x∈R|x≠4}.
∵x≠4,≠0,∴≠1,
故函数的值域为{y|y>0且y≠1}.
(2)定义域为R.
∵2x-x2=-(x-1)2+1≤1,
∴≥1=,
故函数y=的值域为{y|y≥}.
(3)要使函数有意义,必须且只需3x-2≥0,即x≥,
∴函数的定义域为.
设t=,则t≥0,y=5t,
∴y≥50=1,故所求函数的值域为[1,+∞).
【例3】
解:(1)(单调性法)由于1.72.5与1.73的底数是1.7,
故构造函数y=1.7x,
则函数y=1.7x在R上是增函数.
又2.5<3,所以1.72.5<1.73.
(2)(中间量法)由指数函数的性质,知
2.3-0.28<2.30=1,0.67-3.1>0.670=1,
所以2.3-0.28<0.67-3.1.
【例4】
解:(1)证明:设x1,x2∈R,x1<x2,则
f(x1)-f(x2)
=-
=.
由于指数函数y=2x在R上为增函数,且x1<x2,
所以2x1<2
x2,即2
x1-2
x2<0.
又由2x>0,得2
x1+1>0,2
x2+1>0.
所以f(x1)-f(x2)<0,即f(x1)<f(x2).
故f(x)在R上为增函数.
(2)若f(x)为奇函数,则f(-x)=-f(x),
即a-=-.
变形得2a=+
=+==2.
解得a=1.所以当a=1时,f(x)为奇函数.
【例5】
(1)y=3x+1 y=3x-1 (2)y轴 (3)x轴 (4)原点
(1)根据函数图像平移的规律来解决.
(2)∵函数y=3x中用-x代x,y不变,即得y=3-x,
∴关于y轴对称;
(3)∵函数y=3x中用-y代y,x不变,即得y=-3x,
∴关于x轴对称.
(4)∵函数y=3x中用-x代x,用-y代y,即得y=-3-x,∴关于原点对称.
【例6】
正解:令t=x,则t∈(0,+∞),原函数可化为y=t2+t+1=2+.
因为函数y=2+在(0,+∞)上是增加的,所以y>1,即原函数的值域是(1,+∞).
1
函数f(x)=ax在R上是增函数,则实数a的取值范围是(
).
A.0<a<1
B.a<1
C.a>1
D.R
2
函数y=0.22x的大致图像是(
).
3
函数y=的值域是(
).
A.(-∞,0)
B.(0,1]
C.[1,+∞)
D.(-∞,1]
4
函数f(x)=a3-x+1(a>0,a≠1)的图像恒过定点的坐标是__________.
5
比较下列各题中两个值的大小:
(1)0.8-0.1,0.8-0.2;
(2)1.70.3,0.93.1;
(3)a1.3,a2.5(a>0,a≠1).
答案:1.C 2.B 3.B
4.(3,2) 当x=3时,对于a>0且a≠1总有f(3)=a0+1=2,即过定点(3,2).
5.分析:(1)由于底数相同,利用单调性法比较大小;(2)由于底数和指数均不同,用中间量法比较大小;(3)对底数a按与1的大小关系分类讨论.
解:(1)由于0<0.8<1,所以指数函数y=0.8x在R上为减函数.
所以0.8-0.1<0.8-0.2.
(2)1.70.3>1,0.93.1<1,所以1.70.3>0.93.1.
(3)当a>1时,函数y=ax在R上是增函数,此时a1.3<a2.5;
当0<a<1时,函数y=ax在R上是减函数,此时a1.3>a2.5.
即当a>1时,a1.3<a2.5;
当0<a<1时,a1.3>a2.5.
指数函数
学案
1.理解指数函数的概念.
2.掌握指数函数的图像和性质.
3.利用指数函数的图像和性质解决简单问题.
1.指数函数的定义
函数y=ax(a>0,a≠1)叫作指数函数,其中____是自变量.
指数函数y=ax(a>0,a≠1)解析式的结构特征:
①底数:大于零且不等于1的常数;
②指数:自变量x;
③系数:1.
指数函数解析式的结构的三个特征是判断函数是否为指数函数的三个标准,缺一不可.
【做一做1】
下列函数是指数函数的是(
).
A.y=(-3)x
B.y=-3x
C.y=32x
D.y=2x+1
2.指数函数的图像和性质
结合函数y=2x和y=x的图像和性质,得出指数函数的图像和性质,如下表所示:
a>1
0<a<1
图像
性质
(1)定义域:___________
(1)定义域:___________
(2)值域:________________
(2)值域:___________
(3)过定点________________,即x=0时,y=1
(3)过定点___________,即x=0时,y=1
(4)当x>0时,y>1;当x<0时,0<y<1
(4)当x>0时,0<y<1;当x<0时,y>1
(5)是R上的______
(5)是R上的______
【做一做2-1】
函数y=15x的大致图像是(
).
【做一做2-2】
函数y=x的定义域和值域分别是(
).
A.R,R
B.(0,+∞),(0,+∞)
C.(0,+∞),R
D.R,(0,+∞)
3.指数函数的应用
指数函数反映了实数与正实数之间的一种__________关系.
指数幂ax和1的比较:
当x<0,0<a<1或x>0,a>1时,ax>1,即指数x和0比较,底数a和1比较,当不等号的方向相同时,ax大于1,简称为“同大”.
当x<0,a>1或x>0,0<a<1时,
0<ax<1,即指数x和0比较,底数a和1比较,当不等号的方向相反(异)时,ax小于1,简称为“异小”.
因此简称为“同大异小”.
【做一做3】
比较下列各题中两个值的大小:
(1)1.82.2__________1.83;
(2)0.7-0.3__________0.7-0.4;
(3)1.90.4__________0.92.4.
答案:1.x
【做一做1】
C ∵32x=9x,∴y=32x=9x是指数函数.
2.(1)R (1)R (2)(0,+∞) (2)(0,+∞) (3)(0,1)
(3)(0,1) (5)增函数 (5)减函数
【做一做2-1】
B
【做一做2-2】
D
3.一一对应
【做一做3】
(1)< (2)< (3)>
指数函数y=ax(a>0,a≠1)中底数a对函数图像有什么影响?
剖析:设a>b>1>c>d>0,则y=ax,y=bx,y=cx,y=dx的图像如图所示,从图中可以看出:在y轴右侧,图像从上到下相应的底数由大变小,在y轴左侧,图像从下到上相应的底数由大变小,即无论在y轴的左侧还是右侧,底数按逆时针方向变大.
或者说在第一象限内,指数函数的图像,底数大的在上边,也可以说底数越大越靠近y轴.
题型一
指数函数的定义
【例1】
指出下列函数中哪些是指数函数.
①y=6x;②y=x4;③y=-4x;④y=(-4)x;⑤y=2·8x;⑥y=ex;⑦y=4x2;⑧y=(2a-1)x.
分析:根据指数函数的定义进行判断.
题型二
求函数的定义域和值域
【例2】
求下列函数的定义域和值域:
(1)y=;
(2)y=;
(3)y=.
分析:函数的定义域是使函数有意义的自变量的取值范围,分式问题要使分母不为0,根式问题要使被开方数有意义,结合换元法,联想函数的图像,根据单调性等确定值域.
反思:求与指数函数有关的函数定义域和值域时,要充分考虑指数函数本身的要求,并利用好指数函数的单调性.对于解析式中某些较复杂的式子,往往采用换元法求解,这样可以使问题变得简洁,避免出错.
题型三
比较大小
【例3】
比较下列各题中两个值的大小:
(1)1.72.5,1.73;
(2)2.3-0.28,0.67-3.1.
分析:(1)构造指数函数,利用其单调性比较大小;(2)利用中间量1比较大小.
反思:比较指数式大小的方法:
(1)单调性法:比较同底数幂的大小,可构造指数函数,利用指数函数的单调性比较大小.要注意:明确所给的两个值是哪个指数函数的两个函数值;明确指数函数的底数与1的大小关系;最后根据指数函数的图像和性质来判断.
(2)中间量法:比较不同底且不同指数幂的大小,常借助于中间值1进行比较.利用口诀“同大异小”,判断指数幂和1的大小.
题型四
指数函数的单调性的应用
【例4】
设a为实数,f(x)=a-(x∈R).
(1)证明f(x)在R上为增函数;
(2)试确定a的值,使f(x)为奇函数.
分析:对于(1)可结合单调性的定义及y=2x为增函数加以证明.(2)中要使f(x)是奇函数,则须满足f(-x)=-f(x).
反思:本题主要考查了单调性和奇偶性的概念及使用方法.在本题(2)中,由于f(x)为奇函数且在x=0处有定义,故也可利用f(0)=0来确定a的值.
题型五
与指数函数图像有关的问题
【例5】
(1)将函数y=3x的图像向左平移一个单位即可得到函数________的图像,将y=3x的图像向下平移一个单位即可得到函数________的图像;
(2)函数y=3x的图像与y=3-x的图像关于________对称;
(3)函数y=3x的图像与y=-3x的图像关于________对称;
(4)函数y=3x的图像与函数y=-3-x的图像关于________对称.
反思:1.平移规律
分左、右平移和上、下平移两种,遵循“左加右减,上加下减”.
若已知y=ax的图像,把y=ax的图像向左平移b(b>0)个单位,则得到y=ax+b的图像;把y=ax的图像向右平移b(b>0)个单位,则得到y=ax-b的图像;把y=ax的图像向上平移b(b>0)个单位,则得到y=ax+b的图像,向下平移b(b>0)个单位,则得到y=ax-b的图像.
2.对称规律
函数y=ax的图像与y=a-x的图像关于y轴对称;y=ax的图像与y=-ax的图像关于x轴对称,函数y=ax的图像与y=-a-x的图像关于坐标原点对称.
题型六
易错辨析
易错点
利用换元法时,忽略新元的范围导致出错.
【例6】
求函数y=x+x+1的值域.
错解:令t=x,则原函数可化为y=t2+t+1=2+≥,即当t=-时,ymin=,即原函数的值域是.
错因分析:错解在令t=x后,没有注意新元t的范围.∵x>0,∴t>0.忽略新元的范围导致所求范围扩大.
答案:【例1】
解:①⑥⑧为指数函数;②不是指数函数,自变量不在指数上;③4x的系数是-1;④中底数-4<0,所以不是指数函数;⑤8x的系数是2;⑦中指数不是自变量x,而是x的函数x2,故②③④⑤⑦都不是指数函数.
【例2】
解:(1)要使函数有意义,必须x-4≠0,
∴x≠4,
故所求函数的定义域为{x∈R|x≠4}.
∵x≠4,≠0,∴≠1,
故函数的值域为{y|y>0且y≠1}.
(2)定义域为R.
∵2x-x2=-(x-1)2+1≤1,
∴≥1=,
故函数y=的值域为{y|y≥}.
(3)要使函数有意义,必须且只需3x-2≥0,即x≥,
∴函数的定义域为.
设t=,则t≥0,y=5t,
∴y≥50=1,故所求函数的值域为[1,+∞).
【例3】
解:(1)(单调性法)由于1.72.5与1.73的底数是1.7,
故构造函数y=1.7x,
则函数y=1.7x在R上是增函数.
又2.5<3,所以1.72.5<1.73.
(2)(中间量法)由指数函数的性质,知
2.3-0.28<2.30=1,0.67-3.1>0.670=1,
所以2.3-0.28<0.67-3.1.
【例4】
解:(1)证明:设x1,x2∈R,x1<x2,则
f(x1)-f(x2)
=-
=.
由于指数函数y=2x在R上为增函数,且x1<x2,
所以2x1<2
x2,即2
x1-2
x2<0.
又由2x>0,得2
x1+1>0,2
x2+1>0.
所以f(x1)-f(x2)<0,即f(x1)<f(x2).
故f(x)在R上为增函数.
(2)若f(x)为奇函数,则f(-x)=-f(x),
即a-=-.
变形得2a=+
=+==2.
解得a=1.所以当a=1时,f(x)为奇函数.
【例5】
(1)y=3x+1 y=3x-1 (2)y轴 (3)x轴 (4)原点
(1)根据函数图像平移的规律来解决.
(2)∵函数y=3x中用-x代x,y不变,即得y=3-x,
∴关于y轴对称;
(3)∵函数y=3x中用-y代y,x不变,即得y=-3x,
∴关于x轴对称.
(4)∵函数y=3x中用-x代x,用-y代y,即得y=-3-x,∴关于原点对称.
【例6】
正解:令t=x,则t∈(0,+∞),原函数可化为y=t2+t+1=2+.
因为函数y=2+在(0,+∞)上是增加的,所以y>1,即原函数的值域是(1,+∞).
1
函数f(x)=ax在R上是增函数,则实数a的取值范围是(
).
A.0<a<1
B.a<1
C.a>1
D.R
2
函数y=0.22x的大致图像是(
).
3
函数y=的值域是(
).
A.(-∞,0)
B.(0,1]
C.[1,+∞)
D.(-∞,1]
4
函数f(x)=a3-x+1(a>0,a≠1)的图像恒过定点的坐标是__________.
5
比较下列各题中两个值的大小:
(1)0.8-0.1,0.8-0.2;
(2)1.70.3,0.93.1;
(3)a1.3,a2.5(a>0,a≠1).
答案:1.C 2.B 3.B
4.(3,2) 当x=3时,对于a>0且a≠1总有f(3)=a0+1=2,即过定点(3,2).
5.分析:(1)由于底数相同,利用单调性法比较大小;(2)由于底数和指数均不同,用中间量法比较大小;(3)对底数a按与1的大小关系分类讨论.
解:(1)由于0<0.8<1,所以指数函数y=0.8x在R上为减函数.
所以0.8-0.1<0.8-0.2.
(2)1.70.3>1,0.93.1<1,所以1.70.3>0.93.1.
(3)当a>1时,函数y=ax在R上是增函数,此时a1.3<a2.5;
当0<a<1时,函数y=ax在R上是减函数,此时a1.3>a2.5.
即当a>1时,a1.3<a2.5;
当0<a<1时,a1.3>a2.5.
