3.3 指数函数(二)学案6(含答案)
文档属性
| 名称 | 3.3 指数函数(二)学案6(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 201.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-08-15 22:05:38 | ||
图片预览

文档简介
3.3 指数函数(二)
学案
课时目标 1.理解指数函数的单调性与底数a的关系,能运用指数函数的单调性解决一些问题.2.理解指数函数的底数a对函数图象的影响.
1.下列一定是指数函数的是________.
①y=-3x;②y=xx(x>0,且x≠1);③y=(a-2)x(a>3);④y=(1-)x.
2.指数函数y=ax与y=bx的图象如图,则0,a,b,1的大小关系为________.
3.函数y=πx的值域是________.
4.已知集合M={-1,1},N={x|<2x+1<4,x∈Z},则M∩N=________.
5.若()2a+1<()3-2a,则实数a的取值范围是______________.
6.若指数函数f(x)=(a+1)x是R上的减函数,那么a的取值范围为________.
一、填空题
1.设P={y|y=x2,x∈R},Q={y|y=2x,x∈R},则P、Q的关系为________.
2.函数y=的值域是________.
3.函数y=ax在[0,1]上的最大值与最小值的和为3,则函数y=2ax-1在[0,1]上的最大值是________.
4.若函数f(x)=3x+3-x与g(x)=3x-3-x的定义域均为R,则下列命题正确的是________.(填序号)
①f(x)与g(x)均为偶函数;
②f(x)为偶函数,g(x)为奇函数;
③f(x)与g(x)均为奇函数;
④f(x)为奇函数,g(x)为偶函数.
5.函数y=f(x)的图象与函数g(x)=ex+2的图象关于原点对称,则f(x)的解析式为________.
6.已知a=,b=,c=,则a,b,c三个数的大小关系是________.
7.春天来了,某池塘中的荷花枝繁叶茂,已知每一天新长出荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,当荷叶刚好覆盖水面面积一半时,荷叶已生长了________天.
8.已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=1-2-x,则不等式f(x)<-的解集是________.
9.函数y=的单调递增区间是________.
二、解答题
10.(1)设f(x)=2u,u=g(x),g(x)是R上的单调增函数,试判断f(x)的单调性;
(2)求函数y=的单调区间.
11.函数f(x)=4x-2x+1+3的定义域为[-,].
(1)设t=2x,求t的取值范围;
(2)求函数f(x)的值域.
能力提升
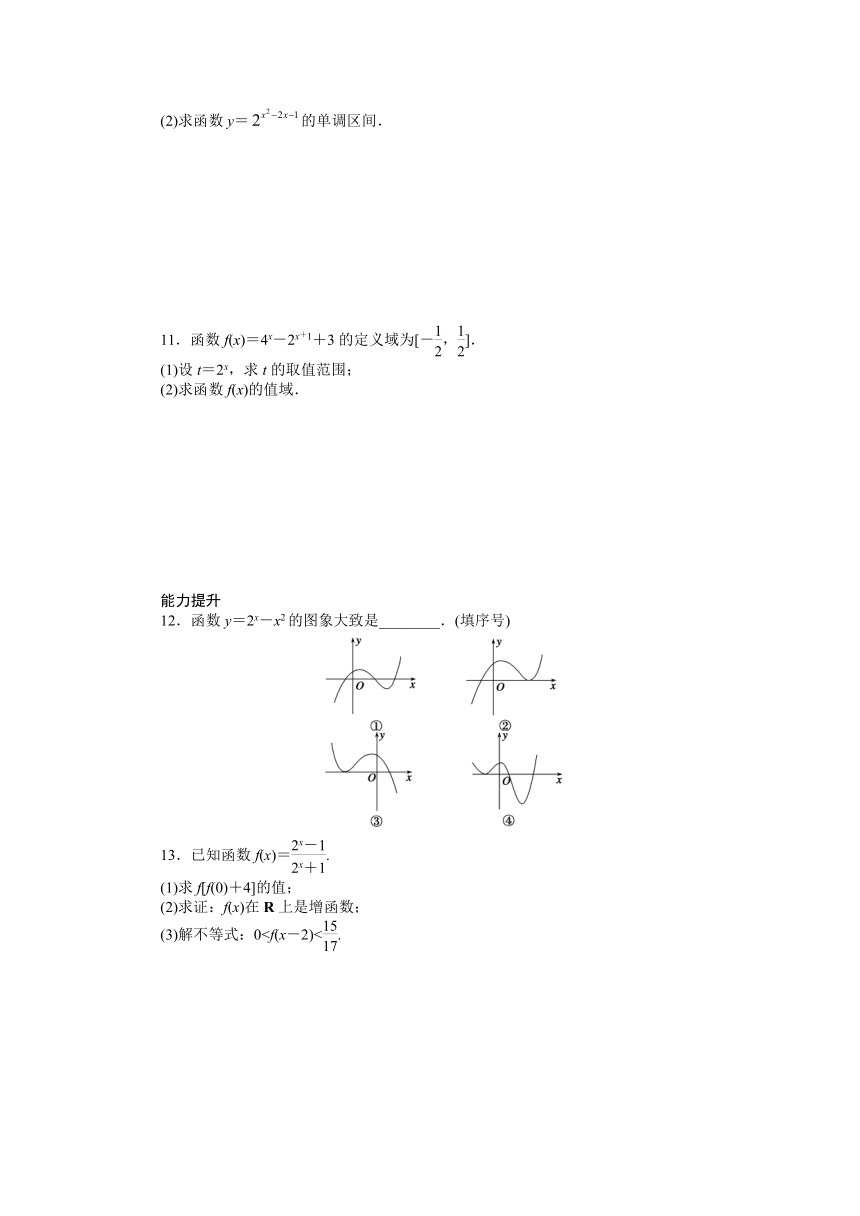
12.函数y=2x-x2的图象大致是________.(填序号)
13.已知函数f(x)=.
(1)求f[f(0)+4]的值;
(2)求证:f(x)在R上是增函数;
(3)解不等式:01.比较两个指数式值的大小主要有以下方法:
(1)比较形如am与an的大小,可运用指数函数y=ax的单调性.
(2)比较形如am与bn的大小,一般找一个“中间值c”,若amc且c>bn,则am>bn.
2.了解由y=f(u)及u=φ(x)的单调性探求y=f[φ(x)]的单调性的一般方法.
3.3 指数函数(二)
答案
双基演练
1.③
2.03.(0,+∞)
4.{-1}
解析 解指数不等式<2x+1<4,得-1所以-2所以M∩N={-1,1}∩{-1,0}={-1}.
5.(,+∞)
解析 ∵函数y=()x在R上为减函数,
∴2a+1>3-2a,∴a>.
6.-1作业设计
1.QP
解析 因为P={y|y≥0},Q={y|y>0},所以QP.
2.[0,4)
解析 ∵4x>0,∴0≤16-4x<16,
∴∈[0,4).
3.3
解析 函数y=ax在[0,1]上是单调的,最大值与最小值都在端点处取到,故有a0+a1=3,解得a=2,因此函数y=2ax-1=4x-1在[0,1]上是单调递增函数,当x=1时,ymax=3.
4.②
解析 f(-x)=3-x+3x=f(x),
g(-x)=3-x-3x=-g(x).
5.f(x)=-e-x-2
解析 ∵y=f(x)的图象与g(x)=ex+2的图象关于原点对称,
∴f(x)=-g(-x)=-(e-x+2)=-e-x-2.
6.c解析 ∵y=()x是减函数,->-,
∴b>a>1.又07.19
解析 假设第一天荷叶覆盖水面面积为1,则荷叶覆盖水面面积y与生长时间的函数关系为y=2x-1,当x=20时,长满水面,所以生长19天时,荷叶布满水面一半.
8.(-∞,-1)
解析 ∵f(x)是定义在R上的奇函数,
∴f(0)=0.
当x<0时,f(x)=-f(-x)=-(1-2x)=2x-1.
当x>0时,由1-2-x<-,()x>,得x∈ ;
当x=0时,f(0)=0<-不成立;
当x<0时,由2x-1<-,2x<2-1,得x<-1.
综上可知x∈(-∞,-1).
9.[1,+∞)
解析 利用复合函数同增异减的判断方法去判断.
令u=-x2+2x,则y=()u在u∈R上为减函数,问题转化为求u=-x2+2x的单调递减区间,即为x∈[1,+∞).
10.解 (1)设x1又由y=2u的增减性得<,即f(x1)所以f(x)为R上的增函数.
(2)令u=x2-2x-1=(x-1)2-2,
则u在区间[1,+∞)上为增函数.
根据(1)可知y=在[1,+∞)上为增函数.
同理可得函数y在(-∞,1]上为单调减函数.
即函数y的增区间为[1,+∞),减区间为(-∞,1].
11.解 (1)∵t=2x在x∈[-,]上单调递增,
∴t∈[,].
(2)函数可化为:f(x)=g(t)=t2-2t+3,
g(t)在[,1]上递减,在[1,]上递增,
比较得g()∴f(x)min=g(1)=2,
f(x)max=g()=5-2.
∴函数的值域为[2,5-2].
12.①
解析 当x→-∞时,2x→0,所以y=2x-x2→-∞,
所以排除③、④.
当x=3时,y=-1,所以排除②.
13.(1)解 ∵f(0)==0,
∴f[f(0)+4]=f(0+4)=f(4)==.
(2)证明 设x1,x2∈R且x1则>>0,->0,
∴f(x2)-f(x1)=
=>0,
即f(x1)(3)解 由0又f(x)在R上是增函数,∴0即2
学案
课时目标 1.理解指数函数的单调性与底数a的关系,能运用指数函数的单调性解决一些问题.2.理解指数函数的底数a对函数图象的影响.
1.下列一定是指数函数的是________.
①y=-3x;②y=xx(x>0,且x≠1);③y=(a-2)x(a>3);④y=(1-)x.
2.指数函数y=ax与y=bx的图象如图,则0,a,b,1的大小关系为________.
3.函数y=πx的值域是________.
4.已知集合M={-1,1},N={x|<2x+1<4,x∈Z},则M∩N=________.
5.若()2a+1<()3-2a,则实数a的取值范围是______________.
6.若指数函数f(x)=(a+1)x是R上的减函数,那么a的取值范围为________.
一、填空题
1.设P={y|y=x2,x∈R},Q={y|y=2x,x∈R},则P、Q的关系为________.
2.函数y=的值域是________.
3.函数y=ax在[0,1]上的最大值与最小值的和为3,则函数y=2ax-1在[0,1]上的最大值是________.
4.若函数f(x)=3x+3-x与g(x)=3x-3-x的定义域均为R,则下列命题正确的是________.(填序号)
①f(x)与g(x)均为偶函数;
②f(x)为偶函数,g(x)为奇函数;
③f(x)与g(x)均为奇函数;
④f(x)为奇函数,g(x)为偶函数.
5.函数y=f(x)的图象与函数g(x)=ex+2的图象关于原点对称,则f(x)的解析式为________.
6.已知a=,b=,c=,则a,b,c三个数的大小关系是________.
7.春天来了,某池塘中的荷花枝繁叶茂,已知每一天新长出荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,当荷叶刚好覆盖水面面积一半时,荷叶已生长了________天.
8.已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=1-2-x,则不等式f(x)<-的解集是________.
9.函数y=的单调递增区间是________.
二、解答题
10.(1)设f(x)=2u,u=g(x),g(x)是R上的单调增函数,试判断f(x)的单调性;
(2)求函数y=的单调区间.
11.函数f(x)=4x-2x+1+3的定义域为[-,].
(1)设t=2x,求t的取值范围;
(2)求函数f(x)的值域.
能力提升
12.函数y=2x-x2的图象大致是________.(填序号)
13.已知函数f(x)=.
(1)求f[f(0)+4]的值;
(2)求证:f(x)在R上是增函数;
(3)解不等式:0
(1)比较形如am与an的大小,可运用指数函数y=ax的单调性.
(2)比较形如am与bn的大小,一般找一个“中间值c”,若am
2.了解由y=f(u)及u=φ(x)的单调性探求y=f[φ(x)]的单调性的一般方法.
3.3 指数函数(二)
答案
双基演练
1.③
2.0
4.{-1}
解析 解指数不等式<2x+1<4,得-1
5.(,+∞)
解析 ∵函数y=()x在R上为减函数,
∴2a+1>3-2a,∴a>.
6.-1
1.QP
解析 因为P={y|y≥0},Q={y|y>0},所以QP.
2.[0,4)
解析 ∵4x>0,∴0≤16-4x<16,
∴∈[0,4).
3.3
解析 函数y=ax在[0,1]上是单调的,最大值与最小值都在端点处取到,故有a0+a1=3,解得a=2,因此函数y=2ax-1=4x-1在[0,1]上是单调递增函数,当x=1时,ymax=3.
4.②
解析 f(-x)=3-x+3x=f(x),
g(-x)=3-x-3x=-g(x).
5.f(x)=-e-x-2
解析 ∵y=f(x)的图象与g(x)=ex+2的图象关于原点对称,
∴f(x)=-g(-x)=-(e-x+2)=-e-x-2.
6.c
∴b>a>1.又0
解析 假设第一天荷叶覆盖水面面积为1,则荷叶覆盖水面面积y与生长时间的函数关系为y=2x-1,当x=20时,长满水面,所以生长19天时,荷叶布满水面一半.
8.(-∞,-1)
解析 ∵f(x)是定义在R上的奇函数,
∴f(0)=0.
当x<0时,f(x)=-f(-x)=-(1-2x)=2x-1.
当x>0时,由1-2-x<-,()x>,得x∈ ;
当x=0时,f(0)=0<-不成立;
当x<0时,由2x-1<-,2x<2-1,得x<-1.
综上可知x∈(-∞,-1).
9.[1,+∞)
解析 利用复合函数同增异减的判断方法去判断.
令u=-x2+2x,则y=()u在u∈R上为减函数,问题转化为求u=-x2+2x的单调递减区间,即为x∈[1,+∞).
10.解 (1)设x1
(2)令u=x2-2x-1=(x-1)2-2,
则u在区间[1,+∞)上为增函数.
根据(1)可知y=在[1,+∞)上为增函数.
同理可得函数y在(-∞,1]上为单调减函数.
即函数y的增区间为[1,+∞),减区间为(-∞,1].
11.解 (1)∵t=2x在x∈[-,]上单调递增,
∴t∈[,].
(2)函数可化为:f(x)=g(t)=t2-2t+3,
g(t)在[,1]上递减,在[1,]上递增,
比较得g()
f(x)max=g()=5-2.
∴函数的值域为[2,5-2].
12.①
解析 当x→-∞时,2x→0,所以y=2x-x2→-∞,
所以排除③、④.
当x=3时,y=-1,所以排除②.
13.(1)解 ∵f(0)==0,
∴f[f(0)+4]=f(0+4)=f(4)==.
(2)证明 设x1,x2∈R且x1
∴f(x2)-f(x1)=
=>0,
即f(x1)
